Типы плоскостей скольжения

Типы плоскостей	Частичные трансляции
m	Чистая зеркальная плоскость
a	a/2
B	b/2
c	c/2
n	(a+b)/2,(a+c)/2,(b+c)/2
d	(a+b)/4,(a+c)/4,(b+c)/4

Б. Винтовая ось. Пусть R=C_n^z, а _R – частичная трансляция вдоль оси поворота (другой трансляции быть не может). Можно показать, что

,

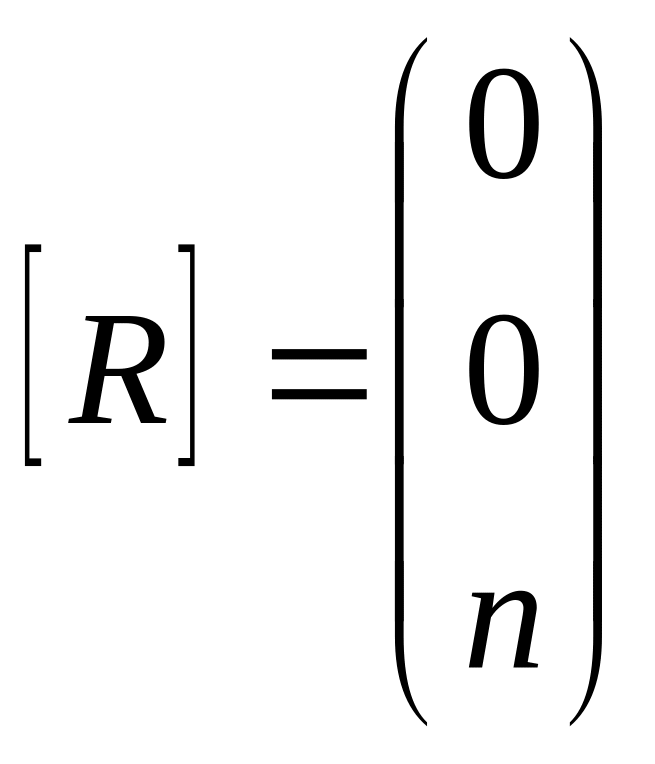а единственная компонента трансляции вдоль оси z должна иметь вид _R=(0,0,_R). Поэтому

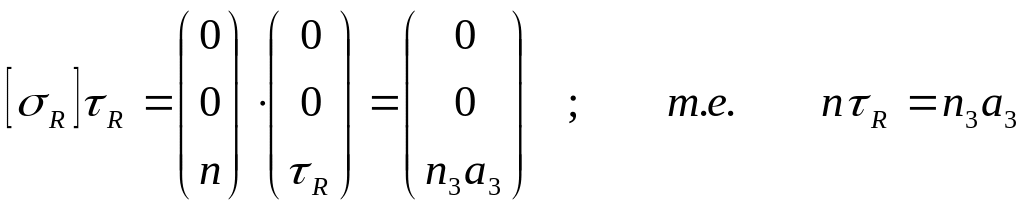
Величина n₃ может принимать значения меньше n. Например, для n=6 n₃=1,2,3,4,5 и вектора частичных трансляций _R для C₆ могут быть 1*а₃/6, 2*а₃/6, 3*а₃/6, 4*а₃/6, 5*а₃/6. Обозначения этих винтовых осей соответственно 6₁, 6_2, 6₃, 6₄ и 6₅ .

Аналогичные результаты получаются и для осей C₂, C₃ и C₄:

C₂:  2₁

C₃:  3₁ , 3₂

C₄:  4₁ , 4₂ , 4₃

C₆:  6₁ , 6₂ , 6₃ , 6₄ , 6₅

1.3. Сингонии и кристаллические классы

Проблема классификации кристаллических сред по симметрии состоит в том, чтобы найти такие группы {(R,t)}, в которых бы содержались указанные выше операции и которые были бы совместимы с пространственной периодичностью. Число таких групп 230. Из них 73 группы не содержат частичных трансляций; они называются симморфными.

Точечной группой решетки (голоэдрической группой) называют совокупность операций (R,0) первого и второго рода, совмещающих решетку саму с собой. Очевидным элементом такой группы является центр инверсии (поскольку всегда существуют вектора трансляций t_n и –t_n). Далее, если точечная группа решетки имеет ось симметрии C₂,то всегда имеется плоскость симметрии, перпендикулярная этой оси, т.е. существует группа C_2h; если имеется ось C_n (n=3,4,6), то точечная группа решетки содержит группу C_nv. Таким образом, для выяснения голоэдрических групп нужно составить список точечных групп, которые имеют:

• а) центр инверсии I;

• b) оси порядка 2,3,4 и 6 – C₂, C₃, C₄, C₆;

• c) плоскости отражения _h для C₂ и _v для C₃, C₄, C₆.

Этим условиям удовлетворяют 7 точечных групп, называемых кристаллическими системами (сингониями). См табл.2.

Таблица 2.

Кристаллические системы – сингонии

обозначение Шенфлиса	обозначение междуна-родное	Название кристаллической системы (сингония)	Решетки Браве
S2=Ci	1	триклинная	P
C2h	2/m	моноклинная	P, C
D2h	mmm	орторомбическая	P, C, F ,I
D3d	3/m	ромбоэдрическая (тригональная)	P
D4h	4/mmm	тетрагональная	P, C
D6h	6/mmm	гексагональная	P
Oh	m3m	кубическая	P, F, I

В каждой из семи кристаллических систем (точечных групп решетки) находится определенное число типов решеток, которые могут быть простыми (P), базоцентрированными (C), гранецентрированными (F), и объемоцентрированными (I). Поэтому полное количество решеток может быть равно 14 (решетки Браве). Вид элементарной ячейки и возможные типы решеток Браве перечислены ниже.

1. ТРИКЛИННАЯ – C_i. На углы и длины элементарных векторов трансляции не наложено никаких ограничений (из–за отсутствия элементов симметрии, кроме C_i). Решетка примитивная – P; 90^о и аbc.

2. МОНОКЛИННАЯ – C_2h. Есть C₂ и плоскость, перпендикулярная оси C₂. Таким образом, одна их трансляций может быть выбрана перпендикулярно двум другим. Поэтому 90^о, =90^о и аbc. Нетрудно видеть, однако, что ячейка этого типа может быть не только примитивной, т.е. атомы могут быть расположены не только в ее вершинах. Элементарная ячейка может быть примитивная – P и базоцентрированная – C. (Элементарной ячейкой называют ячейку, обладающую симметрией решетки и имеющую наименьший объем).

3. ОРТОРОМБИЧЕСКАЯ – D_2h. Все три элементарных вектора трансляции могут быть выбраны в соответствии с требованиями симметрии, т.е. вдоль ортогональных осей C₂ группы D_2h. ===90^о и аbc. Любая грань в элементарной ячейке в этой сингонии может иметь дополнительный узел. Поэтому ячейка может быть примитивной – P, базоцентрированной – C, объемоцентрированной – I, и гранецентрированной – F.

4. ТРИГОНАЛЬНАЯ – D_3d. ==90^о и а=b=c. Ячейка – P.

5. ТЕТРАГОНАЛЬНАЯ – D_4h. ===90^о и а=bc. Ячейка P и I.

6. ГЕКСАГОНАЛЬНАЯ – D_6h. ==90^о; =120^о и а=bc. Ячейка P.

7. КУБИЧЕСКАЯ – O_h. ===90^о и а=b=c. Ячейка P, I, F.

ФАКТОР–ГРУППА

Если H – инвариантная подгруппа G, то все элементы G можно получить так: G=H+X₂H+X₃H+....+X_gH. Каждое слагаемое в этой сумме можно рассматривать как элемент новой группы, называемой фактор–группой; обозначается она как G/H. Элементами фактор–группы являются смежные (правые или левые) классы по H: H, X₂H, X₃H ....X_gH. Произведение двух смежных классов также смежный класс:

(X_iH)(X_jH)=X_i(HX_j)H=X_iX_j(HH)=X_iX_jH=X_qH

Единичный элемент – H: H(X_iH)=(HX_i)H=X_iHH=X_iH.

Поскольку подгруппа трансляций T – инвариантная подгруппа пространственной группы G, для описания симметрии кристалла можно ввести понятие фактор–группы G/T :

G=T+(R₂,_R2)T+(R₃,_R3)T+(R₄,_R4)T+..+(R_g,_Rg)T

Так как величины трансляций _Ri весьма малы по сравнению с величинами, рассматриваемыми при изучении макроскопических свойств, все дело происходит так, как будто все элементы симметрии пересекаются в одной точке. Тогда операции симметрии E, R₂, R₃,....R_g образуют конечную группу, изоморфную фактор–группе, поскольку правила умножения элементов той и другой группы идентичны. Таким образом, фактор–группа изоморфна одной из точечных групп, совместимой с пространственной периодичностью кристалла. Такие точечные группы называются кристаллическим классом. Их существует всего 32. Они перечислены в таблице 3, которая получена простым перечислением возможных для кристалла точечных групп. В первой колонке таблицы дан общий вид возможных точечных групп, допустимых для периодической пространственной решетки, а во втором столбце перечислены возможные точечные группы.

Требования инвариантности решетки при поворотах и отражениях R накладывает ограничения на вектора элементарных трансляций a, b, c и углы , , . Возможно, как было установлено, только 7 кристаллических систем (сингоний) или 14 решеток Браве. Они также указаны в самой правой колонке таблицы. Кристаллическую структуру можно получить, если с каждой точкой решетки Браве связать группу атомов, называемую базисом. Если базис состоит только из одного атома (например, в узле решетки), то кристаллическая структура будет обладать высшей точечной группой симметрии, возможной для решетки (ибо атом предполагается сферически симметричным). Такие точечные группы – голоэдрические группы.

Распределение кристаллических классов по сингониям дано в таблице 4. В каждой сингонии указано количество симморфных групп, т.е. число пространственных групп, в которых присутствуют только операции баз частичных трансляций (чистые повороты и зеркальные отражения).

Таблица 3.

Возможные кристаллические классы, изоморфные фактор–группе

	Кристаллический класс	Число групп
Cn	C1, C2, C3, C4, C6	5 групп
Dn	D2, D3, D4, D6	4 группы
T	T	1 группа
O	O	1 группа
Cnh	C1ħ=Cs , C2h , C3ħ , C4h , C6h	5 групп
Cnv	C2v , C3v , C4v , C6v	4 группы
Dnh	D2h , D3h , D4h , D	4 группы
Dnd	D2h,, D3ħ	2 группы
Sn	S2=Ci , S4, S6=C3i	3 группы
Th	Th	1 группа
Td	Td	1 группа
Oh	Oh	1 группа
всего 32 группы

Если базис состоит не из одной молекулы и не обладает никакой симметрией, то можно ожидать, что кристалл будет принадлежать к триклинной сингонии и решетка относится к классу C₁, а пространственная группа является самой простой – примитивная решетка P и отсутствие элементов симметрии – такая пространственная группа обозначается C₁¹–P1. Если базис имеет центр инверсии, т.е. симметрию C_i , то структура будет относиться к триклинной сингонии, но кристаллический класс будет иметь центр инверсии (см. рис 3). Таким образом, кристаллический класс будет C_i, а пространственная группа C_i¹-P1. Итак, пространственная группа получается последовательным выбором одной кристаллической системы (сингонии), одного типа решетки Браве, одного типа кристаллического класса и одного типа частичных трансляций _R для каждого элемента симметрии. Итак,

Кристаллическая система – сингония – (7 типов)

