5. Многоатомная линейная цепочка

Линейная цепочка, состоящая из N элементарных ячеек размера a и имеющая в ячейке только один атом, при рассмотрении только продольных колебаний имеет N степеней свободы и столько же собственных частот. Эти частоты заданы дискретными значениями волновых векторов k=(2π/aN)p в зоне Бриллюэна, а p принимает значения от 1 до N–1. Линейная цепочка, в элементарной ячейке которой находится два атома, будет иметь в два раза больше степеней свободы и, следовательно, 2N значений собственных частот. Поскольку число возможных волновых векторов, а, значит, и колебаний (механических волн) с различными длинами волн λ всего N, решениями такой задачи должны быть две дисперсионные зависимости, заданные в области периодичности решений – в зоне Бриллюэна. В следующей главе будет показано, что одна из этих зависимостей выходит из начала координат и характеризует звуковые колебания, как это происходит в одноатомной цепочке, а другая – представляет собой дисперсионную зависимость, похожую на зависимость, реализующуюся в модели маятников, связанных упругими силами (см. рис. 13). В этом случае частоты возможных механических колебаний меняются от некоторой частоты ω(0) для бесконечно длинных волн (λ=∞, k=0) до другой частоты ω(π/a), принимающей эту величину при значении волнового вектора, равного k=π/a (λ=2a). В случае, когда число частиц в элементарной ячейке будет равно s, возникнет s функциональных зависимостей, заданных в первой зоне Бриллюэна и называемых ветвями. Таким образом, возникнет многозначная функция волнового вектора k, поскольку каждому значению волнового вектора будет соответствовать s частот, так что полное число частот будет равно Ns, что соответствует числу степеней свободы цепочки. При безграничном увеличении числа частиц, образующих элементарную ячейку, число ветвей также стремиться к бесконечности, так как оно равно числу степеней свободы ячейки. При этом цепочка переходит в непрерывную струну или стержень с макроскопических представлений с фактически отсутствующей периодической структурой.

Простейшем случаем такой системы может служить однородная непрерывная струна или стержень, не обладающие периодической структурой, т.е. макроскопические системы, рассматриваемые феноменологически. Если считать, что стержень имеет однородную структуру, и вдоль него распространяется акустическая волна, то частота колебаний ω является линейной функцией волнового вектора k. Переход от однородной непрерывной струны к струне с периодической структурой (например, к нагруженной струне) приводит к определенным особенностям, характерным для распространения волн различной природы в периодических средах.

6. Однородный упругий стержень и стержень с периодической плотностью

В частном случае идеальной упругой струны (или упругого стержня) уравнение колебаний выглядит следующим образом

+ .

Здесь C₁₁ – упругая постоянная, u – смещение элемента среды, а ρ – плотность среды. Дисперсионная зависимость в этом случае имеет вид =k(C₁₁/)^1/2, так что волны для нормальных мод однородной упругой струны – недисперсивны. Это означает, что последовательные моды идеальной струны (т.е. моды с длинами волн =2l/1, 2l/2, 2l/3, 2l/4... и т.д.) создают гармоническую последовательность частот: ₁ , ₂=2₁ , ₃₌3₁ и т.д.

Для реальной струны (например гитары или рояля) дисперсионное соотношение, вообще говоря, нелинейно и может быть приближенно описано формулой ²=(C₁₁/)k²+k⁴, где  – некоторая положительная константа, показывающая, что струна при возбуждении коротковолновых мод более жестка, чем при возбуждении длинноволновых. Поэтому частоты колебаний мод с длинами волн =2l/1, 2l/2.. и т.д. не будут удовлетворять гармонической последовательности ₁, ₂ =2₁, ₃ =3₁..., а будут несколько выше обертонов идеальной струны (т.е. будут диезными).

Можно рассмотреть струну с закрепленными на ней N грузами массой m, расположенными через равные интервалы a. Очевидно, что такая система представляет собой рассмотренный ранее случай одномерной моноатомной цепочки, так что дисперсионная зависимость для этой системы имеет вид (см. рис.10):

.

В этом выражении из-за дискретности системы (точечные массы, связанные невесомыми пружинами), механическая система имеет N частот, поскольку волновой вектор дискретен и принимает только N значений в зоне периодичности – зоне Бриллюэна. Таким образом, непрерывную (непериодическую) структуру можно рассматривать, как предельный случай периодических структур, в которой число образующих элементарную ячейку частиц N→∞ стремиться к бесконечности (рис. 15).

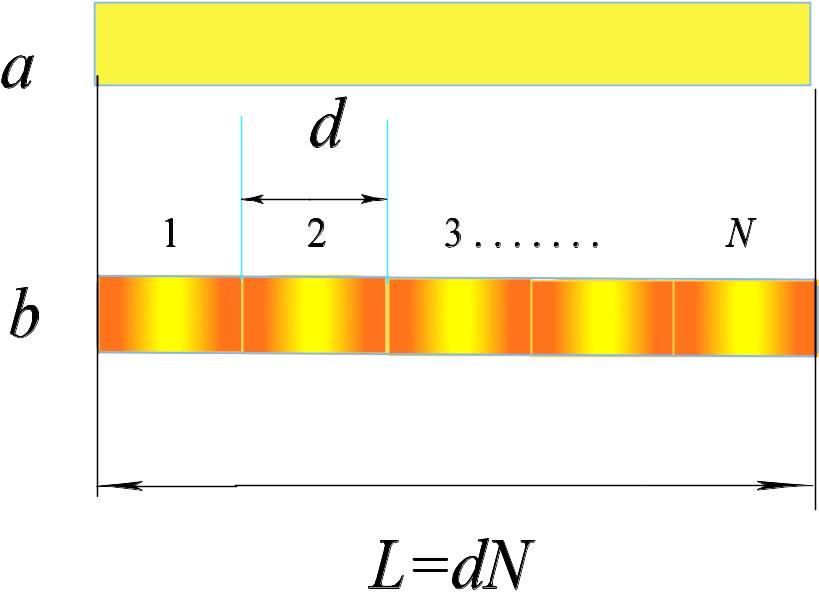
Рис. 15. Модель однородного стержня (а), для которого дисперсионная зависимость звука линейна, и модель стержня с периодической плотностью (б), для которого существуют области запрещенных частот для распространения звука (см. рис. 16).

Дисперсионная зависимость в этом случае линейна и существует для всевозможных волновых векторов. Однако непрерывную среду формально можно рассматривать как периодическую среду при бесконечно малых значениях периодического возмущения. В таком случае волновой вектор становится периодичным и охватывает только первую зону Бриллюэна, а дисперсионная зависимость будет иметь бесконечное число ветвей и станет многозначной. Если же область изменения k охватывает N зон, то функция ω(k) становится однозначной (рис. 16).

Рис. 16. Дисперсионная зависимость частоты звуковой волны в однородном стержне представляется наклонными прямыми с тангенсом наклона, равным скорости звука (нет дисперсии). В стержне, плотность которого периодически изменяется (см. рис.26), дисперсионная зависимость представляет собой деформированную прямую с разрывами в точках, определяемых периодом возмущений.

В стержне с периодически изменяемой плотностью (см. рис. 15), дисперсионная зависимость представляет собой деформированную прямую с разрывами в точках, определяемых периодом возмущений. При увеличении возмущения разрывы на линейной зависимости остаются на тех же местах, а величина разрыва увеличивается. Из-за периодичности решений по волновому вектору k удобно рассматривать такую дисперсионную зависимость в зоне периодичности от –π/d до +π/d, называемую первой зоной Бриллюэна. Дисперсионная зависимость будет иметь бесконечное число ветвей и станет многозначной.

Наличие периодического возмущения приводит к тому, что дисперсионная зависимость ω(k) становится разрывной вдоль линий, представляющих границы различных зон. При этих значениях волнового вектора, как известно, выполняется условие дифракции Лауэ, и последовательное Брегговское отражение от каждой из плоскостей вызывает отраженную волну, которая при движении в обратную сторону также испытывает отражения. Единственным стационарным состоянием в этой ситуации может быть стоячая волна, число полуволн которой точно укладывается в длину струны или стержня. С увеличением возмущения положение точек разрыва на дисперсионной кривой остается неизменным, а возрастает лишь величина разрыва функции ω(k). Сводя область изменения вектора k к первой зоне, получаем, что каждая зона высшего порядка соответствует одной из ветвей функции ω(k).