4. Фононы в идеальных кристаллах

Ранее было показано, что квантовомеханическая задача о собственных состояниях кристалла распадается на две задачи: электронную и ионную. Решение задачи ищется в виде  (R,r)=Ф(R,r)(R) (т.н. адиабатическое приближение), где Ф(R,r) – волновая функция, описывающая движение быстрых электронов в медленно меняющемся поле ядер, а (R) – волновая функция описывающая движение ядер в ядерном поле, создаваемом электронами. Поэтому в адиабатическом приближении движение электронов и атомных остатков может быть рассмотрено раздельно.

В настоящей главе будут рассмотрены собственные колебательные состояния кристалла. Однако, поскольку атомы кристалла велики (по сравнению с электронами) колебательную задачу можно рассматривать классически, т.е. рассматривать колебания точечных масс, связанных между собой квазиупругими силами (Борн, Карман, 1912).

Простейшим случаем такой задачи является линейная моно- или двухатомная цепочка, атомы которой могут совершать малые колеба­ния вблизи положения равновесия. Рентгеноструктурные данные (рис.18) показывают, что при не очень высоких температурах величина среднеквадратичного смещения атомов (u²)^1/2 значительно меньше межатомных расстояний в кристалле.22 случае кристалла GaN при 300^оC величина средне-квадратичного смещения атомов из положения равновесия может быть легко оценена из рис. 22.

[(u²)^1/2/a]=(0.1Å/1.96Å)5%.

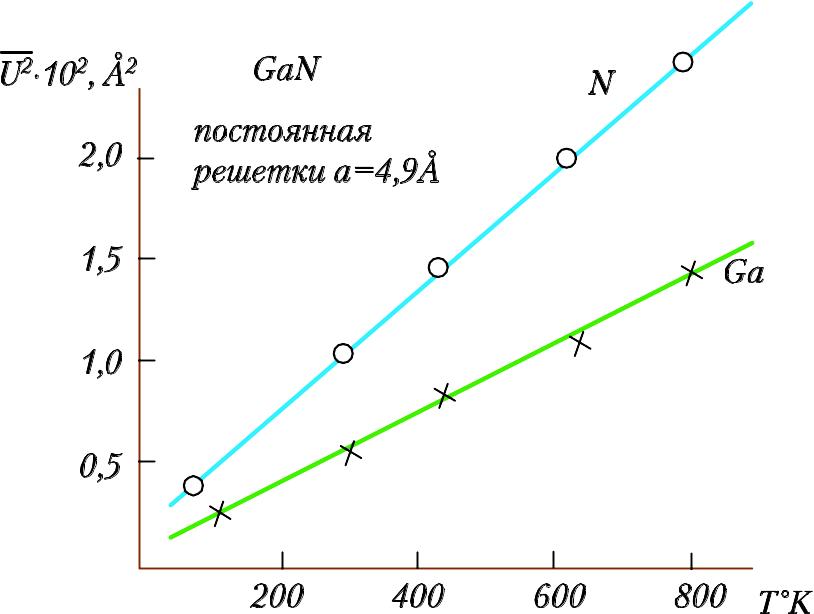
Рис. 22. Среднеквадратичные тепловые амплитуды (u²)^1/2 атомов галлия и азота в кристалле GaN.

Таким образом, приближение малых колебаний действительно может быть использовано, однако оно может оказаться неверным при температурах вблизи точки плавления кристалла.

4.1. Линейная двухатомная цепочка

Рассмотрим бесконечную одномерную цепочку, показанную на рис. 23, элементарная ячейка которой содержит 2 частицы. Трехмерным аналогом такой модели могут быть кристаллы NaCl, KBr и др. Постоянная решетки a=a′/2, a′–расстояние между соседними атомами, массы частиц – m₁>m₂, упругие силовые постоянны – ₁=₂=. Будем использовать четную нумерацию для частиц массы m₁ и нечетную – для частиц массы m₂. Соответствующие смещения u_2n и u_2n+1.

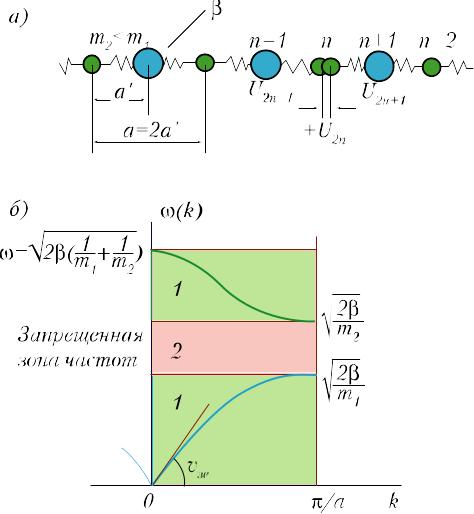
Рис. 23. Двухатомная линейная цепочка а) модель цепочки с массами m₁>m₂ и постоянной решетки a=2a′. На рисунке выделена элементарная ячейка. Тяжелые атомы решетки m₁ имеют нечетные номера, а более легкие атомы m₂ – четные; б) дисперсионная зависимость (k) для двухатомной линейной цепочки. 1 – дисперсивная область (зона собственных колебательных состояний); 2 – реактивная область (запрещенная зона частот). Дисперсионные зависимости (акустическая и оптическая ветви) непрерывны в зоне Бриллюэна и имеют экстремумы как в центре зоны (k=0), так и на ее границе (k=/a). В этом случае колебания цепочки представляют собой стоячую волну.

Система дифференциальных уравнений, описывающая движение частиц, имеет бесконечное число уравнений, имеющих для легкой и тяжелой частицы следующий вид:

.

Решение этой системы ищем в виде, удовлетворяющем теореме Блоха, т.е. в виде периодической функции, определенной в элементарной ячейке, домноженной на фазовый множитель expi(k,r_n).

,

где A₁ и A₂ – амплитуды смещений частиц массы m₁ и m₂,  – частота колебаний, а k – волновой вектор возбуждения.

Подстановка этих решений в бесконечную систему дифференциальных уравнений приводит eё к однородной системе из двух алгебраических уравнений относительно неизвестных амплитуд колебаний А₁ и А₂.

A₁(m₁²–2)+A₂2coska′=0

A₁2coska′+A₂(m2²–2)=0.

Чтобы система имела нетривиальное (ненулевое) решение, необходимо, чтобы ее детерминант равнялся нулю. Это дает связь между частотой возбуждения  и волновым вектором k, которая, как известно, носит название дисперсионного соотношения:

.

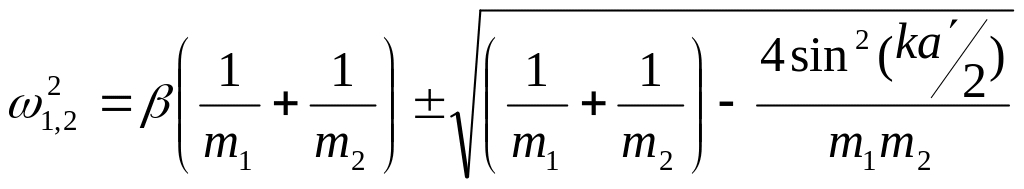Поскольку 1–2sin²ka′=coska, дисперсионное соотношение можно записать так:

.

Если частота  удовлетворяет дисперсионному уравнению, можно найти соотношение амплитуд А₁ и А₂ соответствующих волновых возбуждений, а из начальных условий можно найти и сам амплитуды. Поскольку дисперсионное условие имеет два корня ₁, ₂ каждому значению волнового вектора k соответствует две волны. В зависимости от k возбуждения цепочки имеют целый набор частот – ветвь (рис. 23).

Таким образом, дисперсионная кривая имеет две ветви – акустическую (знак –) и оптическую (знак +). Так как дисперсионная зависимость (k) периодична по k с периодом 2/a, нет необходимости рассматривать все возможные значения k. Область изменения волнового вектора k выбирается симметричной (–/a, +/a ), чтобы учесть волны, бегущие в противоположных направлениях. Эта область носит название первой зоны Бриллюэна.

Легко получить значения частот при k=0 и на границе зоны Бриллюэна (k=/a):

	центр зоны Бриллюэна	граница зоны Бриллюэна
Акустическая ветвь	a=0	а=(2/m1)1/2
Oптическая ветвь	о=(2(1/m1+1/m2))1/2	o=(2/m2)1/2

Внутри зоны ветви непрерывны. Ход ветвей вблизи центра зоны Бриллюэна при k0 можно получить, рассматривая разложение дисперсионной зависимости (k) в ряд по k, и учитывая, что сoska 1–k²a²/2+...:

1. Акустическая ветвь (знак –):

.

Скорость этой волны является скоростью звука, поскольку:

.

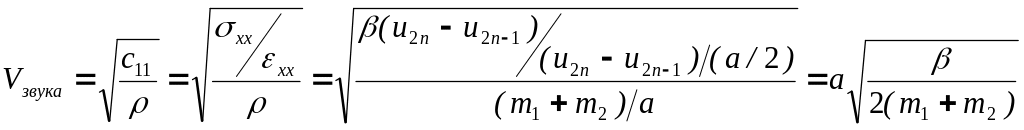2. Оптическая ветвь (знак +):

.

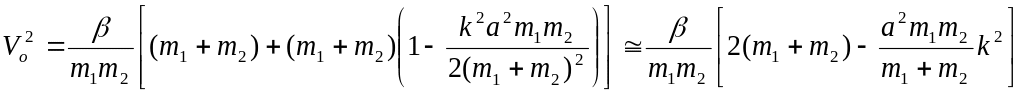Оптическая ветвь, таким образом, имеет максимум при k=0, а вблизи центра зоны Бриллюэна имеет параболическую зависимость от волнового вектора.

Ход ветвей на границе зоны Бриллюэна (k=/a) также можно получить, разлагая (k) в ряд в этой точке и учитывая, что

сoska  сos(–)=–сos =–1+²/2+... .,

для акустической и оптической ветвей имеем:

1. Акустическая ветвь (знак –):

.

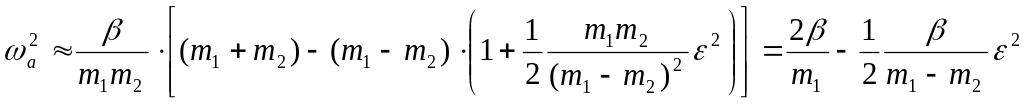Групповая скорость волны равна V_гр=(d/dk)_k=0=0 , т.е. это – стоячая волна.

2. Оптическая ветвь (знак + ):

.

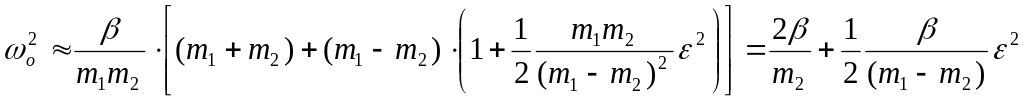Таким образом, частоты акустической и оптической ветви вблизи границы зоны Бриллюэна меняются по параболическому закону, а групповая скорость волны на границе зоны Бриллюэна равна нулю, т.е. это – стоячая волна.

Если ограничиться взаимодействием лишь ближайших соседей, то ветви внутри зоны гладки. Обе ветви идут, не пересекая друг друга, и имеет место область запрещенных частот от значения (2/m₁)^1/2 до (2/m₂)^1/2.

Характер движения частиц в ветвях можно получить, вернувшись к алгебраическим уравнениям для амплитуд А₁ и А₂. Если А₁/А₂>0, то движения частиц происходит в фазе, если А₁/А₂0 – в противофазе. Используя второе уравнение для амплитуд для нулевого волнового вектора, можно получить:

.

В акустической ветви (знак плюс) это отношение равно +1:

(А₁/А₂)_ak=(m₁–m₂+m₁+m₂)/2m₁=+1 ,

т.е. частицы с массами m₁ и m₂ движутся в фазе.

В оптической ветви (знак минус) это отношение отрицательно:

(А₁/А₂)_opt=(m₁–m₂–m₁–m₂)/2m₁= –m₂/m₁,

т.е. частицы колеблются в противофазе, а амплитуды движений обратно пропорциональны массам. Важно, что если на частицах 1 и 2 есть заряды, то такое колебание сопровождается изменением дипольного момента элементарной ячейки и, значит, оно может взаимодействовать со светом. Поэтому ветвь таких колебаний называется оптической.

В случае малых волновых векторов можно получить, что для акустической и оптической ветвей справедливо:

(А₁/А₂)_ak=1+k²;

(А₁/А₂)_opt= –(m₂/m1)(1–k² ),

где  = (m₁–m₂)/8(m₁+m₂).

В акустических колебаниях отношение амплитуд возрастает, а в оптических – уменьшается, но колебания тяжелых и легких частиц остаются в противофазе. Вблизи границы зоны Бриллюэна при k=(–)/a, coska –1+²/2+…, и отношения амплитуд имеет вид:

,

.

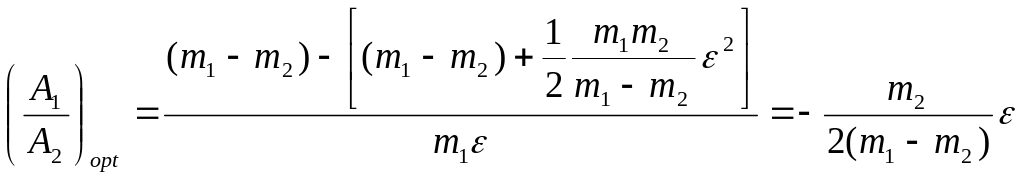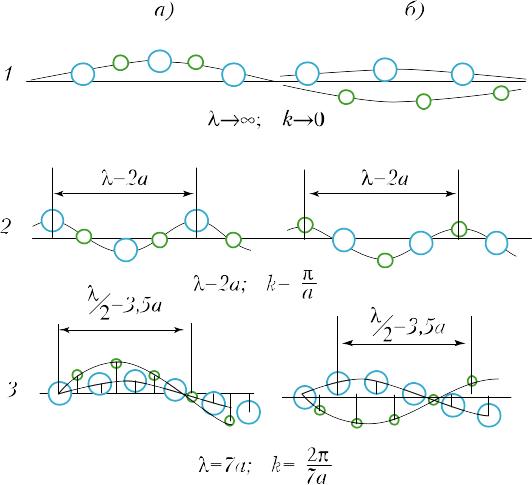
Рис. 24. Вид акустических (a) и оптических (б) колебаний двухатомной цепочки для значений волновых векторов k=0 (1), k=/a (2) и волнового вектора внутри зоны Бриллюэна k=/7a (3). Колебания с волновым вектором k=/a на границе зоны Бриллюэна представляют собой стоячие волны. В акустической ветви колеблются тяжелые атомы, а легкие покоятся; в оптической ветви колеблются легкие атомы, а тяжелые находятся в покое.

Поскольку в цепочке m₁–m₂>0, в колебаниях оптической ветви движения происходят в противофазе, причем при 0 (А₁/А₂)_opt0, т.е. тяжелые частицы покоятся, а легкие движутся. Длина волны при этом минимальна и равна =2a. В акустической ветви при колебаниях на границе зоны частицы движутся в фазе. При уменьшении  отношение (А₁/А₂)_ak возрастает и при 0 стремится к бесконечности. Это означает, что легкие частицы покоятся, а тяжелые движутся. Вид этих колебаний приведен на рис.24.

Для цепочки конечных размеров можно использовать циклические граничные условия Борна–Кармана, устанавливающие идентичность атома n и n+N:

u_n=u_n+N; exp[i(t+2nka′)]=exp[i(t+(2n+N)ka′)]

exp[iNka′]=1; Nka′=2p; p=0,1,2...N–1;

–/a<k=p2/Na<+/a; –N/2<p<+N/2

Таким образом, имеется N различных волновых векторов k, причем каждому волновому вектору k соответствует два колебания с частотами _ak и _opt, так что полное число типов движений ограничено и равно 2N (N – для оптической ветви и N – для акустической).

Трансформация ветвей в зоне при изменении периода решетки показана на рис. 25. На этом рисунке под знаком а) нарисована ветвь одноатомной цепочки с периодом a и одним атомом массы m в элементарной ячейке (сплошная кривая). В случае неконгруэнтности (отсутствия трансляционной инвариантности) атомов (m₁m₂) она переходит в две ветви типа А (акустическая) и О (оптическая). Поскольку элементарная ячейка в этом случае должна имеет удвоенный размер a′=2a, частоты обоих ветвей на границе зоны почти равны =/m₁  =/m₂ . В этом случае говорят, что зона Бриллюэна складывается в направлении k_. Трехмерный аналог этого случая – кристаллы C, Si, Ge, в решетке которых 2 атома в элементарной ячейке, и в которых в направлении (100) LA и LO ветви вырождены в точке X зоны Бриллюэна (см. рис. 33). Складывание зоны Бриллюэна в случае двухатомной линейной цепочки показано на рис. 25б. Появление сверхструктуры с периодами a′=2a, a′′=4a и т.д. приводит к последующему уменьшению зоны Бриллюэна и увеличению числа частот в центре зоны с k=0. На рис. 25в нарисованы мягкие моды в линейной двухатомной цепочке: под номером 1 – равновесная конфигурация цепочки с постоянной a и массами m₁ и m₂; под номером 2 – оптическое колебание в этой цепочке с k=0. При «замораживании» смещений число частиц в ячейке не изменяется; оптическое и акустическое колебания двухатомной цепочки с волновым вектором k=/a, т.е. на границе зоны Бриллюэна показаны под номером 3 и 4. При «замораживании» этих колебаний (т.е. смещений) число частиц в элементарной ячейке удваивается; замороженная конфигурация акустической моды 4, приводящая к цепочке с элементарной ячейкой удвоенного размера показано под номером 5. Штриховкой показана не конгруэнтность атомов в новой ячейке. Смещения частиц в этой конфигурации полностью подобны смещениям в случае 4, но представляют теперь нормальное колебание с волновым вектором k=0. Случаи 4 и 5 иллюстрируют складывание зоны, показанной на рис.25б, и переход точки с k=/a в точку k=0 зоны Бриллюэна другой фазы.

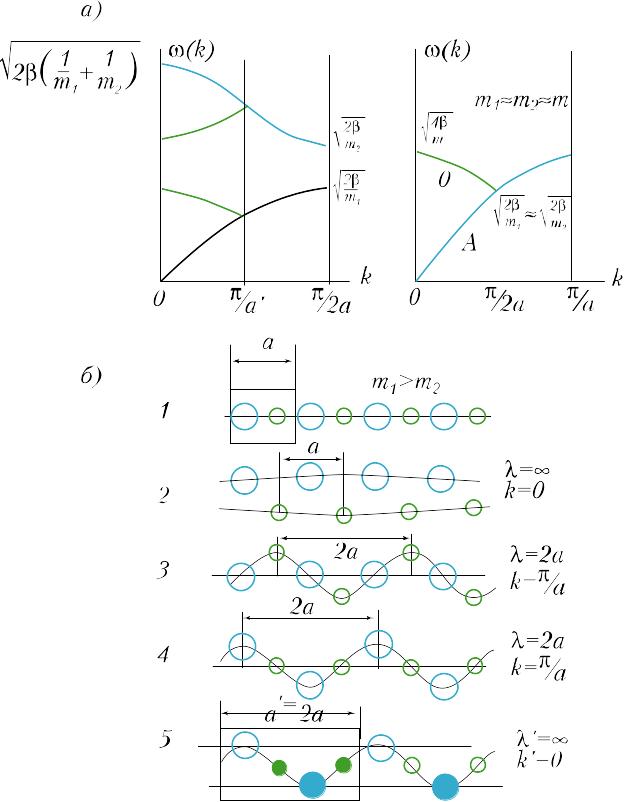
Рис. 25. Трансформация ветвей в зоне при изменении периода решетки.

Как и в случае одноатомной цепочки можно рассмотреть функцию плотности частот в ветвях g()=dZ/d, определяемую как число мод (типов колебаний) dZ, приходящихся на единичный интервал частот d. Ясно, что существует две области частот, где g() отличается от нуля. Эти области соответствуют акустической и оптической ветвям. Они разделены запрещенной областью частот, где g()=0. В граничных точках зоны Бриллюэна функция плотности частот стремиться к бесконечности, что является следствием приближения ближайших соседей. Полное число колебаний в цепочке конечно и равно 2N, так что

.

При рассмотрении реальной двухатомной цепочки необходимо учесть, что частицы могут смещаться не только вдоль цепочки, но и поперек, т.е. каждая частица будет иметь 3 степени свободы. Поэтому уравнений движения будет в 3 раза больше, и в 3 раза больше будет решений. Для каждого волнового вектора k будет существовать шесть волн с различными частотами, т.е. дисперсионная кривая будет иметь шесть ветвей. Три из них имеют частоты равные нулю при k0 (трансляционные движения частиц в фазе вдоль и поперек цепочки) и являются акустическими, остальные три – оптические.

В общем случае при наличии s частиц в элементарной ячейке полное число степеней свободы ячейки равно 3s. Полное число ветвей тогда будет 3s. Из них 3 ветви акустические, остальные 3s–3 ветви – оптические (рис. 26).

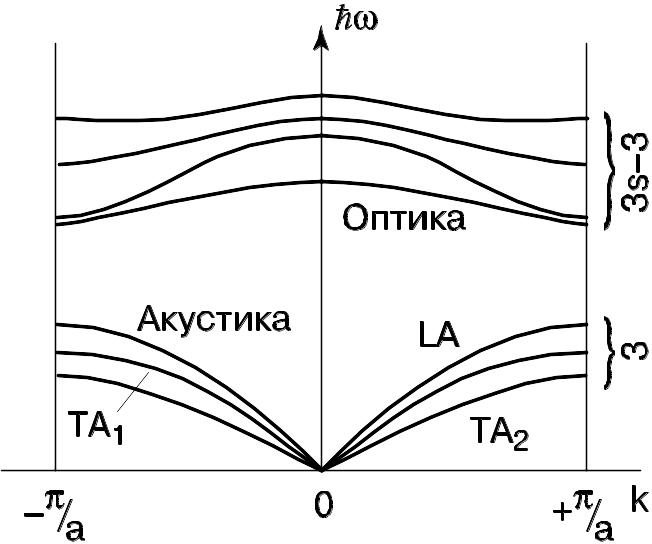
Рис. 26. Схематический вид дисперсионных зависимостей для кристалла с s атомами в элементарной ячейке для различных направлений k распространения волны.