4.6. Функция распределения плотности частот

В ряде термодинамических задач важно знать функцию распределения плотности частот g(). Функция g() – относительное число частот, заключенное в интервале частот от  до +d . Относительное число частот – это число частот, отнесенное ко всему числу частот кристалла 3N. Часто используют нормированную на единицу функцию плотности частот:

.

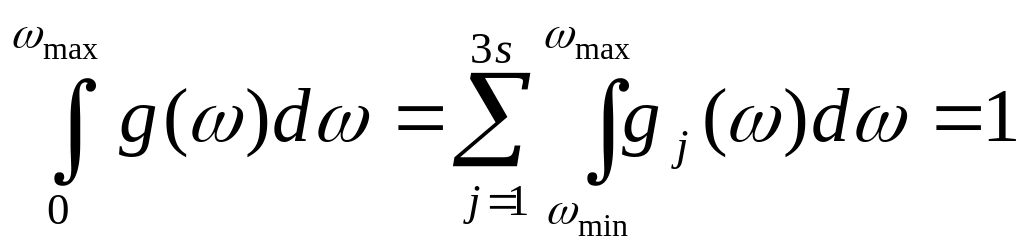Здесь g_j() – функция плотности частот в ветви j.

Единственный путь получить функцию распределения плотности частот - это решить вековое уравнение для всех точек зоны Бриллюэна, поскольку общих соотношений для функции g() не существует. Однако, для идеализированного случая изотропной и непрерывной среды получить функцию распределения плотности частот достаточно просто.

Предположим, что в такой среде существует предельная частота _max. Вследствие непрерывности среды и ее изотропности значение _max будет достигаться для одинаковых волновых векторов в любом направлении. Поэтому зона Бриллюэна в этом случае должна выглядеть сферой. Изочастотные поверхности в обратном пространстве (пространстве волновых векторов) также будут изображаться сферой. Поэтому число различных колебаний dN, заключеных между частотой  и +d будет пропорционально объему шарового слоя dN=4a²²d, а плотность частот равна:

.

Разумеется, модель можно усложнить и рассматривать распределение частот в каждой ветви. Однако для дискретной среды функция распределения плотности частот не имеет такого гладкого вида. Для простоты можно рассматривать лишь одну ветвь. Доля общего числа частот, лежащих в интервале от  до +d всегда будет пропорциональна объему обратного пространства, определяющего этот интервал частот:

где интеграл берется по объему слоя, для которого < _k < +d. Введем вектор

–

градиент частоты в k-пространстве. Он имеет размерность скорости и представляет собой групповую скорость пакета с волновым вектором k в среде, имеющей дисперсию. Используя эту величину, можно преобразовать выражение для плотности частот следующим образом. За элемент объема в k-пространстве возьмем цилиндр с образующей вдоль направления grad_k(k) и основанием, перпендикулярным этому направлению (т.е. на изочастотной поверхности (k)=const). Площадь основания цилиндра – dS_, а высота dk_N=d/grad_k(k). Поэтому функция плотности частот может быть представлена так:

.

Если в какой-либо точке grad_k(k)=0, то функция g() имеет особенность. В одномерном случае в этой точке (d/dk)=0, и плотность частот стремится к , хотя сама (k) может и не обращаться в  Такие точки обратного пространства носят название критических точек функции плотности состояний. Если вблизи такой точки дисперсионную зависимость (k) можно разложить в ряд Тейлора, то такие критические точки называются аналитическими критическими точками. Вблизи такой точки k_o можно написать:

.

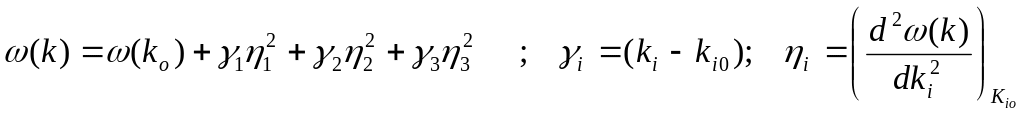Рассматриваемое разложение не содержит линейных членов по _i, поскольку grad_k(k)=0. В зависимости от числа I отрицательных знаков в совокупности коэффициентов ₁, ₂ и ₃ разложения (I – индекс критической точки или число Бетти) аналитические критические точки различаются следующим образом:

1. I=3, точка P₃ т.е._i <0 для всех I=1,2,3. (k) имеет локальный максимум, т.к. любое значение (k) меньше, чем значение функции в рассматриваемой точке (k_o). Поверхность постоянной частоты – эквипотенциальная поверхность (k) вблизи этой точки представляет собой эллипсоид с главными полуосями ₁, ₂, ₃. Объем обратного пространства, ограничиваемый такой поверхностью вблизи точки (k_o) равен:

.

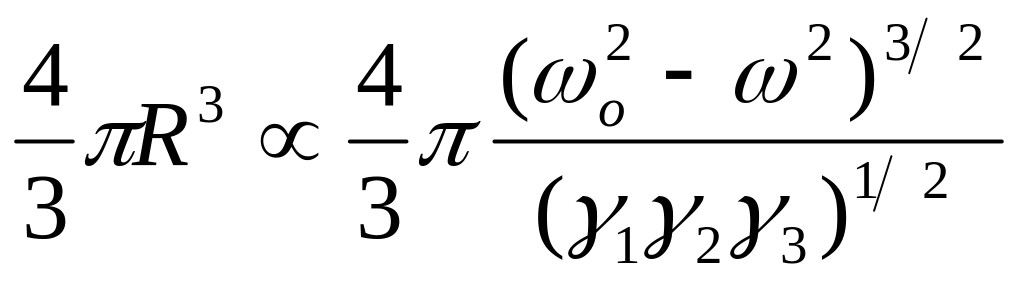Поэтому функция плотности частот в этом месте имеет особенность типа

.

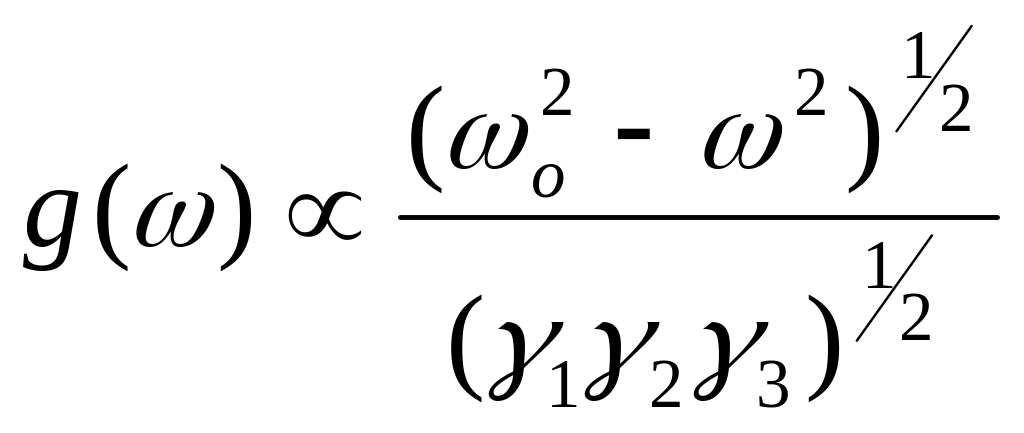g() в критической точке имеет конечное значение, однако производная dg()/d стремится к –, когда частота стремится к частоте в особой точке (k_o) со стороны меньших частот.

2. Число Бетти I=0, точка P₀, т.е. _i >0 для всех i=1,2,3. В этом случае дисперсионная функция (k) вблизи критической точки имеет локальный максимум, функция плотности частот имеет вид, аналогичный виду в минимуме, но dg()/d  + при _o со стороны высоких частот.

3. Если один из коэффициентов  >0, а два других меньше нуля, на дисперсионной зависимости в обратном пространстве возникает седловая точка, которая называется седловой точкой P₂ 2-го рода. Вблизи нее функция плотности частот ведет себя следующим образом:

.

4. Если один из коэффициентов _i разложения (k) больше нуля, а остальные два – меньше нуля, возникает седловая точка первого рода P₁. Вид функции плотности состояний в этом случае подобен седловой точке P₂ второго рода для  <_c. Поведение функции g() вблизи этих аналитических критических точек дано в табл.6.

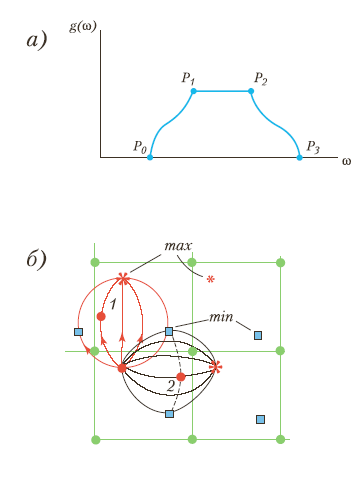
Рис. 34. Особенности Ван-Хова функции плотности состояний. а) Типы критических аналитических точек и особенности функции плотности состояний вблизи этих точек: P₀ – min функции (k), P₁ и P₂ – точки перегиба, P₃ – max функции (k). б) Топологическое обоснование особенностей плотности частот. Показаны кривые, соединяющие максимумы и минимумы периодической двумерной функции в обратном пространстве. Точки 1 и 2 – точки перегиба. Минимумы, находящиеся на сплошных кривых, соединяющих соседние максимумы, образуют геометрическое место точек, имеющих локальный максимум (пунктирная кривая). Одна из таких точек будет точкой перегиба. В элементарной ячейке обратного пространства в двумерном случае будет две таких точки. В трехмерной случае точки перегиба могут быть двух типов, и в зоне Бриллюэна помимо максимума и минимума функции (k) имеется по три точки перегиба каждого типа (теорема Ван-Хова).

Таблица 6.