3.3. Уравнение Матье и зонная структура

Распространение волн в сплошной среде с перио­дической структурой, приводит к появлению некоторых общих результатов, связанных с периодичностью решений по волновому вектору и, следовательно, к многозначности решений. Наиболее известным из этого круга задач является случай одномерной структуры, для которой уравнение распространения волны в упругой периодически промодулированной среде, показанной на рис. 15, выглядит так:

,

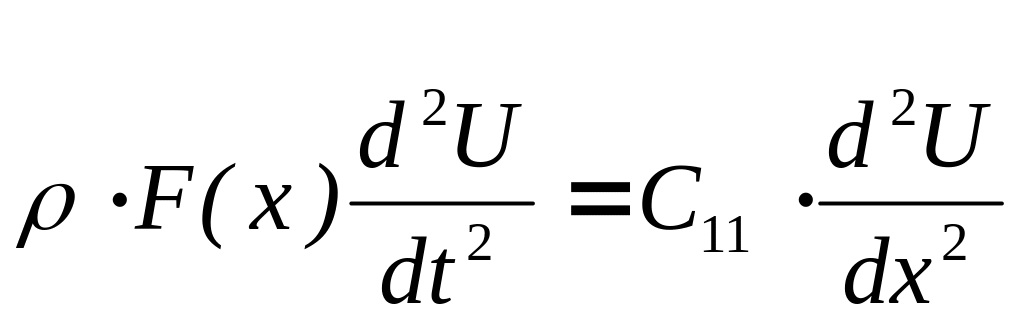где F(x) – некоторая периодическая функция, характеризующая либо периодическую модуляцию плотности ρ среды, либо ее упругих свойств C₁₁. Это уравнение, предполагая гармоническое его решение в виде U(x,t)=u(x)exp(it), можно свести к следующему уравнению:

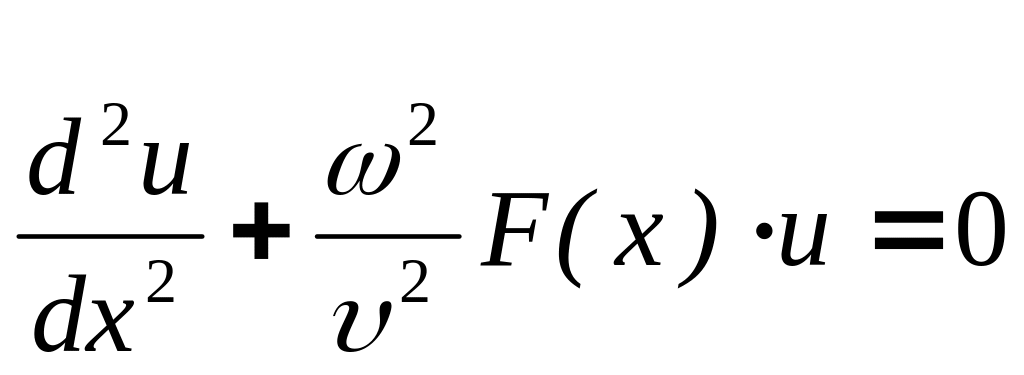, где – скорость звука в упругой среде.

Если предположить, что функция F(х) периодична по х с периодом d и состоит только из одного члена с косину­сом, то уравнение принимает форму уравнения Матье. При этих условиях разложение функция F(х) имеет вид:

F(x)=C₀+2C₁cos 2πx/d .

Предполагается, что периодическое возмущение мало, так что коэффициент С₁ очень мал и создает лишь малые поправки к упругим свойствам однородного стержня.

Уравнение Матье можно привести к каноническому виду, производя замену переменной

ξ= πx/d,

благодаря чему возмущающая функция будет иметь период не d, а π. Тогда получаем следующее уравнение для смещения и(ξ):

,

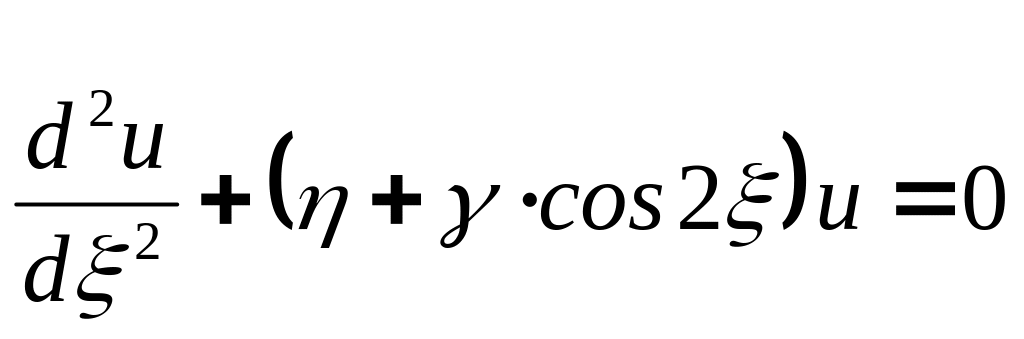где η = C₀ω²d²/²π² и γ = 2C₁ω²d²/²π².

Общее решение уравнения Матье имеет вид функции Блоха, поскольку речь идет о решении дифференциального уравнения второго порядка с периодическим потенциалом:

u(ξ) = D₁A(ξ) exp(iξ/π) + D₂B(ξ)exp(–iξ/π),

где D₁ и D₂ – некоторые постоянные, а A(ξ) и B(ξ) – периодические функции с периодом π. Учитывая существующий в решениях временной фактор exp(iωt), получаем, что решение для и(ξ) предста­вляет собой суперпозицию двух волн, распространяющихся в противоположных направлениях, одна из которых затухает, а другая нарастает.

Если рассматривать только одну из этих волн, то можно положить, что

u(ξ) = A(ξ)exp(iξ/π).

В этом случае предполагается, что решение существует только в виде волны, т.е. что по заданному показателю экспоненты , принимающему исключительно действительные значения, можно отыскать соответствующее значение частоты ω. Удобнее, однако, поступить наоборот: предполагая частоту заданной, можно определить характеристический показатель экспоненты . В этом случае показатель экспоненты может оказаться как мнимой, так и комплексной величиной, т.е. равным =k+i. Если  – действительная величина, то такое решение соответствует незатухающим гармоническим волнам. Если  – величина комплексная или чисто мнимая, то решение представляет собой затухающие волны.

Области, в которых появляются различные решения уравнения Матье, иллюстрируются на рис. 19, где по оси абсцисс отложена величина η= C₀ω²d²/²π² – аналог собственной частоты системы, а по оси ординат – величина γ=C₁ω²d²/²π², характеризующая значение периодического возмущения.

Заштрихованным (зеленым) областям соответствуют те пары значений γ и η, для которых величина  – действительное число k, т.е. затухание отсутствует. Остальным областям (красным), напротив, соответствуют те значения параметров η и γ, при которых параметр  чисто мнимый или комплексный, т.е. в этих областях волна затухает.

Применяя терминологию, принятую в физике твердого тела, можно сказать, что не заштрихованные области соответствуют запрещенным зонам (или зонам затухания), а заштрихованные — зонам свободного распространения волн (или зонам пропускания).

Плоскость η, γ на рис. 19 удобно разбить на три области, проведя прямые η=γ и η=–γ, которые удобно принять за новые координатные оси. При неограниченном возрастании η и при условии η>—γ заштрихованные области сужаются, превращаясь в пределе в прямые, параллельные направлению η=—γ. Любая прямая, параллельная оси η пересекает области, соответствующие распространения волн, и области, в которых волны затухают. При этом при увеличении параметра γ, характеризующего величину периодического возмущения, ширина запрещенной зоны быстро увеличивается. При всех η < — γ распространяющиеся волны существовать не могут.

На границах заштрихованных и не заштрихованных областей мнимая часть комплексного числа =k+i обращается в нуль, т.е. Im =0, или =0.

Ось параметра η, характеризующего частоту волн, соответствует значению параметра γ=0, что имеет место в случае однородной бесконечной среды без периодической модуляции структуры. Положительная полуось η проходит только через заштрихованные области, т.е. запрещенных зон в решении нет. В области, непосредственно прилегающей к оси η, даже при очень малых значениях γ<<η, что соответствует появлению бесконечно малых периодических возмущений, появляются запрещенные для распространения волн области. Две кривые, ограничивающие заштрихованные области, начинаются всегда в точках оси η с абсциссой η=n², где n – целое.

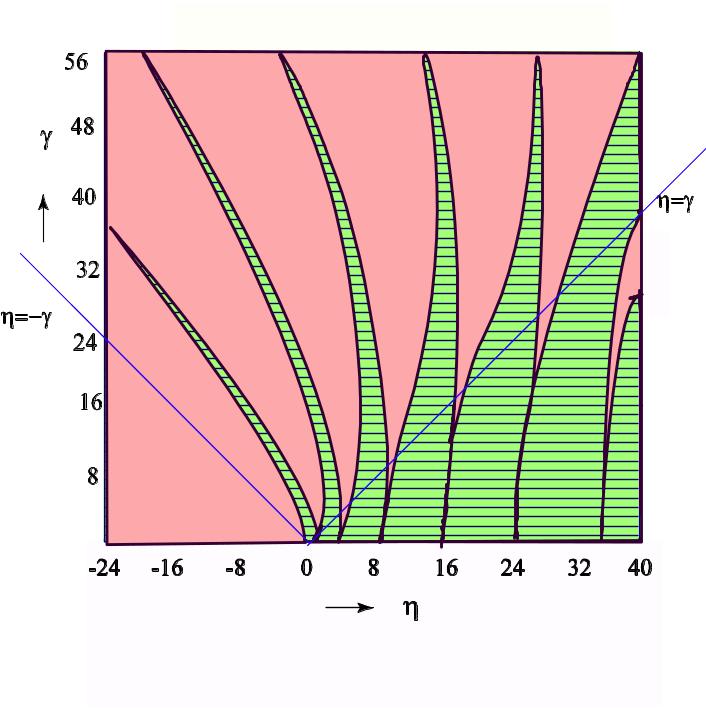
Рис. 19. Области мнимых (не заштрихованные, красные) и действительных (заштрихованные, заленые) значений экспоненциального показателя  решений уравнения Матье. В заштрихованных областях решение представляет собой незатухающие гармонические волны, которые свободно распространяются в периодически модулированном стержне. Не заштрихованные области рисунка соответствуют комплексным значениям показателя  и тем самым определяют затухающие волны в системе. Важно, что при отсутствии возмущения (γ=0) существуют только незатухающие собственные колебания. При любых, даже незначительных периодических возмущениям, появляются области, в которых существуют затухающие волны, т.е. появляются зоны запрещенных собственных колебаний системы. При росте возмущения запрещенные для распространения области увеличиваются.

На рис. 19 прямая, соответствующая постоянному отношению параметров η/γ=C₀/2C₁, определяет квадраты частот волн в стержне с постоянными значениями параметров C₀ и C₁. Пере­мещаясь вдоль этой прямой, можно последовательно попадать в области, соответствующие полосам непропускания или пропускания. Зависимость этой частоты от параметра  представлена на рис. 16, который был получен исключительно при качественном рассмотрении. На границах раздела этих областей параметр  действителен и равен k=π/d, что соответствует границам зон Бриллюэна.

Вместо того чтобы рассматривать, как это делается в слу­чае однородной невозмущенной среды, всю область изменения k, в которой определена непрерывная кривая ω(k)=v_звk, в случае возмущенной среды удобно ограничиться лишь значениями k, попадающими в первую зону Бриллюэна –π≤ kd≤ π. Все ветви разрывной кривой ω(k) тогда удобно перенести в эту область и рассматривать многозначную функцию ω(k). Отсюда получается следующий важный результат: если возмущение увеличивается, т. е. если С₁, растет, то положение разрывов не меняется, но величина этих разрывов возрастает.