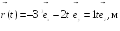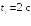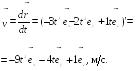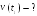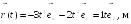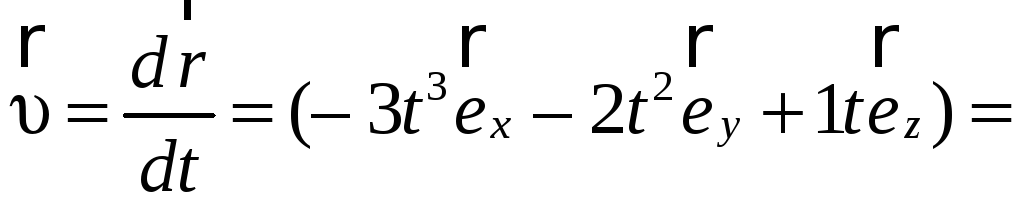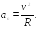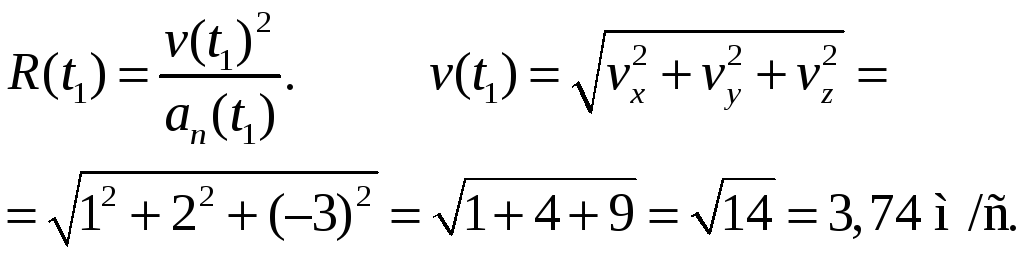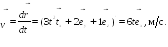- •Курс физики
- •Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
- •§ 2. Скорость и ускорение
- •§ 3. Сила и работа
- •Глава 2. Кинематика и динамика вращения твердого тела § 4. Угловая скорость и угловое ускорение
- •§ 5. Средняя скорость и среднее ускорение
- •§ 6. Момент силы
- •Глава 3. Законы сохранения § 7. Механическая энергия. Закон сохранения механической энергии
- •§ 8. Импульс. Закон сохранения импульса
- •§ 9. Момент импульса. Закон сохранения момента импульса
- •Глава 4. Механические колебания § 10. Гармонические колебания
- •§ 11. Затухающие колебания
- •§ 12. Вынужденные колебания
- •Глава 5. Механические волны § 13. Гармонические волны
- •§ 14. Плоская гармоническая волна
- •Экзаменационные вопросы 1
- •Контрольные задания 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение а
- •Молекулярная физика глава 6. Кинетическая теория газов § 15. Уравнение состояния идеального газа
- •§ 16. Внутренняя энергия идеального газа
- •§ 17. Распределение Максвелла
- •§ 18. Барометрическая формула
- •§ 19. Распределение Больцмана
- •§ 20. Явления переноса
- •Глава 7. Термодинамика § 21. Термодинамическая система и термодинамический процесс
- •§ 22. Первый закон термодинамики
- •§ 23. Теплоемкость идеального газа
- •§ 24. Адиабатический процесс
- •§ 25. Энтропия
- •§ 26. Второй и третий законы термодинамики
- •Глава 8. Реальные газы § 27. Силы межмолекулярного взаимодействия в газах
- •§ 28. Агрегатное состояние вещества
- •§ 29. Уравнение Ван-дер-Ваальса
- •§ 30. Внутренняя энергия реального газа
- •Экзаменационные вопросы 2
- •Контрольные задания 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Приложение б
- •Электромагнетизм глава 9. Электрическое поле в вакууме § 31. Напряженность поля
- •§ 32. Поток вектора
- •§ 33. Теорема Гаусса для поля вектора
- •§ 34. Циркуляция вектора
- •§ 35. Потенциал поля
- •§ 36. Связь между φ и
- •Глава 10. Электрическое поле в диэлектрике § 37. Диполь в электрическом поле
- •§ 38. Поляризация диэлектрика
- •§ 39. Вектор
- •Глава 11. Энергия электрического поля § 40. Электроемкость
- •§ 41. Электроемкость плоского конденсатора
- •§ 42. Энергия электрического поля
- •Глава 12. Электрический ток § 43. Электрический ток
- •§ 44. Закон Ома для проводника
- •§ 45. Обобщенный закон Ома
- •§ 46. Закон Джоуля – Ленца
- •Глава 13. Магнитное поле в вакууме § 47. Магнитная индукция
- •§ 48. Закон Био – Савара
- •§ 49. Теорема Гаусса для поля вектора
- •§ 50. Теорема о циркуляции вектора
- •§ 51. Магнитное поле в соленоиде
- •§ 52. Закон Ампера
- •Глава 14. Магнитное поле в веществе § 53. Контур с током в магнитном поле
- •§ 54. Намагничивание магнетика
- •§ 55. Вектор
- •Глава 15. Энергия магнитного поля § 56. Индуктивность
- •§ 57. Электромагнитная индукция
- •§ 58. Энергия магнитного поля
- •Глава 16. Электромагнитные волны § 59. Вихревое электрическое поле
- •§ 60. Ток смещения
- •§ 61. Система уравнений Максвелла
- •§ 62. Электромагнитные волны
- •Глава 17. Волновая оптика § 63. Свет
- •§ 64. Интерференция света
- •§ 65. Дифракция света
- •§ 66. Поглощение света
- •§ 67. Рассеяние света
- •§ 68. Поляризация света
- •§ 69. Закон Малюса
- •§ 70. Вращение плоскости поляризации
- •Контрольные задания 3 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 3
- •Приложение в
- •Квантовая физика глава 18. Квантовая оптика § 71. Тепловое излучение
- •§ 72. Закон Кирхгофа
- •§ 73. Законы теплового излучения черного тела
- •§ 74. Формула Планка
- •§ 75. Фотоэффект
- •§ 76. Формула Эйнштейна для фотоэффекта
- •§ 77. Фотон
- •§ 78. Эффект Комптона
- •Глава 19. Квантовая механика § 79. Волны де Бройля
- •§ 80. Волновая функция
- •§ 81. Соотношение неопределенностей Гейзенберга
- •§ 82. Уравнение Шредингера
- •§ 83. Микрочастица в потенциальном ящике
- •Глава 20. Атомная физика § 84. Атом водорода
- •§ 85. Излучение и поглощение света атомом водорода
- •§ 86. Пространственное квантование
- •§ 87. Принцип Паули
- •Глава 21. Зонная теория твердых тел § 88. Металлы, полупроводники и диэлектрики
- •§ 89. Электронно-дырочная проводимость полупроводников
- •§ 90. Примесные полупроводники
- •Глава 22. Ядерная физика § 92. Строение атомного ядра
- •§ 93. Энергия связи ядра
- •§ 94. Радиоактивность
- •Контрольные задания 4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Экзаменационные вопросы 4
- •Приложение г
- •Оглавление
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный университет
технологии и дизайна»
Ю. И. Соколов
Курс физики
Учебное пособие
Санкт-Петербург
2010
Механика глава 1. Кинематика и динамика частицы § 1. Путь и перемещение
М еханика
— это раздел
физики, в котором изучают механическое
движение — изменение положения тела в
пространстве с течением времени.
Положение тела в пространстве определяют
по отношению к другому телу, с которым
связывают систему координат, например,
декартову, представляющую собой три
взаимно перпендикулярные оси x,
y,
z
(рис. 1.1).
Система координат плюс часы для отсчета
времени образуют систему
отсчета.
еханика
— это раздел
физики, в котором изучают механическое
движение — изменение положения тела в
пространстве с течением времени.
Положение тела в пространстве определяют
по отношению к другому телу, с которым
связывают систему координат, например,
декартову, представляющую собой три
взаимно перпендикулярные оси x,
y,
z
(рис. 1.1).
Система координат плюс часы для отсчета
времени образуют систему
отсчета.
Рассмотрим кинематику движения тела, т. е. движение без учета его причины. Размерами движущегося тела будем пренебрегать и называть его просто частицей.
Положение
тела (частицы) в любой момент времени
![]()
![]() можно задать с помощью радиуса-вектора
можно задать с помощью радиуса-вектора
![]() ,
проведенного
из начала координат 0 в точку пространства,
в котором находится тело в момент времени
,
проведенного
из начала координат 0 в точку пространства,
в котором находится тело в момент времени
![]() (рис. 1.1).
Из рис. 1.1
видно, что радиус-вектор
(рис. 1.1).
Из рис. 1.1
видно, что радиус-вектор
![]() можно записать в виде
можно записать в виде
(![]() 1.1)
1.1)
где
![]() — координаты точки пространства,
— координаты точки пространства,
![]() ,
,![]() — орты системы координат — единичные
по модулю безразмерные векторы,
направленные по осям
— орты системы координат — единичные
по модулю безразмерные векторы,
направленные по осям
![]() соответственно.
соответственно.
Длина радиуса-вектора (его модуль)
(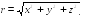 1.2)
1.2)
Очевидно,
при движении частицы ее радиус-вектор
меняется в общем случае как
![]() по
модулю, так и по направлению, т. е.
радиус-вектор зависит от времени
по
модулю, так и по направлению, т. е.
радиус-вектор зависит от времени
![]() :
:
![]() (1.3)
(1.3)
Если
известна зависимость
![]()
![]() ,
говорят, что задан закон
движения частицы.
,
говорят, что задан закон
движения частицы.
Линию,
описываемую частицей при ее движении,
называют траекторией
частицы
(рис. 1.2).
Пусть за промежуток времени
![]() частица переместилась вдоль траектории
из точки 1 в точку 2 (рис.
1.2) Проведем
из точки 1 в точку 2 вектор
частица переместилась вдоль траектории
из точки 1 в точку 2 (рис.
1.2) Проведем
из точки 1 в точку 2 вектор
![]() и назовем его перемещением
частицы за
промежуток времени
и назовем его перемещением
частицы за
промежуток времени
![]() Из рис. 1.2
видно, что
Из рис. 1.2
видно, что
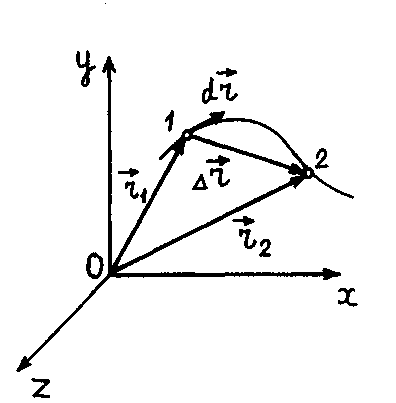
![]() (1.4)
(1.4)
приращению
радиуса-вектора
![]() частицы за промежуток времени
частицы за промежуток времени
![]() .
.
![]() С
учетом выражения (1.1) можем написать
С
учетом выражения (1.1) можем написать
![]()
Рис. 1.2
![]()
(1.5)
Элементарное
перемещение частицы из точки 1 за
элементарный (очень малый) промежуток
времени
![]()
![]() (1.6)
(1.6)
причем
нетрудно видеть, что вектор
![]() направлен по касательной к траектории
в точке 1.
направлен по касательной к траектории
в точке 1.
Назовем
длину отрезка траектории между точками
1 и 2 путем
S![]() ,
пройденным частицей за промежуток
времени
,
пройденным частицей за промежуток
времени
![]() Из рис. 1.2
видно, что обычно путь больше длины
(модуля) перемещения. Однако по мере
уменьшения пути это различие уменьшается.
Для элементарного (очень малого) пути
Из рис. 1.2
видно, что обычно путь больше длины
(модуля) перемещения. Однако по мере
уменьшения пути это различие уменьшается.
Для элементарного (очень малого) пути
![]() оно становиться ничтожным, что дает
право написать
оно становиться ничтожным, что дает
право написать
![]()
(1.7)
где
![]() — модуль элементарного перемещения
частицы.
— модуль элементарного перемещения
частицы.
§ 2. Скорость и ускорение
Мы
уже говорили, что при движении частицы
ее радиус-вектор меняется в общем случае
как по модулю, так и по направлению. В
кинематике вводят величину, характеризующую
быстроту изменения радиуса-вектора со
временем. Ее называют скоростью
![]() частицы.
частицы.
Пусть
в момент времени
![]() частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.1). За
элементарный (очень малый) промежуток
времени
частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.1). За
элементарный (очень малый) промежуток
времени
![]() радиус-вектор частицы получит элементарное
приращение
радиус-вектор частицы получит элементарное
приращение
![]() .
Векторную величину
.
Векторную величину![]()
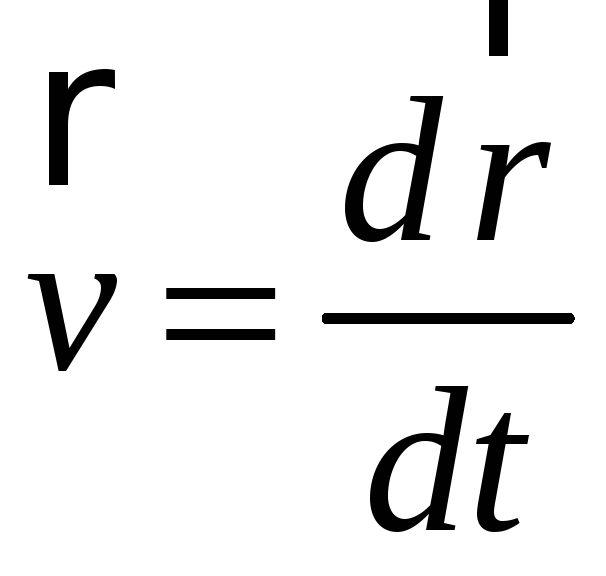 (2.1)
(2.1)
называют
скоростью частицы в точке 1 траектории.
Вектор
![]() направлен, так же как и вектор
направлен, так же как и вектор
![]() ,
по касательной к траектории в точке 1.
,
по касательной к траектории в точке 1.
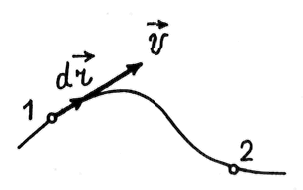
Рис. 2.1
Аналогично
определяют скорость частицы в любой
точке траектории или, что то же самое,
в любой момент времени
![]() движения частицы. В математике правую
часть равенства (2.1) называют производной
радиуса-вектора по времени. Следовательно,
скорость v
частицы в момент времени
движения частицы. В математике правую
часть равенства (2.1) называют производной
радиуса-вектора по времени. Следовательно,
скорость v
частицы в момент времени
![]() равна производной по времени от
радиуса-вектора этой частицы. Очевидно,
для определения скорости частицы в
любой момент времени надо знать закон
движения частицы (1.3).
равна производной по времени от
радиуса-вектора этой частицы. Очевидно,
для определения скорости частицы в
любой момент времени надо знать закон
движения частицы (1.3).
Можем написать
![]() (2.2)
(2.2)
где
![]() — проекции вектора
— проекции вектора
![]() на координатные
оси.
на координатные
оси.
Модуль скорости
![]() (2.3)
(2.3)
Принимая
во внимание соотношения (1.7) и (2.1), можем
записать выражение для элементарного
пути, проходимого частицей за элементарный
(очень малый) промежуток времени
![]() :
:
![]() (2.4)
(2.4)
где v — модуль скорости.
Чтобы
определить путь S![]() ,
проходимый частицей за промежуток
времени
,
проходимый частицей за промежуток
времени
![]()
![]() ,
надо просуммировать элементарные пути
,
надо просуммировать элементарные пути
![]() по длине отрезка траектории, проходимой
частицей за этот промежуток времени. В
математике такую операцию называют
интегрированием. Можем написать
по длине отрезка траектории, проходимой
частицей за этот промежуток времени. В
математике такую операцию называют
интегрированием. Можем написать
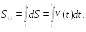
![]()
![]() (2.5)
(2.5)
Путь,
проходимый частицей за промежуток
времени
![]() равен
определенному интегралу от функции
v(t),
взятому в пределах от
равен
определенному интегралу от функции
v(t),
взятому в пределах от
![]() ,
до
,
до
![]() .
Очевидно,
чтобы произвести интегрирование (2.5),
надо знать зависимость модуля скорости
частицы от времени
.
Очевидно,
чтобы произвести интегрирование (2.5),
надо знать зависимость модуля скорости
частицы от времени
![]()
![]()
При
движении частицы ее скорость может
меняться как по модулю, так и по
направлению. В кинематике вводят
величину, характеризующую быстроту
изменения скорости со временем. Ее
называют ускорением
![]() частицы.
частицы.
Пусть
в момент времени
![]() частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.2).
частица, двигаясь по траектории,
находилась в точке 1 (рис.
2.2).
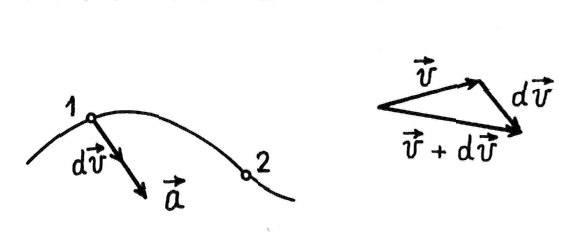
Рис. 2.2
За
элементарный (очень малый) промежуток
времени
![]()
![]() скорость частицы получит элементарное
приращение
скорость частицы получит элементарное
приращение
![]() .
Векторную величину
.
Векторную величину
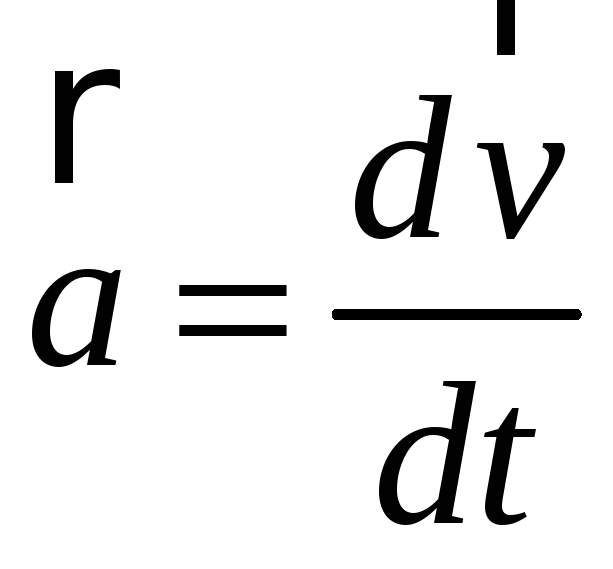 (2.6)
(2.6)
называют
ускорением частицы в точке 1 траектории.
Вектор
![]() направлен так же, как и вектор
направлен так же, как и вектор![]() .
.
Аналогично
определяют ускорение частицы в любой
точке траектории или, что то же самое,
в любой момент времени
![]() движения частицы. Ускорение
движения частицы. Ускорение
![]() частицы в момент времени
частицы в момент времени
![]() равно производной по времени от скорости
этой частицы.
равно производной по времени от скорости
этой частицы.
Очевидно,
зная закон движения частицы (1.3), можно
найти зависимость скорости
![]() от времени
от времени
![]() а
затем ускорение
а
затем ускорение
![]() в любой момент времени.
в любой момент времени.
Можем написать
![]() ,
(2.7)
,
(2.7)
![]()
где
![]() — проекции вектора
— проекции вектора
![]() на координатные оси.
на координатные оси.
Модуль ускорения
![]() (2.8)
(2.8)
Проведем
через некоторую точку траектории частицы
две оси: ось τ, направленную по касательной
к траектории в сторону вектора
![]() ,
и ось
,
и ось
![]() ,
направленную по нормали к траектории
к центру кривизны траектории в одной
точке (центру окружности, дугой которой
является элементарный (очень малый)
отрезок траектории частицы в районе
данной точки) (рис.
2.3). Тогда
вектор
,
направленную по нормали к траектории
к центру кривизны траектории в одной
точке (центру окружности, дугой которой
является элементарный (очень малый)
отрезок траектории частицы в районе
данной точки) (рис.
2.3). Тогда
вектор
![]() можно представить в виде суммы двух
составляющих
можно представить в виде суммы двух
составляющих
![]() и
и
![]() :
:
![]() ,
(2.9)
,
(2.9)
где
![]() и
и
![]() — орты осей
— орты осей
![]() и
и
![]() ;
;
![]() и
и
![]() — проекции векторов
— проекции векторов
![]() и
и
![]() на эти оси.
на эти оси.
![]() Вектор
Вектор
![]() называют
касательной
или
тангенциальным
ускорением,
вектор
называют
касательной
или
тангенциальным
ускорением,
вектор
![]() — нормальным
ускорением.
— нормальным
ускорением.
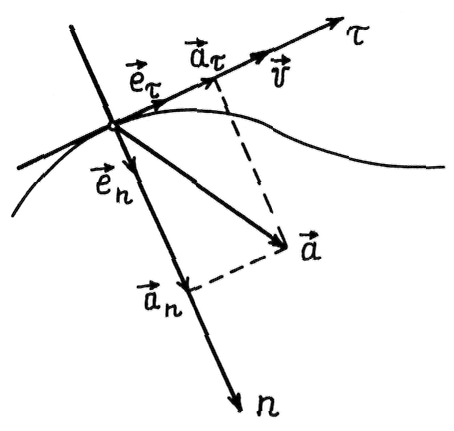
Рис. 2.3
Можно показать, что проекция
![]() (2.10)
(2.10)
производной
по времени от модуля скорости частицы.
Тангенциальное ускорение частицы
характеризует быстроту изменения модуля
ее скорости. При ускоренном движении
вектора
![]() совпадает с направлением скорости
совпадает с направлением скорости
![]() частицы. При замедленном движении вектор
частицы. При замедленном движении вектор
![]() противоположен направлению скорости
противоположен направлению скорости
![]() .
.
Можно показать, что проекция
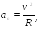
(2.11)
где
R
— радиус кривизны траектории в данной
точке. Нормальное ускорение характеризует
быстроту изменения направления скорости
частицы. Вектор
![]() всегда направлен к центру кривизны
траектории.
всегда направлен к центру кривизны
траектории.
Модуль ускорения
![]() .
(2.12)
.
(2.12)
Пример
2.1. Радиус-вектор
при движении частицы по траектории
изменяется по закону
![]() ,
м. Найти модуль
,
м. Найти модуль
![]() скорости частицы в момент t1
= 2с.
скорости частицы в момент t1
= 2с.![]()
![]()
|
Дано:
|
Решение
|
|
|
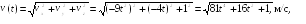
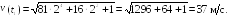
Ответ:![]()
Пример
2.2. Закон
движения частицы
![]() м. Найти проекцию
м. Найти проекцию
![]() ускорения частицы в момент времени t1
= 5c.
ускорения частицы в момент времени t1
= 5c.
|
Дано:
|
Решение
|
|
|
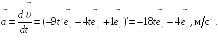
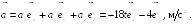
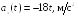 .
.
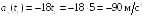 .
.
Ответ: ax(t1) = – 90 м/с2.
Пример
2.3. В момент
времени
![]() скорость частицы
скорость частицы
![]()
![]() ускорение
ускорение
![]() Найти радиус кривизны R
траектории в той точке, в которой частица
находится в момент времени
Найти радиус кривизны R
траектории в той точке, в которой частица
находится в момент времени
![]() .
.
|
Дано:
|
Решение
|
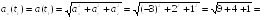
![]()
Ответ:
![]()
Пример
2.4. Закон
движения частицы
![]() Найти путь
Найти путь
![]() частицы
за одиннадцатую секунду ее движения.
частицы
за одиннадцатую секунду ее движения.
![]()
![]()
![]()
|
Дано:
|
Решение
|
|
|
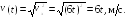
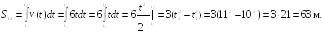
Ответ: S12 = 63 м.