1.13.2. Статистическое распределение выборки. Полигон. Гистограмма. Эмпирическая функция распределения

Статистическое распределение выборки – это соотношение между значениями вариант и соответствующими им частотамиили частостями (относительными частотами).

Статистическое распределение выборки можно представить в виде таблицы, в первую строку которой записываются варианты, а во вторую – соответствующие им частоты или частости

xi	x1	x2	…	xk
mi	m1	m2	…	mk
wi	w1	w2	…	wk

Здесь сумма всех частот равна объему выборки n, т.е.

,

а сумма частостей равна единице

.

Для непрерывного вариационного ряда составляется таблица, в первой строке которой указываются интервалы изменения вариант, а во второй – частоты.

хi	х1–х2	х2-х3	…
mi	m1	m2	…

Дискретные распределения можно представить полигоном, непрерывные – гистограммой.

Весь вариационный ряд с размахом разбивают на несколько интервалови подсчитывают число точек (частоту) на каждом интервале. Затем на каждом интервале строится прямоугольник, площадь которого равна относительной частоте интервала. Вся площадь гистограммы в этом случае равна единице.

Гистограмма Полигон

Эмпирической функцией распределения случайной величины Х называется функция

,

где m_x – число вариант, меньших х; n – объем выборки.

Эмпирическая функция распределения является оценкой функции распределения F(x)=P(X<х).

1.13.3. Статистические оценки параметров. Точность оценки, доверительная вероятность (надежность)

Выборку характеризуют такие показатели, как:

– среднее выборочное значение

(n – объем выборки);

– выборочная дисперсия

;

– центральные выборочные моменты

(все характеристики приведены для несгруппированных данных).

Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Несмещенной оценкой дисперсии будет исправленная выборочная дисперсия

.

При объеме выборки n > 30 можно использовать неисправленную выборочную дисперсию.

Среднее выборочное значение является точечной оценкой математического ожидания.

Если установить границы интервала , который с заданной вероятностьюР накрывает значение , то получиминтервальную оценку.

Пусть 1– обозначает вероятность того, что результат измерения отличается от истинного значенияm_x на величину, не большую . Это записывается так:

,

где 1– – доверительная вероятность (надежность) оценки; α – уровень значимости; () –доверительный интервал.

Величина  характеризует точность оценки математического ожидания и по абсолютной величине равна

,

где – среднее квадратическое отклонение;n – объем выборки.

Тогда предыдущую формулу можно переписать в виде

.

Величину 1– обычно выбирают 0,9; 0,95; 0,99.

Величину t_n находят по таблице распределения Стьюдента в зависимости от числа степеней свободы ν = n - 1 или объема выборки n и вероятности (уровня значимости) α [4, с. 217].

1.13.4. Метод моментов для точечной оценки параметров распределения

Метод предложен английским статистиком К.Пирсоном в 1895 г.

Его достоинство – чрезвычайная простота, особенно при небольшом числе параметров. Суть его сводится к приравниванию теоретических моментов, выраженных через параметры распределения, к эмпирическим.

Пусть задана плотность распределения с одним параметром, например, показательный закон

.

Требуется найти методом моментов точечную оценку параметра  по выборке t₁, t₂,…, t_n.

Решение. Выразим математическое ожидание через параметр 

.

Приравняем далее эмпирический и теоретический моменты , откуда.

Оценка двух параметров. Запишем нормальный закон распределения

.

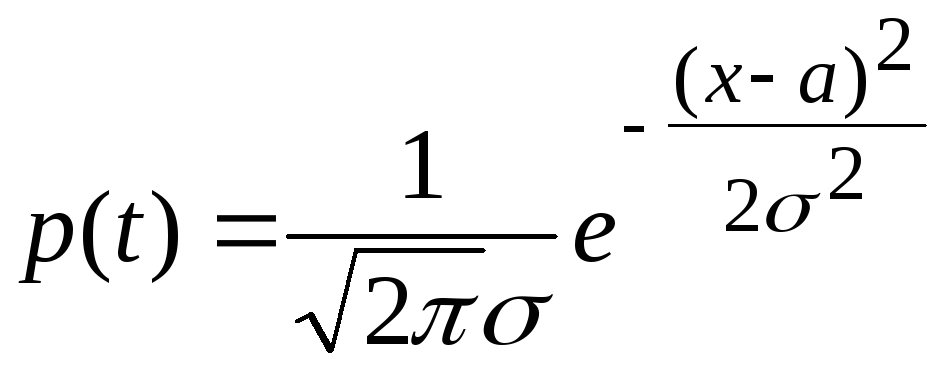Здесь .

По выборке t₁, t₂,…, t_n находим ии приравниваем теоретические моменты эмпирическим.

Следовательно, ;.

При бóльшем числе параметров необходимо составить r уравнений (по числу параметров) с r неизвестными и решить эту систему.