Обобщение систем непрерывных распределений по первому варианту на базе четырехпараметрической плотности p(t)

N п/п	Обобщающая функция	Параметр ε	при заданном ε	Система распределений
1				1
				2
2				2
				3
3				3
				4

3.6.2. Обобщение систем непрерывных распределений по второму варианту

В таблице 3.6.1 приведено три вида зависимостей между случайными величинами T и V. Чтобы получить новые зависимости, поменяем в этих формулах местами символы T, V и решим уравнения относительно Т. В результате найдем новые зависимости, которые приведены в табл. 3.6.2.

Таблица 3.6.2

Обобщение систем непрерывных распределений по второму варианту на базе четырехпараметрической плотности p(t)

N п/п	Обобщающая функция	Параметр ε	при заданном ε	Система распределений
1				2
				1
2				3
				2
3				4
				3

При двух значениях параметра ε (ε→0 и ε = 1) в функциях получаются четыре системы непрерывных распределений, заданные плотностямиp(v).

Найдем обобщенные пятипараметрические распределения на базе плотности p(t) и функций , приведенных в табл. 3.6.2.

Случай 1. Случайная величина T связана со случайной величиной V зависимостью [28] (см. табл. 3.6.2)

(3.6.7)

Тогда

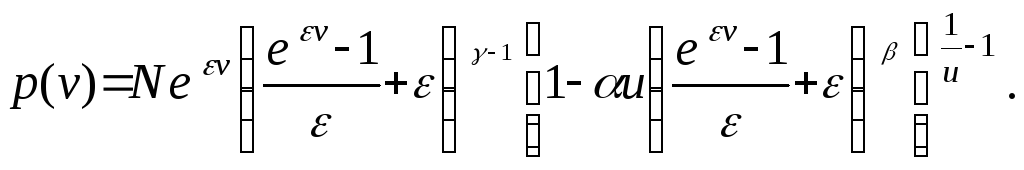(3.6.8)

Эта плотность обобщает вторую и первую системы непрерывных распределений. Из (3.6.8) при ε→0 следует вторая система непрерывных распределений, заданная плотностью (3.2.8)

Действительно, используя замечательный предел

из формулы (3.6.7) при ε→0 будем иметь

и, следовательно, плотность (3.6.8) принимает вид (3.2.8).

При ε = 1 и из формулы (3.6.8) следует первая система непрерывных распределений, заданная плотностью (3.4.3)

Случай 2. Случайная величина T связана со случайной величиной V зависимостью (см. табл.3.6.2)

(3.6.9)

Тогда

(3.6.10)

Эта плотность обобщает третью и вторую системы непрерывных распределений.

Из (3.6.10) при ε→0 следует третья система непрерывных распределений, заданная плотностью (3.4.4)

а при ε = 1 – вторая система непрерывных распределений, заданная плотностью (3.2.8) (см. случай 1).

Случай 3. Случайная величина T связана со случайной величиной V зависимостью (см. табл. 3.6.2)

(3.6.11)

Тогда

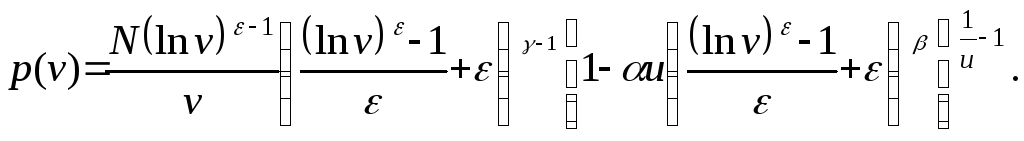(3.6.12)

Эта плотность обобщает четвертую и третью системы непрерывных распределений.

Из (3.6.12) при ε→0 следует четвертая система непрерывных распределений, заданная плотностью (3.5.5)

а при ε = 1 – третья система непрерывных распределений, заданная плотностью (3.4.4) (см. случай 2).

Итак, мы имеем набор четырехпараметрических систем непрерывных распределений (SNR1, SNR2, SNR3, SNR4) и множество промежуточных систем, т.е. от первой до четвертой системы имеется непрерывный ряд систем, но уже пятипараметрических с дополнительным параметром ε.

И, наконец, мы подошли к завершающему этапу построения обобщенных распределений.

Для того чтобы обобщенные плотности (3.6.8), (3.6.10), (3.6.12) включали как частные случаи дополнительные системы непрерывных распределений, в них необходимо добавить параметр сдвига l, т.е. представить в виде

(3.6.13)

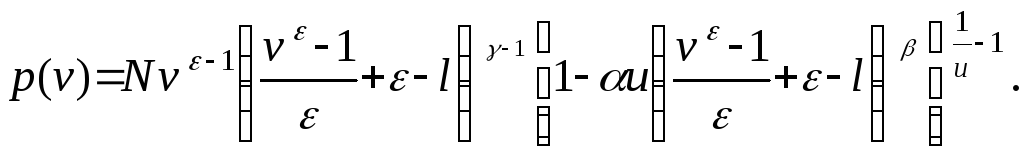(3.6.14)

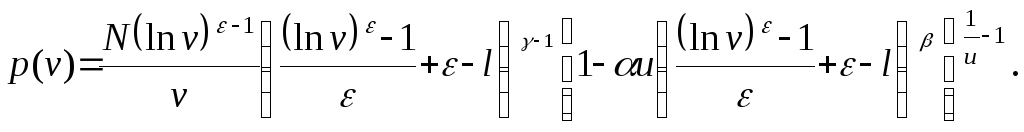(3.6.15)

В итоге получены три системы непрерывных распределений, заданные шестипараметрическими плотностями (3.6.13), (3.6.14), (3.6.15), и эти системы включают как частные случаи великое множество непрерывных распределений!

Напомним, что к этому результату привело обобщение всего лишь трех простейших непрерывных распределений и последние три формулы убедительно демонстрируют непостижимое волшебство метода обобщения!

Теперь можно быть уверенным, что с вероятностью близкой к единице среди этих распределений найдется подходящий частный случай для аппроксимации с достаточной точностью любого статистического распределения, если оно представляет собой однородную совокупность значений непрерывной случайной величины.

Построенные три системы непрерывных распределений открывают большой простор для новых исследований в области теории обобщенных распределений, в частности, для разработки более общих методов оценивания параметров.

Ниже будут рассматриваться в основном распределения, содержащие не более четырех параметров.