6.3. Оценивание параметров кривых роста

6.3.1. Уравнение прямой

Оценки параметров кривых роста вычисляются по методу наименьших квадратов. При этом уравнение кривой должно быть приведено к линейному виду

. (6.3.1)

Рассеяние отдельных значений случайной величины Х относительно прямой (6.3.1) должно описываться первой системой непрерывных распределений (SNR1), поскольку здесь последующие значения случайной величины Х_t+1 образуются из предыдущих Х_t путем прибавления постоянной величины В (см. свойства SNR1).

Если фактические уровни временного ряда Х_t получены как средние значения в моменты времени t (условные средние), то их рассеяние относительно прямой (6.3.1) может быть описано нормальным законом, который является частным случаем SNR1

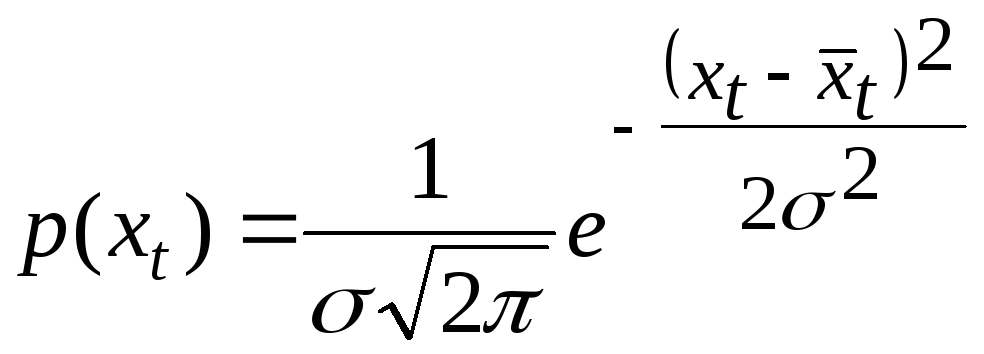
или с учетом (6.3.1)

. (6.3.2)

Плотность (6.3.2) представляет собой вариационно-дина­ми­ческую модель и содержит три параметра: А, В, σ. Их оценки можно найти по методу наибольшего правдоподобия. Для этого вначале прологарифмируем выражение (6.3.2)

и запишем логарифмическую функцию правдоподобия, представляющую собой математическое ожидание логарифма плотности распределения

.

Далее из условий

найдем уравнения правдоподобия:

Из первого уравнения имеем

.

Величина представляет собой остаточную дисперсию, несмещенная оценка которой равна

. (6.3.3)

Из второго и третьего уравнений путем замены соответствующих математических ожиданий их оценками получим систему двух уравнений с двумя неизвестными А, В:

Решение этой системы дает

(6.3.4)

. (6.3.5)

Сделаем некоторые выводы.

Оценки параметров А, В, полученные по методу наибольшего правдоподобия, совпадают с оценками метода наименьших квадратов. Оценка дисперсии совпадает с ее оценкой по методу моментов.

В качестве критерия точности выравнивания временного ряда может быть принят минимум остаточной дисперсии

или минимум суммы квадратов отклонений эмпирических значений уровней ряда от теоретической прямой

.

В этом случае коэффициент корреляции по модулю должен быть максимальным.

Полученные результаты позволяют оценить нижнюю и верхнюю границы уровня временного ряда при заданной доверительной вероятности Р

, (6.3.6)

где величина Z зависит от доверительной вероятности Р и числа степеней свободы ν, которое связано с числом точек n. При малых n величина Z определяется по таблицам распределения Стьюдента.

При Р = 0,9 величину Z можно рассчитать по формуле [24, с. 147]

, (6.3.7)

которая получена путем выравнивания табличных данных по формуле (6.2.3) с помощью соответствующей программы автора.

Произведение ZS является показателем точности аппроксимации при заданной надежности (доверительной вероятности) Р.

6.3.2. Экспонента

Рассмотрим еще пример, когда среднее логарифма случайной величины Y_t , т.е. растет во времени по линейному закону,

, (6.3.8)

а сама случайная величина Y_t (точнее, ее среднее геометрическое ) – по показательному закону.

В этом случае рассеяние отдельных значений случайной величины Y относительно экспоненты при каждом значении t должно описываться второй системой непрерывных распределений (см. свойства SNR2), а в частном случае – логарифмически нормальным законом

,

или с учетом (6.3.8)

. (6.3.9)

Оценки параметров А, В, σ распределения (6.3.9) легко находятся по методу наибольшего правдоподобия:

(6.3.10)

(6.3.11)

, (6.3.12) где S² – оценка дисперсии σ².

Нижняя и верхняя границы при заданной доверительной вероятности Р определятся по формулам

(6.3.13)