2.2. Математическое ожидание случайной функции и кривая роста новых событий. Связь с законами распределения вероятностей разных и новых событий

Рассмотрим полную группу попарно несовместных событий А₁, А₂,…, А_к ,…, А_n, вероятности которых заданы и соответственно равны p₁, p₂,…, p_к ,…, p_n. Пусть производятся независимые испытания, в каждом из которых может появиться одно из n разных событий, например, событие А_к.. При этом вероятность появления события А_к в любом испытании постоянна и равна р_к. Порядковый номер испытания обозначим через i (i = I, 2,…, Х+1).

Найдём вероятность того, что событие A_k появится первый раз в i-ом испытании и, следовательно, не появится во всех предыдущих (i-1)-ом испытаниях. Поскольку любое событие при первом его появлении от начала испытаний считается новым (обозначим его через ), то поставленную задачу можно сформулировать ещё так: найдём вероятность появления нового событиявi-ом испытании - Р_i(). По правилу умножения вероятностей независимых событий она будет равна

(2.2.1)

Рассмотрим далее новое событие – А^н, представляющее собой сумму n новых несовместных событий и найдём вероятность появления этого нового события вi-ом испытании. По правилу сложения вероятностей несовместных событий с учетом (2.2. I) имеем

(2.2. 2)

Рассмотрим теперь случайную величину Z_i - число появлений нового события А^н в i-ом испытании. Она может принимать только два значения: Z_i=1 (новое событие А^н наступило) с вероятностью Р_i(А^н) и Z_i=0 (новое событие не наступило) с вероятностью 1-Р_i(А^н). Математическое ожидание случайной величины Z_i равно вероятности появления нового события в i -ом испытании

Тогда математическое ожидание числа новых событий, наступающих при Х испытаниях, на основании теоремы сложения математических ожиданий будет равно сумме

или с учётом (2.2.2)

Суммируя вначале по i, затем по к, найдём

. (2.2.3)

Формула (2.2.3) ранее была получена В.М.Калининым [6, c. 246]. Она имеет смысл при целых значениях Х. В прямоугольных координатах

(Х; М[Y(X)]) каждому Х (Х = I, 2,…) соответствует ордината М[Y(X)]. Если соединить вершины ординат отрезками прямых, то получим ломаную, которую условимся также обозначать . При этом вероятность появления нового событияв(Х+1)-ом испытании равна тангенсу угла наклона (Х+1)-го отрезка ломаной к оси0Х

(2.2.4)

Из формулы (2.2.3) следует, что для нахождения математического ожидания случайной функции необходимо и достаточно знать вероятности всех n событий, составляющих полную группу. При этом разные события могут быть упорядочены по любому правилу. Следовательно, эта формула не позволяет решать весьма важную обратную задачу – по известному математическому ожиданию случайной функции находить закон распределения вероятностей n событий, составляющих полную группу. Для решения этой задачи необходимо иметь такую форму закона распределения, при которой он однозначно определялся бы математическим ожиданием случайной функции. Как показали исследования, такой формой закона распределения является распределение вероятностей новых событий. Выразим его через порядковый номер испытания i.

Обозначим через среднее значение вероятностей новых событий, которые могут наступить при одномi -ом испытании. Оно будет равно сумме произведений всех возможных значений вероятностей новых событий в i - ом испытании на вероятности p_к, т.е.

что с учётом (2.2.1) даёт

(2.2.5)

Формула (2.2.5) задаёт закон распределения длительности интервалов до наступления нового события.

Тогда накопленная вероятность новых событий, наступивших при Х испытаниях (другими словами - функция распределения вероятностей новых событий), будет равна сумме средних вероятностей

Суммируя по i, найдём

(2.2.6)

или, на основании равенства (2.2.4),

. (2.2.6')

Отметим, что формула (2.2.3) весьма неудобна как для теоретических исследователей, так и для практических расчётов, особенно при больших значениях n или X. В связи с этим математическое ожидание случайной функции (2.2.3) целесообразно аппроксимировать непрерывной плавной кривой, т.е. кривой роста новых событий. Найдем аналитическое выражение для этой кривой.

Будем считать, что события, составляющие полную группу, упорядочены по какому-нибудь правилу, например, по убыванию их вероятностей (от перемены мест слагаемых сумма в правой части формулы (2.2.3) не изменится). Пусть далее существует такая непрерывная плотность распределения p(t), которая удовлетворяет условию

,(2.2.7)

причём, при некоторых значениях t на каждом интервале k -1< t < k (k = I, 2,…, n) выполняется равенство p(t) = p_k.

На основании условия (2.2.7) величину 1-(1- p_k)^Х, входящую в формулу (2.2.3), можно аппроксимировать величиной 1-[1- p(t)]^Х. Тогда сумму в правой части формулы (2.2.3) приближённо можно заменить интегралом

. (2.2.8)

Если число разных событий n велико и вероятности отдельных событий малы, то при этих условиях будут малы также значения плотности распределения p(t). Вводя непрерывные величины х, у, на основании (2.2.8) можем записать

(2.2.9)

где у – среднее число разных событий, наступающих при х испытаниях. При этом 0 < x < ∞, 0 < y < n. Зависимость (2.2.9) является непрерывным аналогом зависимости (2.2.3).

Таким же путём из формул (2.2.9), (2.2.4) – (2.2.6') получим

(2.2.10)

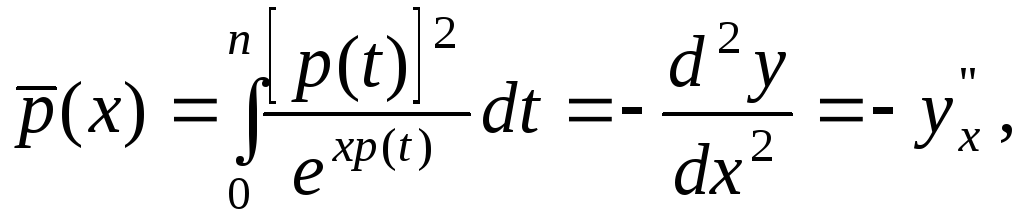(2.2.11)

(2.2.12)

Как видно из формул (2.2.10), (2.2.11), вероятность появления нового события при х произведенных испытаниях равна значению первой производной в точке (х; у) кривой роста новых событий y = f(x) (2.2.9), а средняя плотность -второй производной, взятой со знаком "минус".

Обозначим далее через средние значения вероятностей новых событий, которые могут наступитьj-ми от начала испытаний (j – порядковый номер нового события), а через – среднюю плотность распределения вероятностей новых событий, аппроксимирующую вероятности.

Поскольку переменные х и у связаны между собой функциональной зависимостью y = f(x) и, следовательно, каждому значению х соответствует определённое значение у, то справедливо равенство

где – накопленная средняя вероятностьу разных событий, наступающих при х испытаниях, или, другими словами, вероятность непоявления нового события в точке с координатами (х; у) кривой y=f(x). Принимая во внимание последнее равенство, формулу (2.2.12) можно переписать в виде

(2.2.13)

откуда дифференцированием по у найдём

(2.2.14)

или с учётом (2.2.9)

.(2.2.14′)

Средние плотности связаны между собой соотношением

(2.2.15)

которое следует из (2.2.11) и (2.2.14'). Из этих же формул при следуют равенства

, т.е. максимальные значения средних плотностей ,равны математическому ожиданию плотности распределения вероятностей разных событийp(t).

Полученные выше формулы свидетельствуют о том, что закон распределения вероятностей новых событий однозначно определяется кривой их роста y=f(x). Это замечательное свойство данной кривой даёт возможность по заданной аналитической зависимости y = f(x) находить закон распределения вероятностей новых событий (при этом используются формулы (2.2.12)–(2.2.15)), а также решать обратную задачу. Если известна функция распределения то кривая роста новых событий находится по формуле

(2.2.16)

которая следует из (2.2.12). Постоянная интегрирования С определяется из условия: у = 0 при х = 0.

Если известна функция распределения то вначале решаем дифференциальное уравнение (2.2.13) относительнох

(2.2.17)

Разрешая затем полученное уравнение относительно у (если это возможно), находим искомую функцию y = f(x).

Если известны обе функции распределения, то кривая роста находится непосредственно из равенства

(2.2.18)

Исследования показывают [16, с.58], что кривая роста новых событий должна удовлетворять условиям:

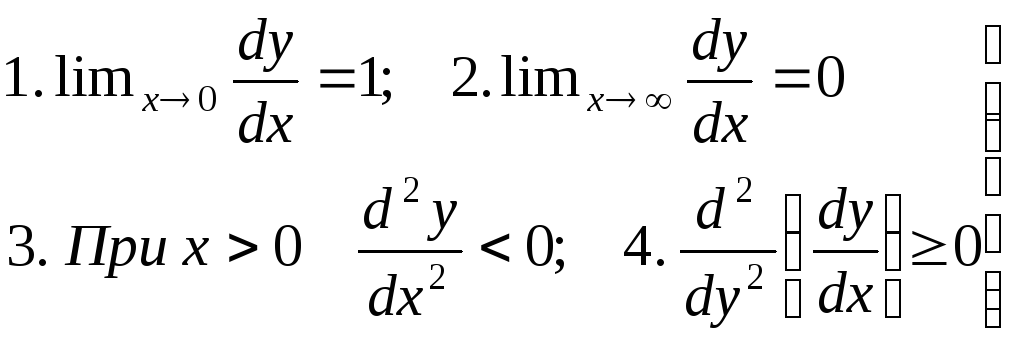(2.2.19)

Оценим степень приближения кривой y = f(x) к математическому ожиданию случайной функции М[Y(X)] при x = X. Для этого рассмотрим случай равновозможных событий, т.е. при . На основании формул (2.2.3) и (2.2.9) найдем разность:

. (2.2.20)

Расчет по формуле (2.2.20) при различных значениях n и x показывает, что разность максимальна приx = n и уменьшается с ростом n. Так, при n = 2 ; приn = 10 ; приn = 100 . Наконец, приn.

Эти результаты свидетельствуют о высокой точности аппроксимирующей кривой y = f(x).