1.8.5. Среднее квадратическое отклонение

Если извлечь из дисперсии квадратный корень, получим среднее квадратическое отклонение (обозначается σ(Х) или S(Х))

.

Размерность величины та же, что и случайной величиныХ.

Пример. По распределению

Х	2	3	10
р	0,1	0,4	0,5

требуется вычислить среднее квадратическое отклонение.

Решение.

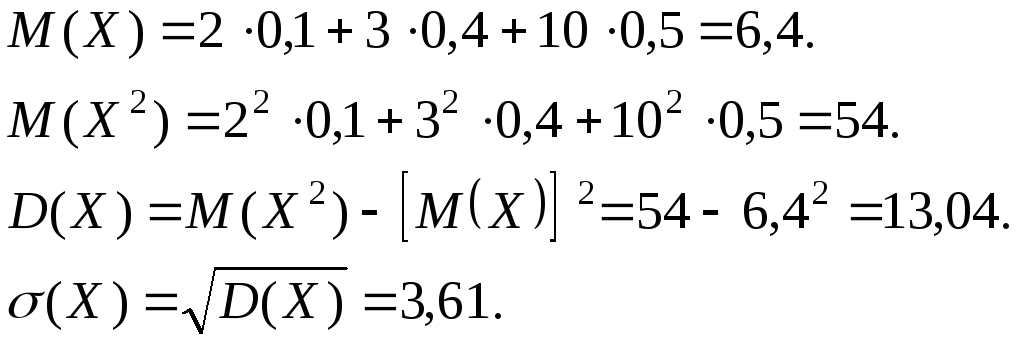
Среднее квадратическое отклонение суммы взаимно независимых случайных величин равно

.

Доказательство.

Дисперсия суммы случайных величин равна

.

Тогда

.

1.8.6. Одинаково распределенные взаимно независимые случайные величины

Рассмотрим n взаимно независимых одинаково распределенных случайных величин Х₁, Х₂,…, Х_n.

Для них среднее арифметическое равно

.

Докажем три положения [4]:

1. Математическое ожидание среднего арифметического n взаимно независимых одинаково распределенных случайных величин равно математическому ожиданию а каждой из величин

.

Доказательство:

.

2. Дисперсия среднего арифметического n взаимно независимых одинаково распределенных случайных величин в n раз меньше дисперсии D каждой из величин:

.

Доказательство:

Так как постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат, то

.

3. (следует из п.2), т.е. среднее арифметическоеn взаимно независимых одинаково распределенных случайных величин имеет значительно меньшее рассеяние (враз), чем каждая отдельная величина.

1.8.7. Моменты (начальные, центральные) дискретной случайной величины

Начальный момент порядка r – это математическое ожидание случайной величины Х^r

.

Например, начальные моменты первого и второго порядков равны

ν₁=M(X); ν ₂=M(X²).

Центральный момент порядка r задается формулой

,

при этом .

Центральный момент второго порядка представляет собой дисперсию.

Между начальными и центральными моментами существуют соотношения

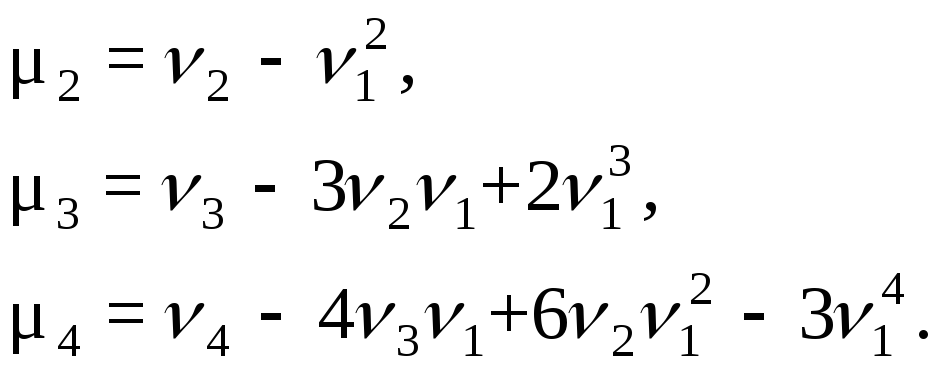
Следовательно, формула для вычисления дисперсии может быть записана в виде .

1.9. Примеры законов распределения дискретных случайных величин

1.9.1. Гипергеометрическое распределение

.

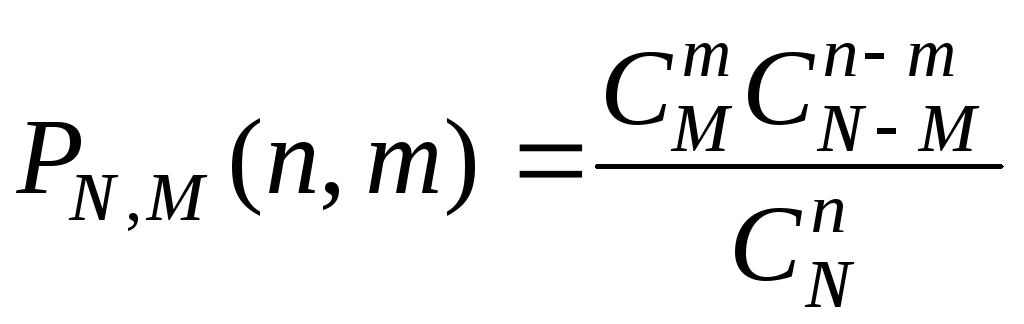В партии из N изделий М стандартных (М<N). Из партии отбирают n изделий (без возврата).

Случайная величина m – число стандартных изделий среди n отобранных имеет гипергеометрическое распределение. Оно широко используется в статистических методах контроля качества продукции.

1.9.2. Биномиальный закон

Если в гипергеометрическом распределении объем партии изделий увеличивать, то гипергеометрическое распределение будет приближаться к биномиальному закону (М/N=р)

.

Здесь выборка – с возвращением!

1.9.3. Закон Пуассона

Следует из биномиального при n→∞ и малой вероятности р (величина np – постоянная)

,

где np – среднее. При иq (или р) ≤ 0,1 закон Пуассона можно использовать вместо гипергеометрического.

1.10. Закон распределения непрерывной случайной величины

Может быть задан функцией распределения или плотностью распределения вероятностей некоторой случайной величины Х.

1.10.1. Функция распределения

Функцией распределения (интегральной функцией распределения) случайной величины Х называется функция F(х), значения которой равны вероятностям Р(Х<x)

F(x)=P(X<x)=P(–∞<X<x).

Из этого определения вытекают следующие свойства функции распределения:

0F(x)1.

F(b)F(а) при b>a, т.е. функция распределения – неубывающая.

P(aX<b)=F(b)–F(a).

, если распределение задано на всей числовой оси.

5. Если между двумя случайными величинами Х и Y существует функциональная зависимость Y=φ(X), причем, с ростом Х монотонно растет и Y, то их функции распределения равны [24]

F(x)=F(y)=F(φ(x)).

6. Если с ростом Х величина Y монотонно убывает, то

F(x)=1–F(y)=1- F(φ(x)).