4.5. Устойчивый метод

Проверка показала, что универсальный метод моментов в принципе решает задачу оценивания параметров обобщенных распределений. Однако существенным его недостатком является неустойчивость, поскольку эмпирические моменты высоких порядков () сильно зависят от значений частот на концах распределения.

Другим недостатком универсального метода моментов является то, что в системе координат на рис. 4.4.1 все типы распределений занимают только четверть площади прямоугольника. Это треугольник, ограниченный отрезком оси ординат3 < β₂ < 6 и двумя наклонными прямыми: β₂ = 6 + 0.75 β₁; β₂ = 3 + 1.5 β₁.

Доля площади прямоугольника, в котором задано распределение, может служить показателем разрешающей способности метода оценивания параметров. Чем ближе она к единице, тем выше разрешающая способность метода.

Автором обобщенных распределений был разработан устойчивый метод оценивания параметров [12, 16, 18], который по точности не уступает методу наибольшего правдоподобия, но значительно проще последнего.

Здесь так же, как и в случае универсального метода моментов, вводятся два показателя – асимметрии В и островершинности Н, которые зависят от двух параметров формы k=γ/β, u. По этим показателям устанавливается тип выравнивающей кривой распределения и находятся оценки параметров k, u. Оценки двух других параметров рассчитываются по простым формулам.

Достоинством метода является его устойчивость, т.е. он мало чувствителен к выбросам на концах статистического распределения. Кроме того, разрешающая способность метода составляет примерно 80%, что значительно выше аналогичного показателя универсального метода моментов.

К недостаткам его следует отнести то, что для оценивания параметров выравнивающей кривой он требует группирования статистических данных, так же как и метод наибольшего правдоподобия.

Если обобщенное распределение задано плотностью р(x), то показатели В, Н равны

, (4.5.1) где

. (4.5.2)

Исследования показали, что величина Н задана на интервале , а величинаВ – на интервале –1/4<B<1/4.

Вычислим для разных типов распределений значения показателей В, Н при различных значениях параметров k, u. Далее построим номограмму (приложение 3). Она применима к трем основным системам непрерывных распределений, заданным первыми плотностями. При этом они должны быть приведены к форме плотности р(х).

На номограмме распределения II, II и IV типов представлены кривыми. Типы I, I, III, V занимают определенные области. Симметричные распределения IIIc, Vc типов представлены отрезками на оси ОН: для IIIc типа ; для Vc типа. Распределения IVс типа представлены точкой. Распределения IIс типа также представлены точкой.

На номограмме изображены области распределений с левосторонней асимметрией, для которых . Сюда относится часть распределений III–V типов при 0<k<(1–1/u)/2, а также распределения I, II типов. При этом распределения приведены к форме плотности р(х).

Распределения I, II типов, а также часть распределений III-V типов при (1–1/u)/2<k<1–1/u имеют правостороннюю асимметрию. Для них –1/4<B<0, причем для распределений I, II и I, II типов справедливы равенства: .

Здесь следует отметить, что для распределений с параметром сдвига l и параметром β = 1 автором построена другая номограмма, которая является продолжением настоящей. В книге она не приведена, но без ее использования невозможно разработать программу для установления типа указанных распределений и вычисления оценок параметров k, u.

Таким образом, показатели В, Н однозначно определяют тип распределения, приведенного к форме плотности р(х). Более того, с помощью этих показателей могут быть найдены оценки параметров k, u непосредственно из номограммы.

Для распределений III–V типов при В < 0 из номограммы вначале находятся оценки параметров k, u (при В > 0), затем вычисляется величина k=1–1/u–k.

Оценка параметра β для всех типов равна [16]

. (4.5.3)

Тогда γ = kβ.

Оценки параметра  для распределений II, II типов и произведения αu для остальных типов равны [12, 16]:

, (4.5.4) где в зависимости от типа распределения величины ирассчитываются по формулам:

Типы I, I:

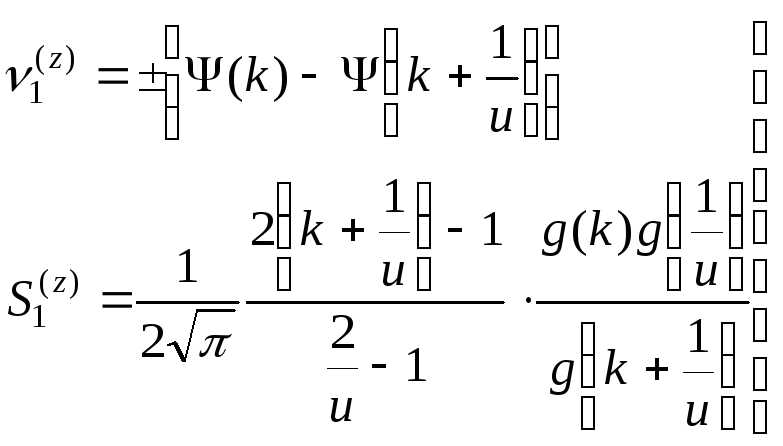; (4.5.5)

Типы II, II:

; (4.5.6)

Типы III-V:

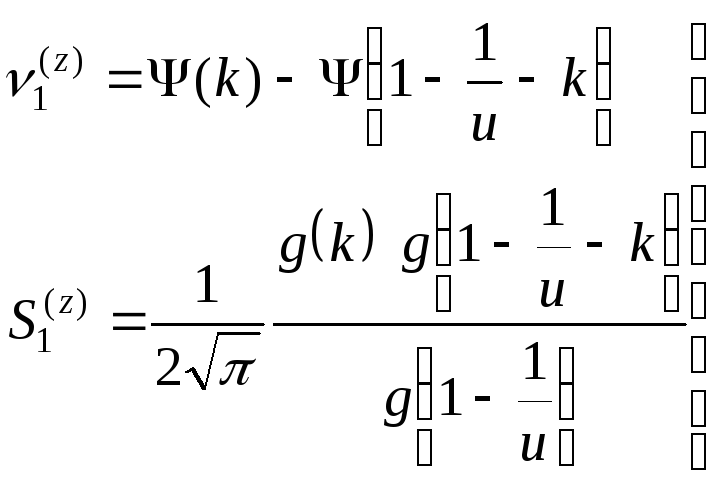. (4.5.7)

Величина

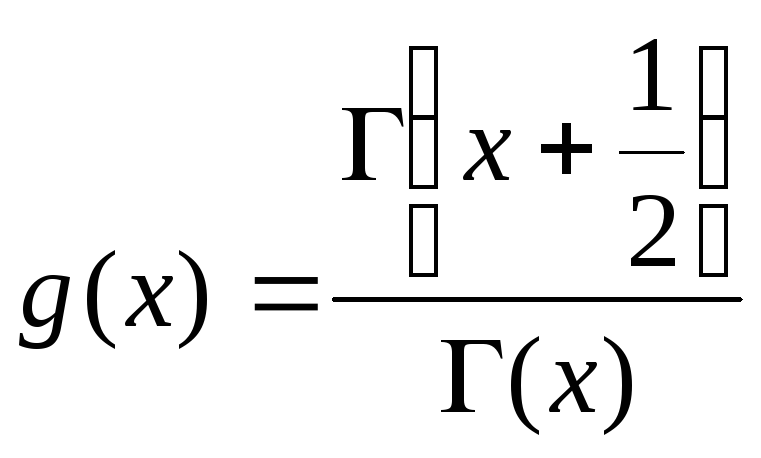(4.5.8) может быть вычислена по приближенным формулам:

– при x ≥ 4

(4.5.9)

– при 0<x<4

, (4.5.10) где

(4.5.11)

Для облегчения расчетов в приложении 1 приводятся также значения функции g(x). Величина Ψ(x) вычисляется по первой из формул (4.4.14).

Для установления типа выравнивающей кривой распределения и нахождения оценок параметров по устойчивому методу достаточно найти значения статистических показателей и приравнять их соответствующим теоретическим.Эти показатели для каждой системы непрерывных распределений вычисляются по-своему. Но номограмма применима ко всем трем системам непрерывных распределений.

Оценки статистических показателей в случае выравнивающих распределений, заданных плотностью р(х), вычисляются по формулам:

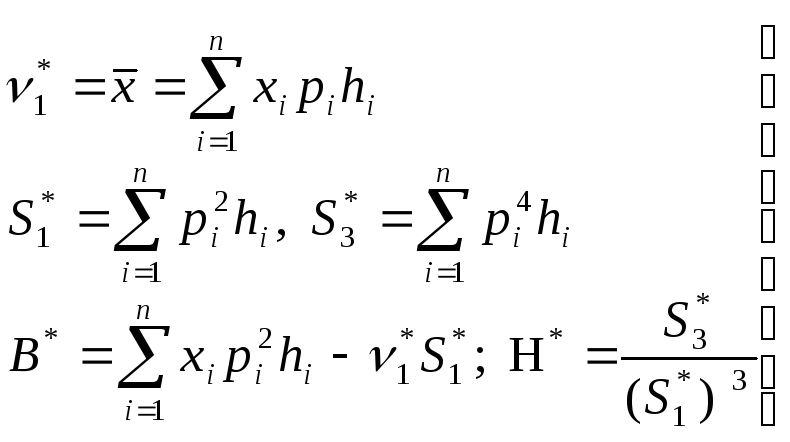, (4.5.12)

где р_i=m_i/(Mh_i) – эмпирическая плотность распределения; m_i – наблюденная частота случайной величины Х в i-ом интервале – наблюденная частота во всехn интервалах (объем выборки); h_i – ширина i-го интервала; х_i – значение случайной величины Х в середине i-го интервала.

Формулы (4.5.12) можно выразить через абсолютные частоты m_i:

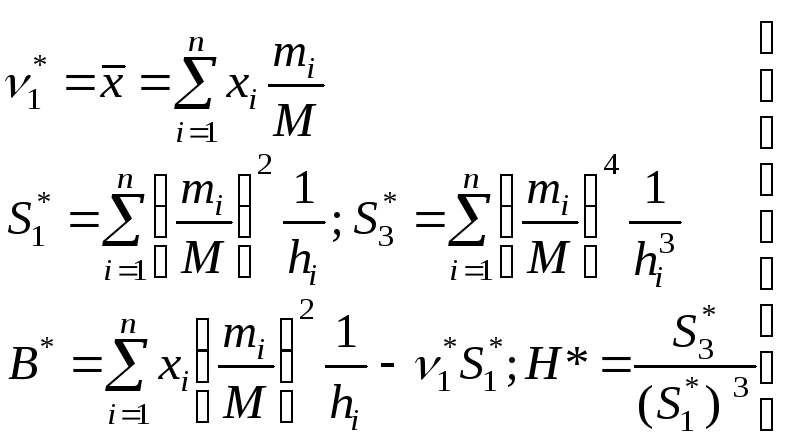. (4.5.13)

Показатель островершинности Н* при h_i = const примет вид

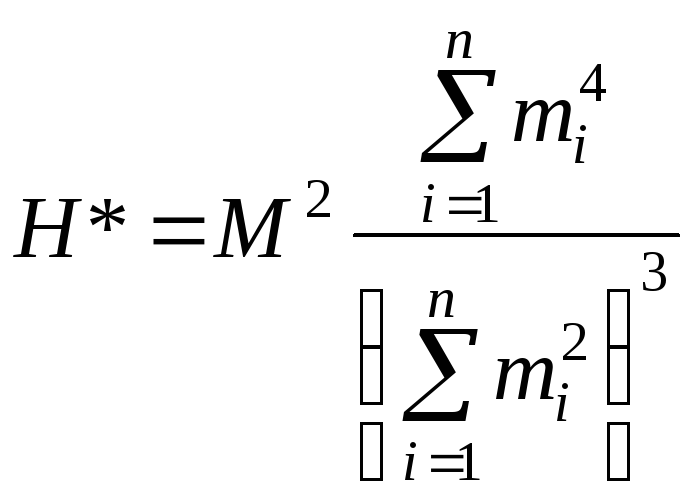, (4.5.14) т.е. ширина интервала не входит в формулу (4.5.14). Отсюда следует вывод, что ширину интервала группирования статистических данных лучше принимать постоянной (по крайней мере для распределений, близких к симметричным).

Если выравнивающее распределение задано обобщенной плотностью p(t), статистические показатели рассчитываются по формулам:

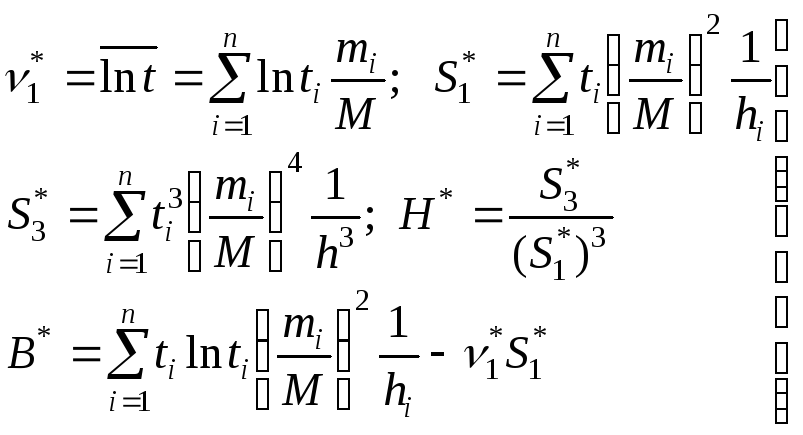. (4.5.15)

При h_i = const

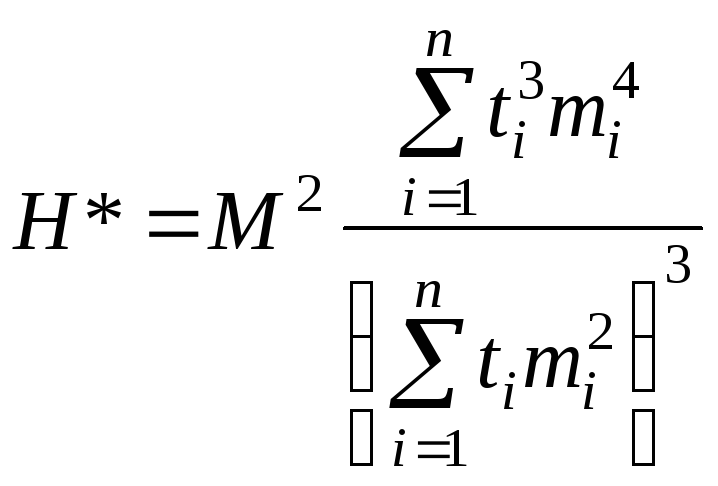. (4.5.16)

Если выравнивающее распределение задано плотностью p(y), то статистические показатели вычисляются по формулам:

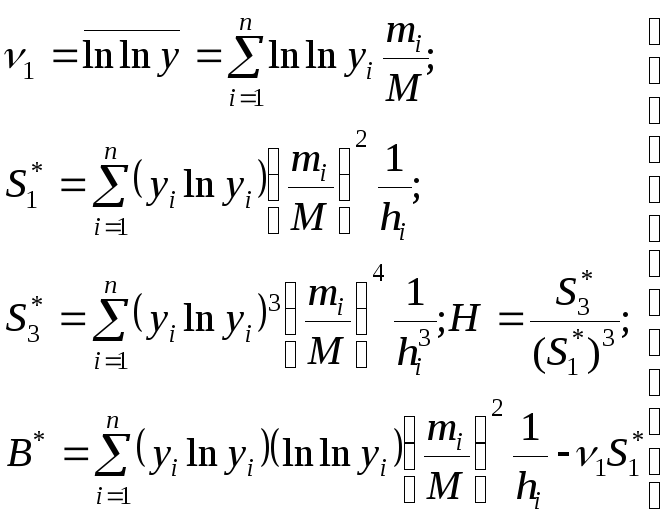. (4.5.17)

Поскольку метод применим к трем системам непрерывных распределений, то его можно считать общим устойчивым методом.

Для установления типа выравнивающей кривой и нахождения оценок параметров по общему устойчивому методу автором созданы программы .

В заключение отметим, что устойчивый метод основан на взаимосвязи между законами распределения случайных величин Х и Z. Запишем обобщенную плотность р(х)

.

Пусть для определенности параметр u > 0.

Введем случайную величину

. (4.5.18)

Тогда плотность р(z) будет равна

.

Поскольку на основании (4.5.17) , то

, (4.5.19)

откуда имеем замечательное равенство

βzp(z)=p(x). (4.5.20)

На его базе строится устойчивый метод оценивания параметров.

Поскольку плотность р(z) является функцией двух параметров формы , то последняя формула позволяет ввести критерии, зависящие от этих двух параметров.

Запишем на основании формулы (4.5.20) следующее равенство:

.

Введем обозначения

.

Тогда последнее равенство перепишется в виде

. (4.5.21)

Формула (4.5.21) позволяет найти значение параметра β (например, при r =1), а также получить критерий островершинности, зависящий от двух параметров k, u. Для этого необходимо взять отношение либо. Последнее оказалось наиболее подходящим.

Таким путем был получен показатель островершинности Н.

Показатель асимметрии В найден из условия, чтобы для симметричных распределений он был равен нулю и в то же время использовал ранее введенные величины. Такой показатель может иметь вид

или

.

Покажем, что он зависит от двух параметров k, u.

Поскольку , то

.

По показателям В, Н строится номограмма, позволяющая устанавливать тип выравнивающей кривой распределения и находить оценки параметров k, u. Оценка параметра β вычисляется по величинам . Оценка параметра α или произведения αu вычисляется по тем же формулам, что и в случае универсального метода моментов.

Если в качестве показателей асимметрии и островершинности использовать величины

где x_с – мода, то можно построить аналогичную номограмму для установления типа выравнивающей кривой распределения и нахождения в первом приближении оценок параметров k, u по координатам одной характерной точки С и среднему значению плотности р(х).