2.3. Установление статистической структуры выборки по кривой роста новых событий

По заданной кривой роста новых событий можно рассчитать количество событий, наступающих ровно 0, 1…, m раз при х испытаниях, т.е. установить статистическую структуру выборки (частотный спектр). Решим эту задачу в общем виде.

Найдём вероятность того, что k-ое событие при Х испытаниях появится ровно m раз. Как известно, эта вероятность определяется по формуле Бернулли

(2.3.1)

В случае полной группы несовместных событий вероятность P_k(m,Х) совпадает с математическим ожиданием числа появлений отдельного k-го события ровно m раз при Х испытаниях. Поэтому математическое ожидание числа всех тех разных событий, которые появятся ровно m раз при Х испытаниях, будет равна сумме

(2.3.2)

Формула (2.3.2) позволяет установить статистическую структуру выборки по известному закону распределения вероятностей разных событий, составляющих полную группу.

Если вероятности отдельных событий малы, а число испытаний X достаточно большое, то вероятности р_k целесообразно аппроксимировать непрерывной плотностью p(t), удовлетворя­ющей условию (2.2.7), а формулу (2.3.2) представить в виде

(2.3.3)

Формулу (2.3.3) при х → ∞ и ограниченных значениях m можно несколько упростить. Действительно

,

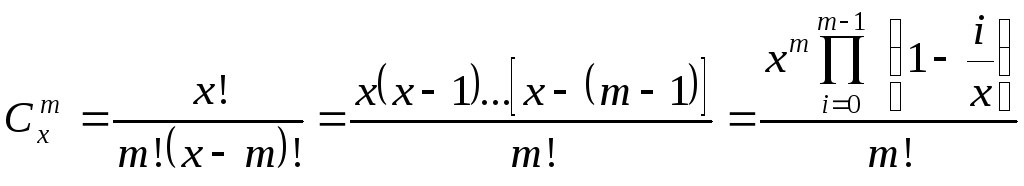что при х → ∞ дает

(2.3.4)

В то же время при х → ∞

Формула (2.3.3) с учетом (2.3.4) и последнего равенства примет вид

(2.3.5)

где – среднее значение количества разных событий, насту­пающих ровноm раз при х испытаниях. При этом должны выполняться равенства

(2.3.6)

С другой стороны, дифференцируя выражение (2.2.9) m раз по х, найдем

(2.3.7)

Подставляя в (2.3.5) вместо определенного интеграла его значение из (2.3.7), получим окончательно

(2.3.8)

Формулы (2.3.8) и (2.3.16) дают возможность связать частотный спектр со средней плотностью [27, с.21]

(2.3.9)

Итак, для установления статистической структуры выборки достаточно знать либо кривую роста новых событий, либо среднюю плотность распределения вероятностей новых событий – В первом случае используется формула (2.3.8), во втором – (2.3.9).

2.4. Восстановление кривой роста новых событий по статистической структуре выборки

Перепишем формулу (2.3.8) в виде

(2.4.1)

Зависимость (2.4.1) была установлена В.М.Калининым [6, с. 247]. Из (2.4.1) следует, что функция у = f(x) бесконечно дифференцируема. Это позволяет строить ее разложение в ряд Тейлора. В.М.Калинин получает таким способом формулу для кривой роста новых событий, которая в наших обозначениях имеет вид [6, c. 247]

(2.4.2)

Здесь – число разных событий в выборке объемом– числоm – разовых событий в выборке ;y – ожидаемое среднее число разных событий в подвыборке произвольного объема х (x<x₀).

Формула В.М. Калинина (2.4.2) позволяет восстановить кривую роста новых событий по заданной статистической структуре выборки

Подставляя в (2.4.2) опытные значения величин , нетрудно рассчитать значенияy при заданных x. Практически формулой (2.4.2) удобно пользоваться при 0,1.

При < 0,05 целесообразно воспользоваться формулой (2.2.3).

Предположим, что разные события, которые встретились в выборке объемом , упорядочены по невозрастанию эмпирических частот, гдеr – порядковый номер (ранг) события (r = 1, 2,…,). Учитывая далее, что оценкой вероятности является относительная частота(по крайней мере при достаточно больших значениях), на основании формулы (2.2.3) можем записать

(2.4.3)

При малых значениях отношения из ( 2.4.3) имеем

(2.4.4)

Так как события упорядочены по невозрастанию частот, то сумму (2.4.4) приближенно можно вычислить по формуле прямоугольников. Это значительно сокращает объем вычислительных работ.