1.10.2. Плотность распределения

Плотностью распределения (дифференциальным законом распределения) непрерывной случайной величины Х называется первая производная от функции распределения

.

График плотности распределения называется кривой распределения.

Свойства плотности распределения.

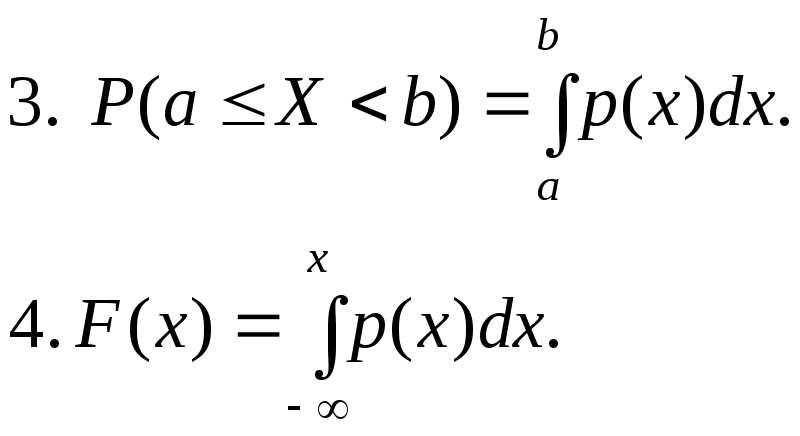
Если между двумя случайными величинами Х и Y существует функциональная зависимость Y=φ(Х), то взаимосвязь между плотностями распределения р(х) и р(у) задается формулой

Действительно, пусть с ростом Х растет Y. Тогда F(x)=F(y)=F(φ(x)) (см. свойства функции распределения). По правилу дифференцирования сложной функции находим

или, поскольку y = φ(x),

В случае, если с ростом Х величина Y убывает, первая производная dy/dx < 0, но плотность p(x) > 0. Поэтому в общем случае первая производная берется по абсолютной величине.

Рассмотрим примеры.

Пример 1. Из равенства функций распределения F(x) = F(lnx) требуется найти соотношение между плотностями p(x) и p(lnx).

Дифференцируя последнее равенство по x, имеем:

откуда xp(x) = p(lnx).

Пример 2. Задана плотность распределения (показательный закон)

.

Найти: N – нормирующий множитель; F(x) – функцию распределения; вероятность попадания случайной величины Х на интервал 3<x<5.

Используем свойства плотности:

.

Отсюда N = , т.е.

.

Далее функция распределения равна

.

Вероятность попадания случайной величины Х на заданный интервал равна

.

Пусть далее некоторая случайная величина Y связана со случайной величиной Х зависимостью Y=1/X.

Найдем функцию распределения F(y) и плотность р(у).

Так как здесь с ростом Х величина Y убывает, то

.

Но Х=1/Y, поэтому

.

Отсюда плотность р(у) равна

.

Плотность р(у) можно найти непосредственно по плотности р(х).

Поскольку Х=1/Y, dх/dy=–1/y², то

.

Пример 3. Случайная величина Х распределена по показательному закону с плотностью и функцией распределения

.

Рассмотрим случайную величину Y = lnX и найдем ее закон распределения. Имеем

Но в последних двух формулах величина y = lnx. Следовательно, их можно представить в виде

т.е. доказана справедливость равенств

Аналогично доказываются другие равенства, например, приx>0 и

при x > – . Они следуют непосредственно из определения функции распределения и свойств случайных величин. Покажем это на следующем примере.

Пример 4. На испытания поставлено 100 механизмов. Пусть за время t < 12 месяцев отказало 8 из них, т.е. доля отказавших механизмов равна 8/100 = 0.08. Эта величина является оценкой вероятности P(T < 12), или оценкой функции распределения

F(t) = P(T < t) = 0.08.

Если время наработки до отказа выразить в других единицах (сутках, неделях), то для нашего примера будет справедливо равенство

F(t) = F(ct),

поскольку доля отказавших механизмов за один и тот же период времени (12 месяцев, или 365 суток) одна и та же.

Дифференцируя последнее равенство по t, найдем соотношение между плотностями p(ct) и p(t)

Из последней формулы следует, что при увеличении случайной величины Т в С раз новая плотность p(ct) получается из предыдущей путем уменьшения плотности p(t) в С раз.

Итак, если имеется группированный вариационный ряд распределения случайной величины Т, то для построения нового ряда распределения случайной величины СТ достаточно увеличить в С раз границы интервалов, не изменяя их частот. При этом эмпирическая плотность будет вС раз меньше соответствующей плотности за счет увеличения ширины интервалов вС раз.