
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. АНАЛИЗ И РАСЧЁТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
- •1.1. Электрическая цепь и её элементы
- •1.2. Основные электрические величины цепи постоянного тока
- •1.3. Резистивный элемент
- •1.4. Схемы замещения источников электрической энергии
- •1.5. Основные законы цепей постоянного тока
- •1.6. Потенциальная диаграмма электрической цепи
- •1.7. Эквивалентные преобразования в резистивных цепях
- •1.8. Методы расчёта цепей постоянного тока
- •1.8.2. Метод контурных токов
- •1.8.3. Метод узловых потенциалов
- •1.8.5. Метод эквивалентного генератора
- •1.9. Баланс мощностей
- •1.10. Расчёт нелинейных цепей постоянного тока
- •Контрольные вопросы и задания
- •2.1. Основные понятия переменного тока
- •2.2. Способы представления синусоидальных величин
- •2.3. Элементы электрической цепи синусоидального тока
- •2.3.1. Индуктивный элемент
- •2.3.2. Ёмкостный элемент
- •2.5. Законы Кирхгофа для цепей синусоидального тока
- •2.9. Мощности в цепях синусоидального тока
- •2.10. Учёт взаимно индуктивных связей при анализе электрических цепей
- •Контрольные вопросы и задания
- •3.1. Общие сведения
- •3.2. Схема соединения звездой в трёхфазных цепях
- •3.3. Схема соединения треугольником в трёхфазных цепях
- •3.5. Мощность в трёхфазных цепях
- •3.6. Измерение мощности трёхфазной цепи
- •Контрольные вопросы и задания
- •4.3. Расчёт цепей несинусоидального периодического тока
- •Контрольные вопросы и задания
- •5.1. Элементы магнитной цепи
- •5.2. Основные величины и законы магнитных цепей
- •5.3. Свойства и характеристики ферромагнитных материалов
- •5.4. Расчёт неразветвленной магнитной цепи
- •5.5. Электромеханическое действие магнитного поля
- •5.7. Мощность потерь в магнитопроводе
- •Контрольные вопросы и задания
- •6.1. Общие сведения
- •6.2. Устройство однофазного трансформатора
- •6.3. Принцип действия однофазного трансформатора
- •6.4. Схема замещения однофазного трансформатора
- •6.5. Работа трансформатора в режиме холостого хода
- •6.6. Работа трансформатора в режиме короткого замыкания
- •6.8. Мощности трансформатора
- •6.11. Автотрансформаторы
- •Контрольные вопросы и задания
- •7.1. Общие сведения
- •7.3. Режимы работы трёхфазных асинхронных машин
- •7.4. Принцип действия трёхфазных асинхронных двигателей
- •7.5. Мощность и КПД трёхфазных асинхронных двигателей
- •7.6. Механические характеристики асинхронных двигателей
- •7.7. Пуск трёхфазных асинхронных двигателей
- •7.9. Однофазные асинхронные двигатели
- •Контрольные вопросы и задания
- •8.1. Общие сведения
- •8.2. Устройство трёхфазных синхронных машин
- •8.3. Разновидности трёхфазных синхронных машин
- •8.5. Принцип действия трёхфазных синхронных машин
- •8.6. Работа синхронного генератора в режиме холостого хода
- •8.7. Работа синхронного генератора в режиме короткого замыкания
- •8.8. Работа синхронного генератора в режиме нагрузки
- •8.9. Мощность и КПД трёхфазных синхронных машин
- •8.10. Характеристики трёхфазных синхронных машин
- •8.11. Пуск трёхфазных синхронных двигателей
- •Контрольные вопросы и задания
- •9.1. Общие сведения
- •9.2. Принцип действия коллектора
- •9.3. Устройство машин постоянного тока
- •9.5. Реакция якоря
- •9.6. Мощность и КПД машин постоянного тока
- •9.8. Характеристики генераторов постоянного тока
- •9.9. Характеристики двигателей постоянного тока
- •9.11. Регулирование частоты вращения двигателей постоянного тока
- •Контрольные вопросы и задания
- •10.ОСНОВЫ ЭЛЕКТРОНИКИ
- •10.1. Общие сведения о полупроводниках
- •10.2. Полупроводниковые устройства
- •10.2.2. Биполярные транзисторы
- •10.2.3. Полевые транзисторы
- •10.2.4. Тиристоры
- •10.2.5. Классификация электронных устройств
- •Контрольные вопросы и задания
- •10.3. Источники вторичного электропитания
- •10.3.1. Полупроводниковые выпрямители
- •10.3.2. Управляемые выпрямители
- •10.3.3. Регуляторы переменного тока
- •10.3.4. Инверторы
- •Контрольные вопросы и задания
- •10.4. Усилители электрических сигналов
- •10.4.1. Классификация усилителей
- •10.4.3. Операционные усилители
- •Контрольные вопросы и задания
- •10.5. Генераторы синусоидальных колебаний
- •Контрольные вопросы и задания
- •10.6. Импульсные и цифровые электронные устройства
- •10.6.1. Работа операционного усилителя в импульсном режиме
- •10.6.2. Логические элементы
- •10.6.4. Импульсные устройства с устойчивым состоянием. Триггеры
- •Контрольные вопросы и задания
- •10.7. Программируемые устройства. Микропроцессоры
- •Контрольные вопросы и задания
- •11.1. Методы измерений
- •11.2. Средства измерений
- •11.3. Погрешности измерений
- •Контрольные вопросы и задания
- •ЗАКЛЮЧЕНИЕ
- •Библиографический список
- •ОГЛАВЛЕНИЕ

На рис. 2.15, б показаны частотные характеристики параллельного контура. В ёмкостном элементе ток IC = ωCU возрастает про-
порционально угловой частоте, в индуктивном элементе ток IL =U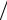 (ωL) обратно пропорционален угловой частоте, в резистивном
(ωL) обратно пропорционален угловой частоте, в резистивном
элементе IG = GU от угловой частоты не зависит. Точка пересечения кривых IC(ω) и IL(ω) соответствует резонансу токов.
Ток в цепи при резонансе достигает минимального значения, т.к.
реактивные провод мости компенсируют друг друга: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
=U |
|
|
|
|
|
|
|
|
G2 +(B |
|
|
)2 |
|
|
||
I |
р |
=UY |
=U |
|
Lр |
− B |
G2 +02 |
=UG . |
(2.90) |
|||
|
|
|
|
|
Cр |
|
|
|
|
|
||
С |
резонансе токов общий ток параллельного RLC |
|||||||||||
Поэтому |
||||||||||||
участка равен току рез |
стивного элемента: |
|
|
|||||||||
при I = IG. |
|
|
|
L может |
(2.91) |
|||||||
Последовательно |
|
с индуктивным элементом |
быть |
|||||||||
включен рез ст вный элемент RL, а последовательно с ёмкостным |
||||||
элементом C – рез ст вный элемент RC, учитывающие, например, по- |
||||||
А |
|
|||||
тери мощности в проводах. Условием резонанса токов в такой цепи |
||||||
будет равенствобиндуктивной и ёмкостной проводимостей этих вет- |
||||||
вей в соответствии с формулой (2.89). |
|
|
|
|||
|
X L |
= |
|
X C |
. |
(2.92) |
|
|
|
||||
R2 |
+ X 2 |
Д |
|
|||
|
R2 |
+ X 2 |
|
|||
L |
L |
|
C |
C |
|
|
И в этом случае при резонансе общий ток совпадает по фазе с напряжением.
безопасное для энергетических установок и широко применяется в радиотехнических устройствах.
Резонанс токов в отличие от резонанса напряжений – явление И
2.9. Мощности в цепях синусоидального тока
Пассивный двухполюсник можно представить эквивалентной схемой замещения в виде последовательного соединения двух элементов: с активным сопротивлением R и реактивным сопротивлением X. Определим мгновенную мощность пассивного двухполюсника, равную мгновенной мощности источника ЭДС при напряжении и токе [6]:
u =U m sin(ωt +ψu ); i = Im sin(ωt +ψi ).
63
Мгновенная мощность |
|
||||
|
p = ui =Um Im sin(ωt + ψu )sin(ωt + ψi )= |
|
|||
|
= |
Um Im |
[cos(ψu −ψi )+cos(2ωt +ψu +ψi )]. |
(2.93) |
|
|
|
||||
|
2 |
|
|
|
|
С |
|
|
|||
Энергетический процесс складывается из уже рассмотренных |
|||||
энергетических процессов для идеальных элементов. Часть электри- |
|||||
ческой энерг |
|
сточн |
ка поступает в двухполюсник и преобразуется |
||
в друг е в ды энерг |
. Другой частью энергии источник и двухпо- |
||||
или |
|
||||
люсник пер од чески обмениваются. |
|
||||
Из выражен я (2.93) следует, что средняя мощность пассивного |
|||||
двухполюсн ка за пер од |
|
||||
|
|
|
|
T |
|
|
|
P |
= 1 ∫ pdt =UI cos(ψu −ψi ), |
|
|
б |
|
||||
|
|
|
|
T 0 |
|
|
|
|
|
P =UI cos ϕ. |
(2.94) |
Выражен е (2.94) определяет активную мощность двухполюс-
ника и сточн ка, которая зависит от действующих значений напря-
жения и тока, а также cosφ – коэффициента мощности [6]. Активная |
|||||
мощность всегда положительна и не зависит от знака угла φ, она о п- |
|||||
ределяет энергетический режим пассивного двухполюсника в целом, |
|||||
т.е. среднюю скорость нео ратимого преобразования энергии во всех |
|||||
резистивных элементах пассивного двухполюсника. |
|
||||
Из треугольниковАнапряжений и сопротивлений (см. рис. 2.10, б, в) |
|||||
пассивного двухполюсника следует, что коэффициент мощности |
|||||
cosϕ = R |
= |
UR |
. |
|
(2.95) |
|
|
||||
Z |
|
U |
|
|
|
Д |
|
||||
После замены cosφ в уравнении (2.94) получим другие выраже- |
|||||
ния для активной мощности пассивного двухполюсника: |
|
||||
P =UR I = RI 2 . |
|
(2.96) |
|||
|
|
|
|
И |
|
Произведение действующих значений напряжения между выводами источника U = E и тока источника I в выражении (2.94) определяет полную мощность источника, равную полной мощности пассив-
ного двухполюсника: |
|
S =UI = EI = ZI 2 . |
(2.97) |
64
|
Размерности активной и полной мощности совпадают, но для из- |
||||||||||||
мерения полной мощности выбрана своя единица – вольт-ампер [ВА]. |
|||||||||||||
|
Полная мощность определяет эксплуатационные возможности |
||||||||||||
многих электротехнических устройств (генераторов, трансформато- |
|||||||||||||
ров, электрических машин и др.) Для большинства потребителей ко- |
|||||||||||||
эффициент мощности cosφ = P/S < 1, поэтому энергетические воз- |
|||||||||||||
можности источника используются не полностью (P < S). |
|
||||||||||||
|
Для анализа энергетических процессов в цепи при неполном ис- |
||||||||||||
пользован |
|
энергет |
ческих возможностей источника вводится поня- |
||||||||||
тие реакт вной мощности источника, равной реактивной мощности |
|||||||||||||
пассивного двухполюсника: |
|
|
|
|
|
|
|||||||
С |
|
|
Q =UI sin ϕ. |
|
|
(2.98) |
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
Из |
треугольн ка |
сопротивлений |
пассивного двухполюсника |
|||||||||
(см. |
. 2.10, в) следует, что sin ϕ = X Z , поэтому |
|
|||||||||||
рис Q = XI 2 . |
|
|
(2.99) |
||||||||||
|
Реакт вная мощность пассивного двухполюсника может быть |
||||||||||||
положительной и отрицательной в зависимости от знака угла φ. |
|||||||||||||
|
Связьбактивной, реактивной и полной мощностей пассивного |
||||||||||||
двухполюсника удо но интерпретировать геометрически на ком- |
|||||||||||||
плексной плоскости (рис. 2.16). Для этого необходимо умножить все |
|||||||||||||
стороны треугольника сопротивлений на I2. Вновь полученный тре- |
|||||||||||||
угольник называется треугольником мощностей. |
|
||||||||||||
|
|
|
|
|
А |
|
|||||||
|
∙ |
+j |
|
|
|
а |
|
|
|
∙ |
+j |
P=RI2 |
б |
|
I |
|
|
|
|
|
|
|
|
I |
0 |
|
+1 |
|
|
|
|
S=ZI2 |
|
|
|
|
|
|
φ |
||
|
|
|
|
|
|
|
|
|
|
|
–jQ = –jXI2 |
||
|
R |
|
|
|
|
|
|
|
R |
|
|
||
U∙ |
|
|
|
|
|
|
|
2 |
Д2 |
||||
jX |
|
|
φ |
|
|
jQ=jXI |
|
U∙ |
jX |
|
S=ZI |
|
|
|
|
|
0 |
P=RI |
2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
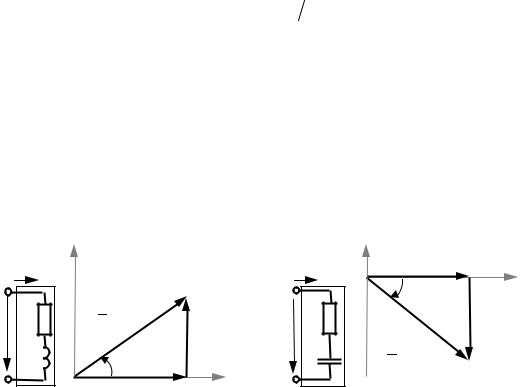
Рис. 2.16. Треугольники мощностей для смешанного характера нагрузки: |
|||||||||||||
|
а – активно-индуктивный характер; б – активноИ-ёмкостный характер |
||||||||||||
|
Комплексная мощность в цепи синусоидального тока определя- |
||||||||||||
ется по формуле |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
* |
|
|
|
|
|
|
|
|
(2.100) |
|
|
|
|
S =U I =UI cos ϕ+ jUI sin ϕ = P + jQ = Se jϕ , |
|||||||||
* |
– сопряжённый комплекс тока. |
|
|
|
|
||||||||
где I |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
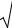
Полная мощность |
|
|
|
|
S = |
|
|
. |
|
P2 +(Q2 |
−Q2 ) |
(2.101) |
||
|
L |
C |
|
|
В любой момент времени алгебраическая сумма мгновенных мощностей всех источников энергии равна алгебраической сумме мгновенных мощностей всех приёмников энергии.
Баланс мощности в электрической цепи синусоидального тока, содержащей произвольное число источников энергии и потребителей энергии, означает, что, во-первых, алгебраическая сумма активных
мощностей всех |
сточн ков энергии равна сумме мощностей всех ре- |
|||||||||
ников |
|
|
|
|
||||||
зистивных элементов: |
|
|
|
|
|
|||||
С∑U стIист cos(ψu −ψi )= ∑RIR2 , |
(2.102) |
|||||||||
во-вторых, алгебра ческая сумма реактивных мощностей всех источ- |
||||||||||
|
б |
|
|
|
|
|||||
энерг |
равна разности между арифметической суммой реак- |
|||||||||
тивных мощностей |
ндуктивных элементов и арифметической сум- |
|||||||||
мой реакт вных мощностей ёмкостных элементов: |
|
|||||||||
|
|
|
∑U стI ст sin(ψu −ψi )= ∑ X L IL2 −∑ X C IC2 . |
(2.103) |
||||||
Баланс мощностей можно представить в комплексной форме |
||||||||||
|
|
|
|
m |
* |
n |
− X Ck )], |
|
||
|
|
|
∑ |
E p I p = ∑[Ik2 Rk + jIk2 (X Lk |
(2.104) |
|||||
|
|
|
p=1 |
|
k =1 |
|
|
|
|
|
m |
|
* |
|
– алгебраическая мощность всех источников ЭДС; |
||||||
здесь ∑E |
|
I p =S |
||||||||
p=1 |
p |
|
|
|
А |
|
||||
положительны те из слагаемых, для которых направление действия |
||||||||||
ЭДС Ėр и соответствующего тока İр через Э |
|
С совпадают, в против- |
||||||||
ном случае |
|
слагаемое |
n |
|
|
= P – алгебраическая |
||||
|
отрицательно; ∑I 2 R |
k |
||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
Дk=1 |
||||
сумма мощностей на активных сопротивлениях (здесь должны быть |
||||||||||
учтены как внешние сопротивления, так и сопротивления самих ис- |
||||||||||
точников энергии); |
n |
n |
– алгебраическая сумма |
|||||||
∑Ik2 X Lk − ∑Ik2 X Ck = Q |
||||||||||
|
|
|
|
|
k=1 |
k=1 |
И |
|||
мощностей на реактивных сопротивлениях. |
||||||||||
Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению коэффициента мощности cosφ в силовых электрических цепях.
66
Следует указать, что подавляющее большинство потребителей |
|||||||||||||
(электродвигатели, электрические печи, другие различные устройства |
|||||||||||||
и приборы) как нагрузка носит активно-индуктивный характер. Чтобы |
|||||||||||||
увеличить значение cosφ и разгрузить электротехническое оборудо- |
|||||||||||||
вание от реактивного (индуктивного) тока, необходимо включить па- |
|||||||||||||
раллельно электротехническому устройству батарею конденсаторов. |
|||||||||||||
Реактивный (ёмкостный) ток батареи конденсаторов компенсирует |
|||||||||||||
реактивный (индуктивный) ток приёмника. |
|
|
|
||||||||||
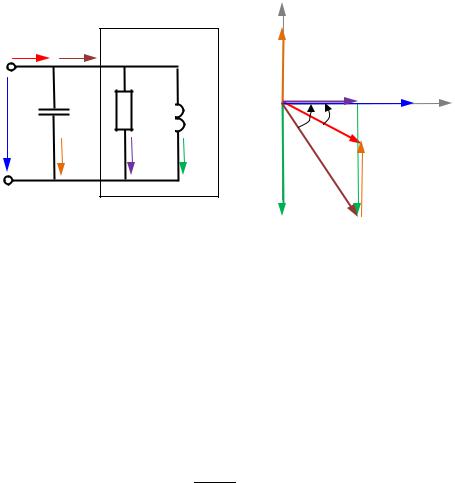
Представ м пр ёмник в виде эквивалентной схемы замещения |
|||||||||||||
пассивного двухполюсника (рис. 2.17, а). Компенсация индуктивного |
|||||||||||||
тока нагрузки ILн |
при помощи батареи конденсаторов показана на век- |
||||||||||||
Сторной д аграмме (р с. 2.17, |
б), из которой видно, что коэффициент |
||||||||||||
|
|
после |
включения |
атареи |
конденсаторов |
увеличивается: |
|||||||
cosφ > cosφн. В |
ольш нстве случаев допустима неполная компенса- |
||||||||||||
ция сдв га фаз. Наличие |
|
не ольшого индуктивного тока при |
|||||||||||
cos ϕ ≥ 0,95 |
не создаёт дополнительных потерь. |
|
|
||||||||||
мощности |
|
|
|
|
|
|
|
||||||
а ∙ |
|
∙ |
П |
итель |
|
|
+j |
∙ |
б |
|
|
||
I |
|
Iн |
|
|
|
|
|
|
|
||||
|
отребIC |
I∙Rн |
|
|
|||||||||
–jXC |
|
jXL |
|
|
|
|
0 |
|
φ |
|
+1 |
||
U∙ |
|
|
R |
I∙Lн |
|
|
φн |
U |
|||||
|
I∙C |
I∙Rн |
|
|
|
∙ |
∙ |
|
|||||
|
|
|
|
|
|
|
|
|
|
∙ |
I |
|
|
|
|
|
|
АI |
|
||||||||
|
|
|
|
|
|
|
|
|
|
ILн |
∙ |
C |
|
|
|
|
|
|
|
|
|
|
|
|
Iн |
|
|
|
|
Рис. 2.17. Повышение коэффициента мощности: |
|||||||||||
|
|
а – схема замещения; б – векторная диаграмма |
|||||||||||
|
|
|
|
|
|
|
|
Д |
|||||
Если ток нагрузки Iн и коэффициент мощности приёмника cosφн |
|||||||||||||
известны и задано требуемое значение cosφ, то необходимое значение |
|||||||||||||
ёмкости конденсатора можно определить при помощи векторной диа- |
|||||||||||||
граммы токов (см. рис. 2.17, б), из которой следует, что |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
IRнtgϕн − IRнtgϕ = IC = ωCU , |
|
|
|||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
= |
|
P |
|
(tgϕн −tgϕ), |
|
(2.105) |
||
|
|
|
|
|
|
ωU 2 |
|
|
|
|
|
||
где Р – активная мощность приёмника, P = IRнU .
67
