
- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Матрицы. Операции над матрицами. Линейные преобразования и матрицы
Понятие матрицы было использовано нами в качестве вспомогательного инструмента при изучении систем линейных уравнений. Другие многочисленные применения сделали его предметом самостоятельной теории.
Матрицы
связаны естественным образом с линейным
преобразованием переменных. Под линейным
преобразованием переменных будем
понимать переход от одной системы
переменных
![]() к другой
к другой
![]() .
.
 (5.1)
(5.1)
Линейное преобразование задаётся посредством матрицы коэффициентов:
(5.2)
Def. Матрицей называется прямоугольная таблица, заполненная некоторыми математическими объектами, которые называются элементами матрицы.
Используется
также запись
![]() .
Напомним, что первый индекс нумерует
строки, а второй – столбцы.
.
Напомним, что первый индекс нумерует
строки, а второй – столбцы.
Матрицы обозначаются прописными латинскими буквами, а их элементы соответствующими строчными буквами с индексами.
Количество строк и столбцов определяет размер матрицы (об этом уже шла речь в лекции 1)
Def. Матрица, содержащая одну строку, называется матрицей-строкой (или вектор-строкой). Матрица, содержащая один столбец, называется матрицей-столбцом (или вектор-столбцом).
Def. Если все элементы матрицы равны 0, то такая матрица называется нулевой.
Def. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны 0, то матрица называется диагональной.
 (5.3)
(5.3)
Def. Диагональные матрицы, все элементы главной диагонали которых равны между собой, называют скалярными матрицами.
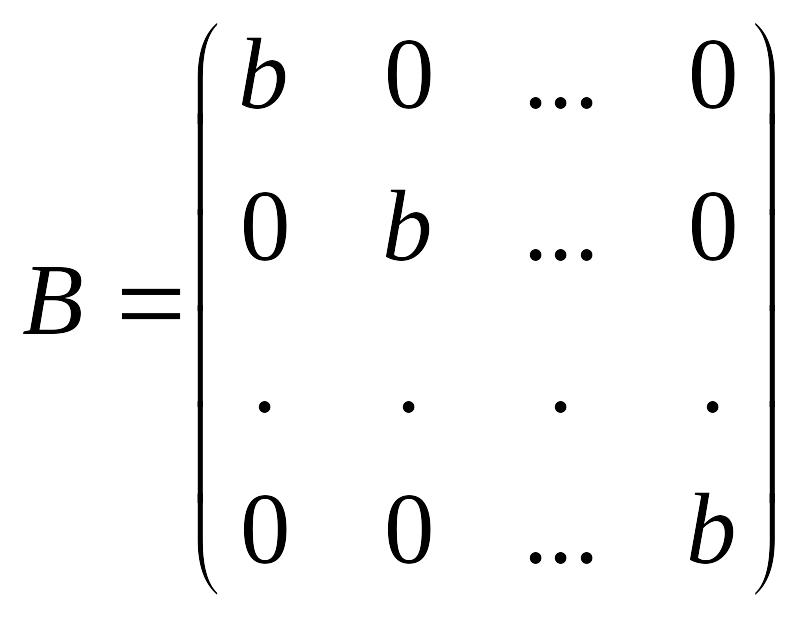 (5.4)
(5.4)
Def. Скалярная матрица, в которой все диагональные элементы равны 1, называется единичной матрицей.
 (5.5)
(5.5)
Def.
Две матрицы называются равными,
если равны их размерности и соответствующие
элементы, т.е.
![]()
Линейные операции над матрицами
Def.
Суммой
двух
матриц
и
![]() размерности
размерности
![]() называется
матрица
называется
матрица
![]() той же размерности, где
той же размерности, где
![]() .
.
N.
![]() .
.
Def.
Произведением
матрицы
на
число
называется матрица
![]() .
.
N.
![]() .
.
Def.
Матрица
![]() называется противоположной к матрице
и обозначается так:
называется противоположной к матрице
и обозначается так:
![]() .
.
Def.
Разность матриц
![]() определим как
определим как
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
Свойства линейных операций над матрицами.
|
Эти свойства непосредственно вытекают из соответствующих определений.
Нелинейные операции над матрицами
Def.
Произведением
строки
![]() на
столбец
на
столбец
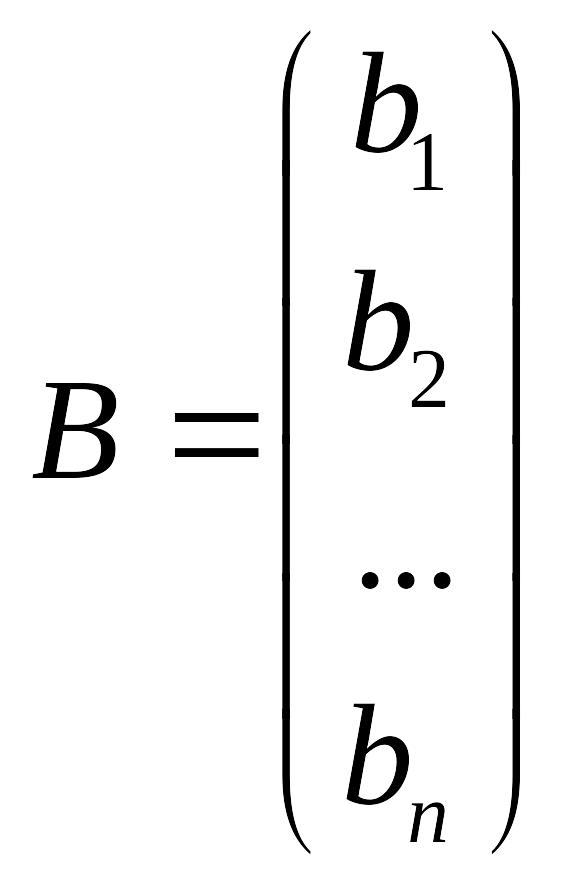 называется число равное
называется число равное
![]() .
.
Заметим, что произведение строки и столбца определено, если они имеют одинаковую длину.
Def. Матрицы называют согласованными, если число столбцов первой матрицы равно числу строк второй матрицы.
Для согласованных матриц определяют их произведение.
Def.
Произведением
матриц
![]() и
и
![]() называется матрица
называется матрица
![]() ,
где
,
где
![]() (5.6)
(5.6)
т.е.
элемент
![]() произведения определяется как произведение
i-ой
строки матрицы А
на j-ый
столбец матрицы В.
произведения определяется как произведение
i-ой
строки матрицы А
на j-ый
столбец матрицы В.
N

 .
.
![]()
![]() .
.
В примере
акцентируется внимание на нахождении
элемента
![]() матрицы-произведения. Для этого
перемножаются 1-я строка первого множителя
на 2-й столбец второго множителя.
матрицы-произведения. Для этого
перемножаются 1-я строка первого множителя
на 2-й столбец второго множителя.
Свойства произведения матриц:
|
Замечание. Эти свойства имеют место при условии, что все операции возможны.
Доказательство.
Для доказательства этого свойства достаточно привести контрпример.
Например,
показать, что
![]() .
.
Пусть
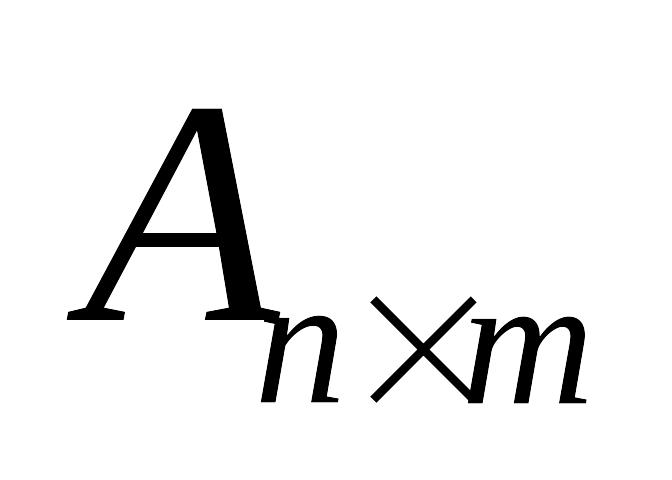 ,
,
 и
и
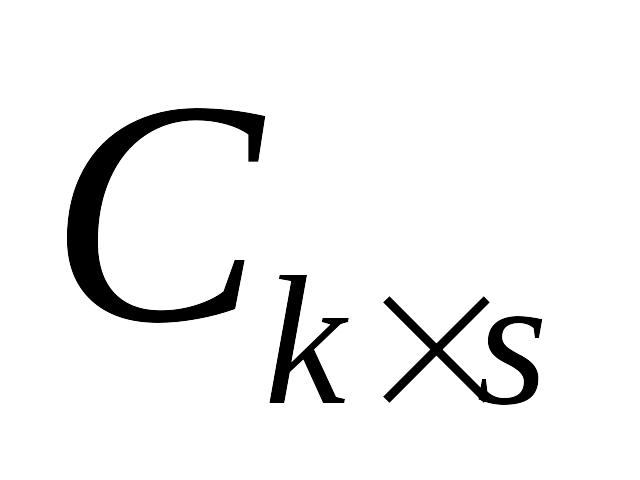 .
Тогда
.
Тогда
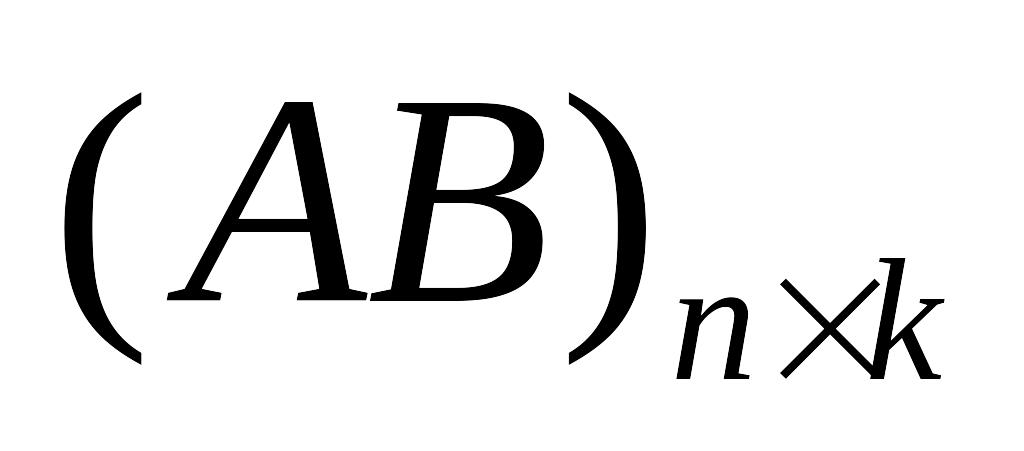 ,
а
,
а
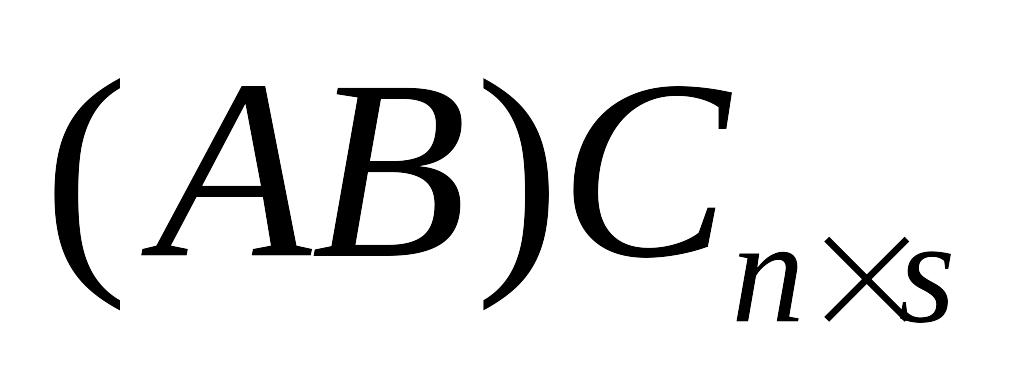 .
С другой стороны,
.
С другой стороны,
![]() ,
а
,
а
![]() .
Таким образом размерности матриц
.
Таким образом размерности матриц
![]() и
и
![]() одинаковы. Обозначим
одинаковы. Обозначим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Если теперь покажем, что
.
Если теперь покажем, что
![]() ,
то свойство доказано.
,
то свойство доказано.
![]() и
и
![]()
![]() и далее
и далее
![]() .
.
Заметим, что , т.к. они состоят из одних и тех же слагаемых, только расположенных в различном порядке .
Идея доказательства свойств 3 – 6 прозрачна, а потому не приводим их.
В лекции 3 определялась операция транспонирования матрицы (формула 3.1). Эта операция носит общий характер, т.е. применима к любой матрице. Справедливы следующие свойства:
|
Доказательство.
Свойства 1 – 3 проверяются непосредственно. Приведем доказательство свойства 4.
Пусть
и
.
Тогда
и
![]() .
С другой стороны,
.
С другой стороны,
![]() ,
,
![]() и
и
![]() .
Т.е. матрицы, стоящие в правой и левой
частях равенства, имеют одинаковую
размерность. Обозначим
,
.
Т.е. матрицы, стоящие в правой и левой
частях равенства, имеют одинаковую
размерность. Обозначим
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Покажем, что
.
.
Покажем, что
.
Имеем:
![]() ,
,
![]() .
.
С другой стороны,
![]() .
.
![]()
