Взаимное расположение прямых на плоскости

Пусть на координатной плоскости заданы две прямые и Исследуем их взаимное расположение на плоскости.

Две прямые на плоскости могут либо пересекаться (имеют единственную общую точку), либо параллельны (не имеют общих точек), либо совпадать (имеют бесконечное множество общих точек). Для нахождения точек пересечения прямых составим и исследуем СЛУ:

(13.15)

СЛУ (13.15) имеет единственное решение

СЛУ не имеет решений или

СЛУ имеет бесконечно много решений

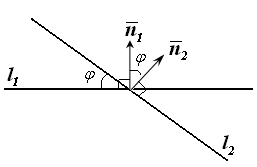
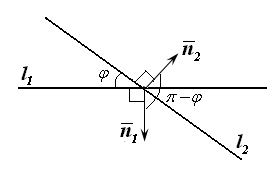
Взаимное расположение прямых на плоскости характеризуется также углом между прямыми. Он однозначно определяется углом между нормальными векторами этих прямых и , который обозначим через . Тогда:

(13.16)

Замечание. Обратим внимание, что угол между прямыми не обязательно равен , он может быть равен и (рис. 13.7-13.8). Таким образом, формула (13.16) определяет значение косинуса угла между прямыми с точностью до знака. Косинус острого угла между прямыми и может быть найден по формуле:

(13.17)

Заметим, что

Рис. 13.7

Рис. 13.8

Расстояние от точки до прямой

Пусть на координатной плоскости задана прямая и точка Найдем расстояние от точки до прямой Очевидно, что какова бы ни была точка прямой (рис. 13.9), справедливо соотношение:

Рис. 13.9

где

Поскольку то Тогда:

Таким образом, имеем:

(13.18)

Замечание. Если нормальный вектор прямой отложен от некоторой точки прямой, то для всех точек , которые лежат в одной полуплоскости с концом вектора , а для всех точек, лежащий в другой полуплоскости, Таким образом, для точек, лежащих в одной из полуплоскостей, на которые разбивает координатную плоскость прямая, а для точек другой полуплоскости

N. Какие из сторон треугольника АВС пересекает прямая если Найдите расстояние от точки А до прямой а.

Решение.

Подставим координаты точек А, В, С в левую часть уравнения прямой а.

А: ; В: ; С:

Значит, точки А и С лежат в одной полуплоскости относительно прямой а, а точка В в другой. Таким образом, прямая а пересекает стороны АВ и ВС треугольника АВС.

Ответ: прямая а пересекает стороны АВ и ВС;

Уравнение пучка прямых

Def. Пучком прямых на плоскости с центром в точке М называется множество всех прямых плоскости, проходящих через точку М (рис. 13.10). Отметим, что пучок задается однозначно либо своим центром, либо двумя пересекающимися прямыми.

Рис. 13.10

Th. 13.2

Если – центр пучка, то уравнение пучка имеет вид: (13.19) или (13.20)

Доказательство.

Доказательство вытекает непосредственно из формул (13.5) и (13.7). Заметим, что уравнение пучка (13.19) не содержит прямой

Th. 13.3

Если заданы две прямые и то уравнение пучка имеет вид: (13.21) Причем это уравнение содержит все прямые пучка, кроме

Доказательство.

1)Докажем, что уравнение (13.21) задает прямую пучка. Для любого уравнение (13.21) является уравнением первой степени, а значит, задает прямую.

Если – центр пучка, то и Значит, координаты удовлетворяют уравнению (13.21). Таким образом, прямая, задаваемая уравнением (13.21), принадлежит пучку.

2) Докажем, что в уравнении (13.21) всегда можно подобрать значение параметра так, чтобы прямая, определяемая этим уравнением, проходила через заданную точку т.е выполнялось соотношение:

Если то и значение однозначно определяется по формуле:

Если же, но то .

N. Составьте уравнение прямой, которая проходит через точку пересечения прямых и а) параллельно прямой б) перпендикулярно прямой

Решение.

Искомая прямая принадлежит пучку, который задается прямыми и Запишем уравнение пучка:

.

Или

а) Значение параметра найдем из условия параллельности искомой прямой и прямой

Отсюда:

Подставляя найденное значение параметра в уравнение пучка, получаем:

– искомая прямая.

б) Значение параметра найдем из условия перпендикулярности искомой прямой и прямой

Отсюда Подставляя найденное значение параметра в уравнение пучка, получаем уравнение искомой прямой:

Ответ: