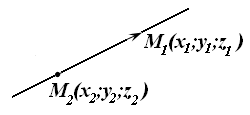- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
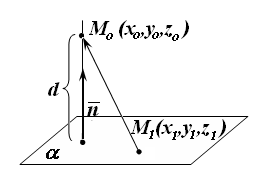
Расстояние от точки до плоскости
Пусть
в пространстве задана плоскость
где
|
Рис. 14.6 |
![]() Поскольку
Поскольку
![]() то
то
![]()
![]() Тогда:
Тогда:
![]()
Таким образом, имеем:
![]() (14.10)
(14.10)
Замечание.
Если нормальный вектор плоскости
отложен от некоторой точки прямой, то
для всех точек
,
которые лежат в одной полуплоскости с
концом вектора
,
а для всех точек, лежащий в другой
полуплоскости,
Таким образом, для точек, лежащих в одной
из полуплоскостей, на которые разбивает
координатную плоскость прямая,
![]() а для точек другой полуплоскости
а для точек другой полуплоскости
![]()
N.
Две грани куба лежат в плоскостях![]() и
и
![]() Найти объем куба.
Найти объем куба.
Решение.
Т.к.
![]() то
то
![]() Значит, в условии речь идет о противоположных
гранях куба. Ребро куба
равно расстоянию между этими плоскостями.
Для его нахождения выберем произвольную
точку плоскости
и вычислим расстояние от нее до плоскости
Значит, в условии речь идет о противоположных
гранях куба. Ребро куба
равно расстоянию между этими плоскостями.
Для его нахождения выберем произвольную
точку плоскости
и вычислим расстояние от нее до плоскости
![]()
Пусть
точка
![]() Значит, ее координаты удовлетворяют
уравнению плоскости
Значит, ее координаты удовлетворяют
уравнению плоскости
![]()
Найдем расстояние от точки до плоскости по формуле (14.10).
![]() Таким
образом,
Таким
образом,
![]() и
и
![]()
Ответ.
Пучок плоскостей
Def. Пучком плоскостей называют множество всех плоскостей, которые проходят через одну прямую , которую называют осью пучка.
Th. 14.2 |
Если
заданы две плоскости
Причем
это уравнение содержит уравнения всех
плоскостей пучка, кроме
|
Доказательство.
1)Докажем, что уравнение (14.11) задает плоскость пучка. Для любого уравнение (14.11) является уравнением первой степени, а значит, задает плоскость.
Если
–
произвольная точка оси пучка, то
![]() и
и
![]() Значит, координаты
удовлетворяют уравнению (14.11). Таким
образом, плоскость, задаваемая уравнением
(14.11), принадлежит пучку.
Значит, координаты
удовлетворяют уравнению (14.11). Таким
образом, плоскость, задаваемая уравнением
(14.11), принадлежит пучку.
2) Докажем, что в уравнении (14.11) всегда можно подобрать значение параметра так, чтобы плоскость, определяемая этим уравнением, проходила через заданную точку т.е выполнялось соотношение:
![]()
Если
![]() то
то
![]() и значение
однозначно определяется по формуле:
и значение
однозначно определяется по формуле:
![]() Если же,
Если же,
![]() но
но
![]() то
.
Таким образом, уравнение (14.11) не содержит
уравнения плоскости
.
то
.
Таким образом, уравнение (14.11) не содержит
уравнения плоскости
.
N.
Составить уравнение плоскости, которая
проходит через прямую пересечения
плоскостей
![]() и
и
![]() и точку
и точку
![]()
Решение.
Искомая плоскость – плоскость пучка, задаваемого уравнением
![]()
Отсюда
![]()
Поскольку
точка
![]() принадлежит этой плоскости, то
принадлежит этой плоскости, то
![]()
Откуда
![]() Подставляя значение
в уравнение пучка, получаем уравнение
искомой плоскости:
Подставляя значение
в уравнение пучка, получаем уравнение
искомой плоскости:
![]()
Ответ.
![]()
Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
Уравнение прямой в пространстве
Положение
прямой
в пространстве однозначно определяется
точкой
|
Рис. 15.1 |
прямой (рис. 15.1). тогда и только тогда, когда , т.е. или:
(15.1)
Уравнение (15.1) называется векторным уравнением прямой в пространстве. В координатной форме уравнение (15.1) записывается в виде:
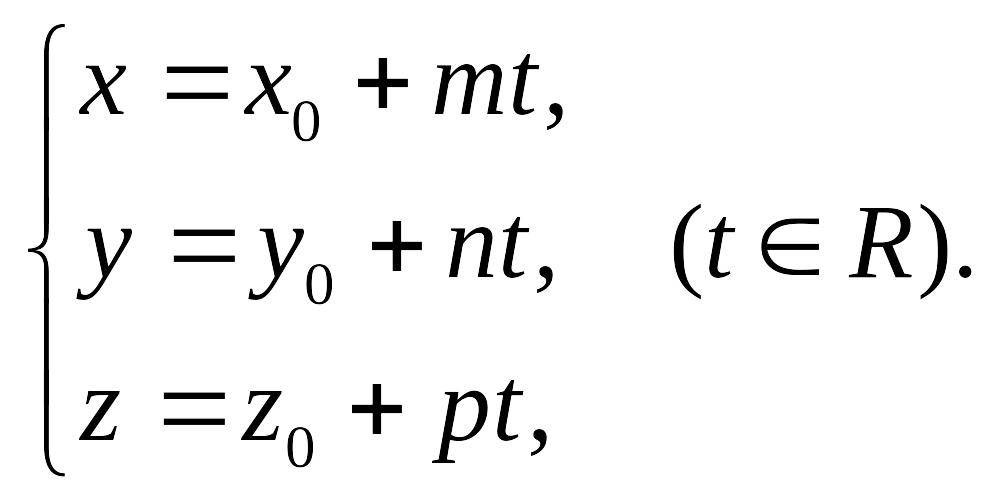 (15.2)
(15.2)
Уравнения (15.2) называют параметрическими уравнениями прямой в пространстве.
Условие можно записать в координатной форме:
![]() (15.3)
(15.3)
Уравнения (15.3) называют еще каноническими уравнениями прямой.
Замечание.
Если
![]() то уравнения (15.3) надо понимать в смысле
(15.2)
то уравнения (15.3) надо понимать в смысле
(15.2)
Прямая
также однозначно определяется двумя
точками
и
В этом случае в качестве направляющего вектора можно взять вектор
|
Рис. 15.2 |
Тогда уравнения (15.2) принимают вид:
![]() (15.4)
(15.4)
Уравнения (15.4) называют уравнениями прямой, проходящей через две точки.
Прямая
в пространстве может быть задана как
линия пересечения плоскостей. Пусть
плоскости
и
заданы соответственно уравнениями
![]() и
и
![]() Тогда их прямая пересечения может быть
задана следующим образом:
Тогда их прямая пересечения может быть
задана следующим образом:
![]() (15.5)
(15.5)
Очевидно,
для того, чтобы система (15.5) задавала
прямую необходимо и достаточно, чтобы
![]() и
и
![]() не были коллинеарны. В этом случае
направляющий вектор прямой
не были коллинеарны. В этом случае
направляющий вектор прямой
![]() определяется по формуле:
определяется по формуле:
![]() (15.6)
(15.6)
N.
Составить
канонические уравнения прямой
![]()
Решение.
Найдем
какую-нибудь точку на данной прямой.
Для этого положив
![]() получим систему:
получим систему:
![]()
Отсюда
![]() Таким
образом, точка
Таким
образом, точка
![]() - точка прямой.
- точка прямой.
Найдем направляющий вектор прямой по формуле (15.6).
![]()
![]() Тогда:
Тогда:
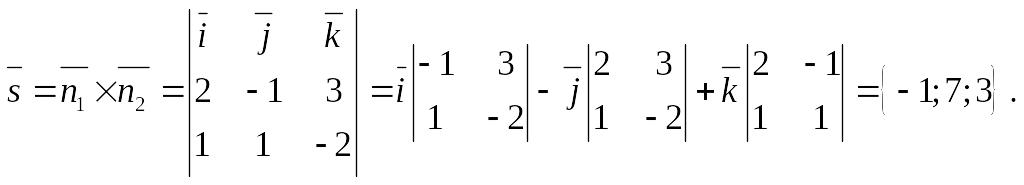
Составим канонические уравнения прямой, воспользовавшись формулой (15.3).
![]()
Ответ.
Замечание. Для составления канонических уравнений прямой можно поступить иначе. Можно отыскать две какие-нибудь точки данной прямой и воспользоваться уравнениями прямой, проходящей через две точки (15.4).