
- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Системы линейных уравнений
Рассмотрим систему линейных уравнений:
(7.6)
- матрица СЛУ (7.6), - расширенная матрица СЛУ(7.6).
Очевидно,
что
![]() .
Вопрос о совместности системы линейных
уравнений решается с помощью следующей
теоремы.
.
Вопрос о совместности системы линейных
уравнений решается с помощью следующей
теоремы.
Th.7.9 |
(Кронекера – Капелли) Система
линейных уравнений совместна тогда
и только тогда, когда
|
Доказательство.
Система линейных
уравнений несовместна тогда и только
тогда, когда в ступенчатой матрице к
которой сводится расширенная матрица
этой системы появляется строка вида
![]() ,
где
.
А это означает, что
,
где
.
А это означает, что
![]() .
Таким образом, система линейных уравнений
совместна тогда и только тогда, когда
.
.
Таким образом, система линейных уравнений
совместна тогда и только тогда, когда
.
|
Леопо́льд Кро́некер (7.12.1823 — 29.12.1891) — немецкий математик. Основные труды по алгебре и теории чисел. Большое значение имеют его исследования по арифметической теории алгебраических величин. |
Теорема Кронекера-Капелли утверждает существование решения СЛУ, но не указывает практического способа их отыскания. Укажем способ их нахождения.
Пусть
СЛУ (7.6) совместна, т.е.
![]() .
Пусть линейно независимыми являются
первые r
строк матрицы А
и первые r
строк матрицы
.
Пусть линейно независимыми являются
первые r
строк матрицы А
и первые r
строк матрицы
![]() Значит любая другая строка матрицы
является линейной комбинацией 1,2,…,r
строк. Тогда решение первых r
уравнений удовлетворяет остальным.
Таким образом, система (7.6) сводится к
системе (7.7):
Значит любая другая строка матрицы
является линейной комбинацией 1,2,…,r
строк. Тогда решение первых r
уравнений удовлетворяет остальным.
Таким образом, система (7.6) сводится к
системе (7.7):
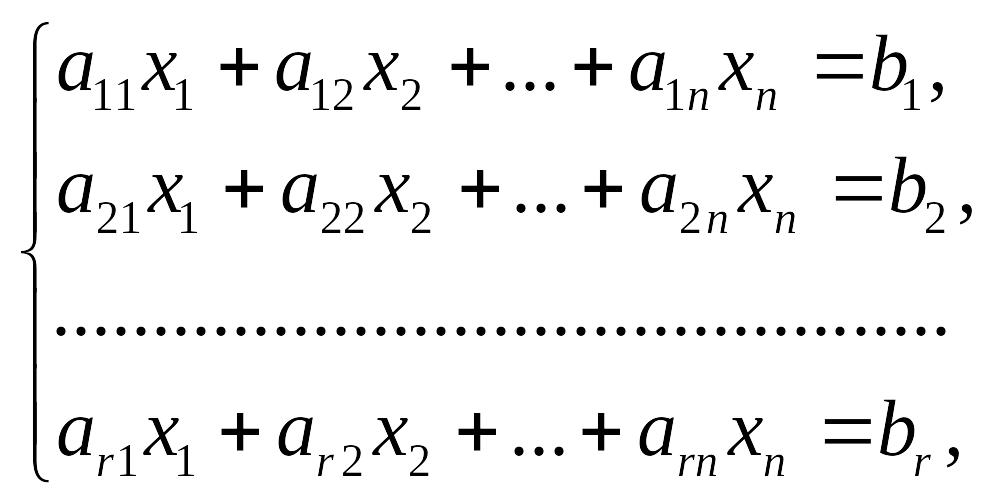 (7.7)
(7.7)
Если
![]() ,
то число уравнений равно числу неизвестных
и кроме того
.
Значит, согласно тереме Крамера, СЛУ
имеет единственное решение, которое
находится по формулам Крамера.
,
то число уравнений равно числу неизвестных
и кроме того
.
Значит, согласно тереме Крамера, СЛУ
имеет единственное решение, которое
находится по формулам Крамера.
Если
![]() ,
то число уравнений меньше, чем число
неизвестных и существует минор матрицы
А
r-го
порядка отличный от 0. Пусть он расположен
в первых r
столбцах. Оставим в левой части каждого
уравнения первые r
слагаемых, а остальные перенесем в
правую часть:
,
то число уравнений меньше, чем число
неизвестных и существует минор матрицы
А
r-го
порядка отличный от 0. Пусть он расположен
в первых r
столбцах. Оставим в левой части каждого
уравнения первые r
слагаемых, а остальные перенесем в
правую часть:
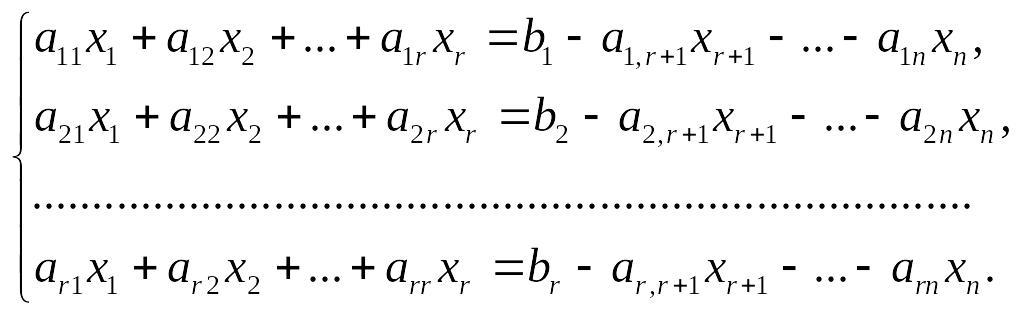 (7.8)
(7.8)
В СЛУ
(7.8) главный определитель
.
Если применить к (7.8) правило Крамера,
то она имеет единственное решение.
Значит, значения
![]() выбираем свободно (их называют свободные
переменные) и для каждого набора
выбираем свободно (их называют свободные
переменные) и для каждого набора
![]() найдем
найдем
![]() .
Таким образом, СЛУ имеет множество
решений.
.
Таким образом, СЛУ имеет множество
решений.
N.
Решить систему линейных уравнений
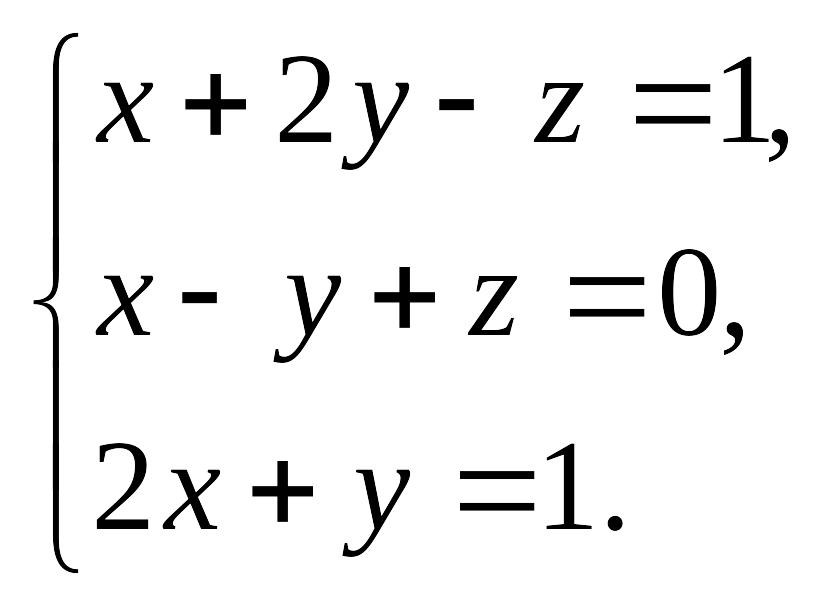 .
.
Решение.
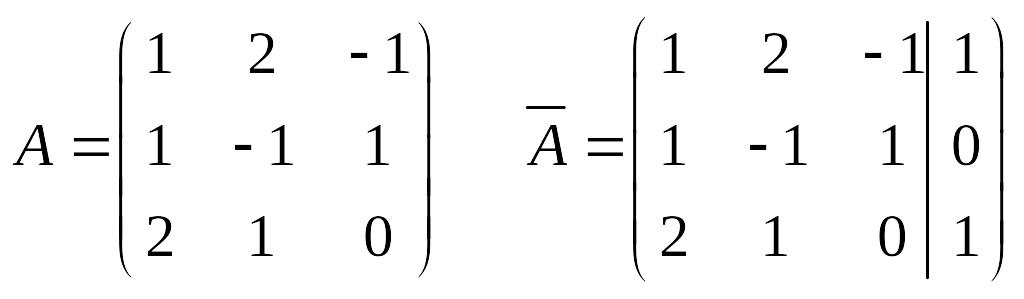 .
.
Данная
СЛУ имеет три неизвестные. Вычислим
ранги обеих матриц.
![]() .
Значит СЛУ совместна и имеет бесконечное
множество решений. Базисными строками
матриц А
и
являются первые две строки. Поэтому
оставим первые два уравнения системы,
а переменную z
считаем свободной и переносим ее в
правую часть уравнений:
.
Значит СЛУ совместна и имеет бесконечное
множество решений. Базисными строками
матриц А
и
являются первые две строки. Поэтому
оставим первые два уравнения системы,
а переменную z
считаем свободной и переносим ее в
правую часть уравнений:
![]() (7.9)
(7.9)
Решаем полученную систему по правилу Крамера.
![]() ,
,
![]() ,
,
![]() .
.
Откуда
![]() .
.
Ответ:
![]() .
.
Системы линейных однородных уравнений
Рассмотрим систему линейных однородных уравнений:
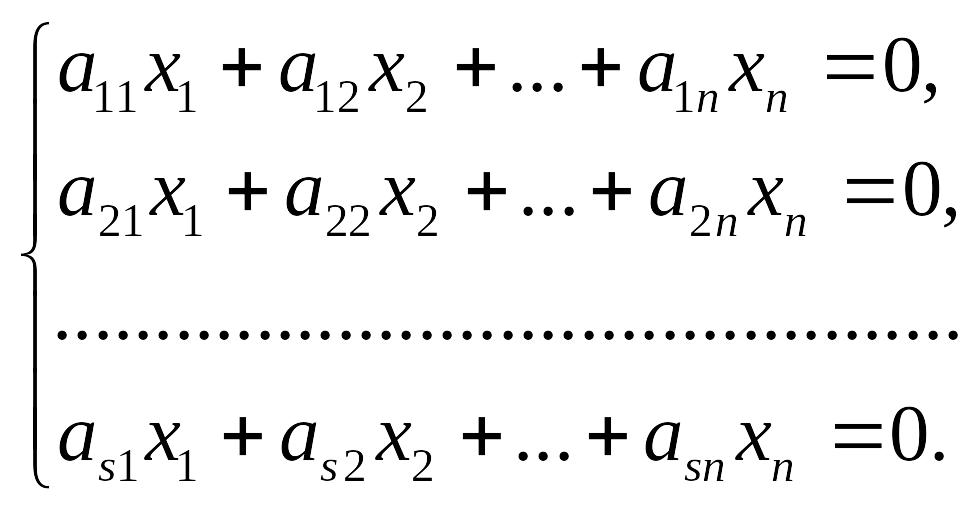 (7.9)
(7.9)
Очевидно,
что
![]() ,
т.к.
отличается от А
наличием
нулевого столбца. Значит, система
линейных однородных уравнений (СЛОУ)
всегда
,
т.к.
отличается от А
наличием
нулевого столбца. Значит, система
линейных однородных уравнений (СЛОУ)
всегда
совместна.
Пусть
![]() .
.
Если , то СЛОУ имеет единственное решение. Если - то множество решений.
Теорема 7.10 выражает свойства решений СЛОУ.
Th.7.10 |
Если
|
Доказательство.
СЛОУ
(7.9) запишем в матричном виде: АХ=0.
Т.к.
![]() - решение СЛОУ (7.9), то
- решение СЛОУ (7.9), то
![]() .
.
Рассмотрим
![]() .
Тогда
.
Тогда
![]() .
.
![]() Значит,
С
– решение СЛОУ (7.9)
.
Значит,
С
– решение СЛОУ (7.9)
.
Следствие 1. Множество решений СЛОУ образует линейное подпространство пространства . |
Def. Фундаментальной системой решений (ФСР) СЛОУ называется базис линейного подпространства ее решений.
Заметим, что СЛОУ имеет ФСР только в том случае, если она неопределенная. Причем таких ФСР бесконечное множество.
Th.7.11 |
(о ФСР СОЛУ) Пусть в СЛОУ (7.9) . Если , то ФСР СЛОУ состоит из n-r решений. |
Доказательство.
Пусть
- свободные переменные СЛОУ (7.9). Рассмотрим
произвольный определитель (n-r)-го
порядка
![]()
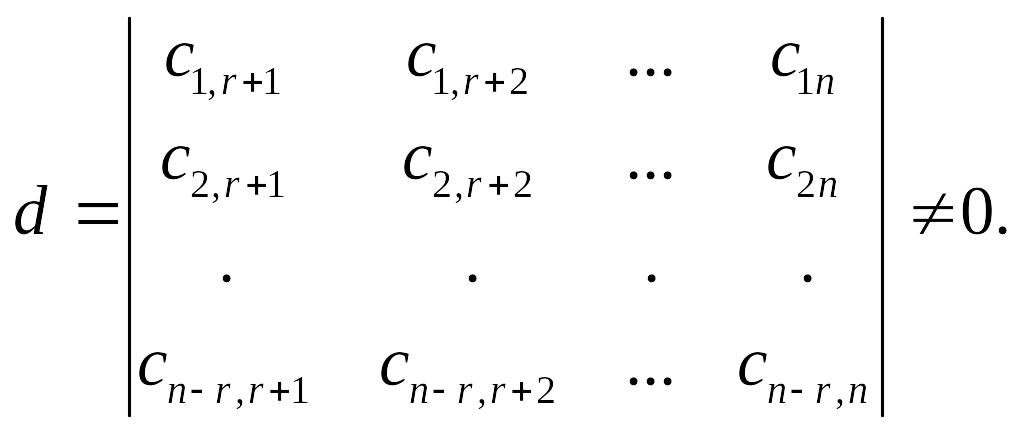 (7.10)
(7.10)
Выберем элементы определителя d в качестве свободных переменных, получим n-r решений СЛОУ (7.9):
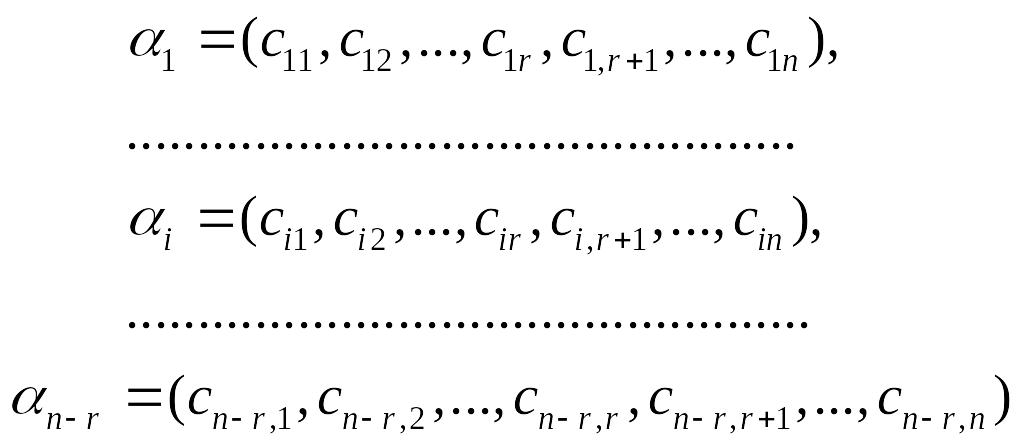 (7.11)
(7.11)
Покажем,
что
![]() – базис линейного подпространства
решений СЛОУ. Для этого необходимо
показать, что они линейно независимы и
любое другое решение СЛОУ является их
линейной комбинацией.
– базис линейного подпространства
решений СЛОУ. Для этого необходимо
показать, что они линейно независимы и
любое другое решение СЛОУ является их
линейной комбинацией.
n-мерные
векторы
– линейно независимы. Действительно,
если бы они были линейно зависимы, то
эта зависимость перенеслась бы и на
последние n-r
элементов,
т.е на строки определителя (7.10). Но тогда,
согласно критерию равенства нулю
определителя,
![]() а
это не так.
а
это не так.
Пусть
![]() – произвольное решение СЛОУ (7.9). Покажем,
что
– линейная комбинация
.
– произвольное решение СЛОУ (7.9). Покажем,
что
– линейная комбинация
.
Рассмотрим (n-r)-мерные векторы, компонентами которых служат строки определителя d:
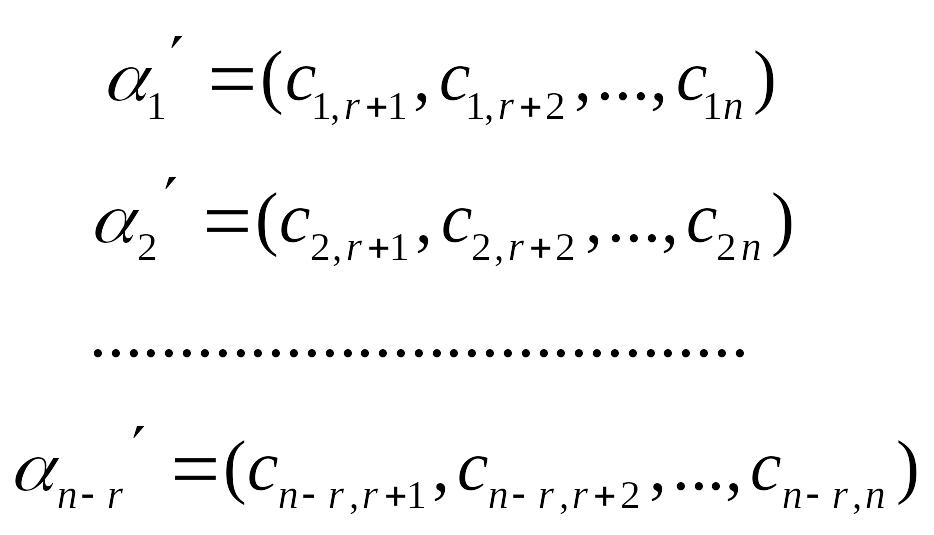 (7.12)
(7.12)
Векторы
![]() – линейно независимы, т.к.
Введем в рассмотрение еще один (n-r)-мерный
вектор
– линейно независимы, т.к.
Введем в рассмотрение еще один (n-r)-мерный
вектор
![]() (его компоненты совпадают с последними
n-r
компонентами вектора
).
(его компоненты совпадают с последними
n-r
компонентами вектора
).
Система
(n-r)-мерных
векторов
![]() –
линейно зависима согласно теореме 7.7.
Значит, на основании теоремы 7.6 можно
сделать вывод о том, что
–
линейно зависима согласно теореме 7.7.
Значит, на основании теоремы 7.6 можно
сделать вывод о том, что
![]() (7.13)
(7.13)
Рассмотрим
n-мерный
вектор
![]() .
На основании теоремы 7.10 можно утверждать,
что
.
На основании теоремы 7.10 можно утверждать,
что
![]() – решение СЛОУ (7.9). Из соотношения (7.13)
следует, что все компоненты вектора
,
соответствующие свободным переменным
равны 0. Но тогда
– тривиальное решение СЛОУ (7.9), т.е.
– решение СЛОУ (7.9). Из соотношения (7.13)
следует, что все компоненты вектора
,
соответствующие свободным переменным
равны 0. Но тогда
– тривиальное решение СЛОУ (7.9), т.е.
![]() .
Значит,
.
Значит,
![]() .
.
Таким образом, доказано, что образуют ФСР СЛОУ (7.9) .
Теорема 7.11 дает практический способ нахождения ФСР для СЛОУ: свободным переменным придают значения элементов (по строкам) любого определителя (n-r)-го порядка, отличного от нуля. Полученные при этом решения СЛОУ образуют ФСР. В качестве указанного определителя удобно брать определитель единичной матрицы (n-r)-го порядка.
N.
Найти
ФСР для СЛОУ
![]()
Решение.
![]() – свободные переменные.
– свободные переменные.
![]()
Придавая
свободным переменным значения элементов
по строкам определителя
![]() ,
вычисляем соответствующие значения
связных переменных.
,
вычисляем соответствующие значения
связных переменных.
|
|
|
|
-3 |
2 |
1 |
0 |
3 |
-4 |
0 |
1 |
Ответ:
![]() – ФСР.
– ФСР.
Рассмотрим связь, которая существует между решениями однородных и неоднородных систем. Путь дана система линейных неоднородных уравнений (СЛНУ):
(7.14)
Def. СЛОУ, полученная из системы (7.14) заменой свободных членов нулями, называется приведенной системой для СЛНУ.
Так СЛОУ (7.9) является приведенной для СЛНУ (7.14).
Следующие две теоремы отражают связь между решениями этих систем.
Th.7.12 |
Сумма любого решения СЛНУ (7.14) и приведенной системы (7.9) снова будет решением СЛНУ (7.14) |
Доказательство.
Запишем обе системы в матричном виде:
(7.14)
![]() АХ=В
АХ=В
(7.9) АХ=0
Пусть С – решение СЛНУ (7.14), а Р – решение СЛОУ (7.9). Тогда АС=В и АР=0.
А(С+Р)=АС+АС=В+0=В. Т.е. Р+С – решение СЛНУ (7.14) .
Th.7.13 |
Разность двух решений СЛНУ (7.14) есть решение СЛОУ (7.9) |
Доказательство.
Запишем обе системы в матричном виде:
(7.14) АХ=В
(7.9) АХ=0
Пусть
![]() и
и
![]() - решения СЛНУ (7.14). Тогда
- решения СЛНУ (7.14). Тогда
![]()
![]()
![]() – решение
СЛОУ (7.9)
.
– решение
СЛОУ (7.9)
.
![]()

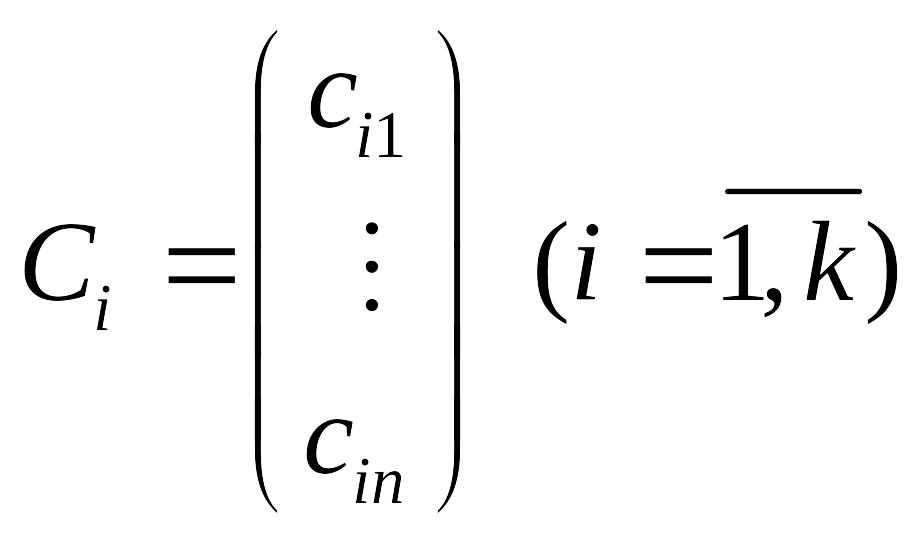 –
решение СЛОУ (7.9), то любая их линейная
комбинация является решением СЛОУ
(7.9).
–
решение СЛОУ (7.9), то любая их линейная
комбинация является решением СЛОУ
(7.9).