- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Декартова система координат. Координаты вектора
Def.
Афинной
системой
координат
в пространстве
называется совокупность точки, называемой
началом координат, и базиса
![]()
Def.
Если
![]() то система координат называется
декартовой
системой координат.
то система координат называется
декартовой
системой координат.
Def.
Координатами
точки
в аффинной системе координат называются
координаты ее радиус вектора
![]() (рис. 10.12).
(рис. 10.12).
Таким
образом, если
![]() то
то
![]()
Def.
Если из конца
вектора
![]() поворот от
поворот от
![]() к
к
![]() виден против часовой стрелки, то
виден против часовой стрелки, то
![]() называют правой
тройкой
векторов, а соответствующую систему
координат называют правой
системой координат
(рис. 10.13). Если же такой поворот виден
по часовой стрелке, то
называют левой
тройкой векторов,
а соответствующую систему координат
левой
системой координат
(рис. 10.14).
называют правой
тройкой
векторов, а соответствующую систему
координат называют правой
системой координат
(рис. 10.13). Если же такой поворот виден
по часовой стрелке, то
называют левой
тройкой векторов,
а соответствующую систему координат
левой
системой координат
(рис. 10.14).
Def.
Если
![]() и
и
![]() то базис
называется ортонормированным, а
соответствующая система координат –
прямоугольной
декартовой системой координат.
то базис
называется ортонормированным, а
соответствующая система координат –
прямоугольной
декартовой системой координат.
Рис. 10.12 |
Рис. 10.13 |
Рис. 10.14
|
Базис
прямоугольной декартовой системы
координат принято обозначать
![]() (рис. 10. 15).
(рис. 10. 15).
Таким
образом, если в прямоугольной декартовой
системе координат
![]() то ее радиус-вектор
то ее радиус-вектор
![]() имеет следующее разложение:
имеет следующее разложение:
Оси
сонаправленные с базисными векторами
называют координатными осями абсцисс,
ординат и аппликат соответственно
(
Найдем
координаты вектора если известны
координаты его начала и его конца.
Пусть
|
|
![]() (10.10)
(10.10)
Пусть
заданы
,
и некоторая точка
![]() которая
делит отрезок АВ
в отношении m:n,
считая от точки А,
т.е.
которая
делит отрезок АВ
в отношении m:n,
считая от точки А,
т.е.
![]() Найдем
координаты точки
Найдем
координаты точки
![]()
Очевидно,
что
![]()
![]()
![]()
Получаем:
![]()
![]()
Отсюда
![]()
![]() Аналогично
находим
Аналогично
находим
![]() и
и
![]() Таким образом,
Таким образом,
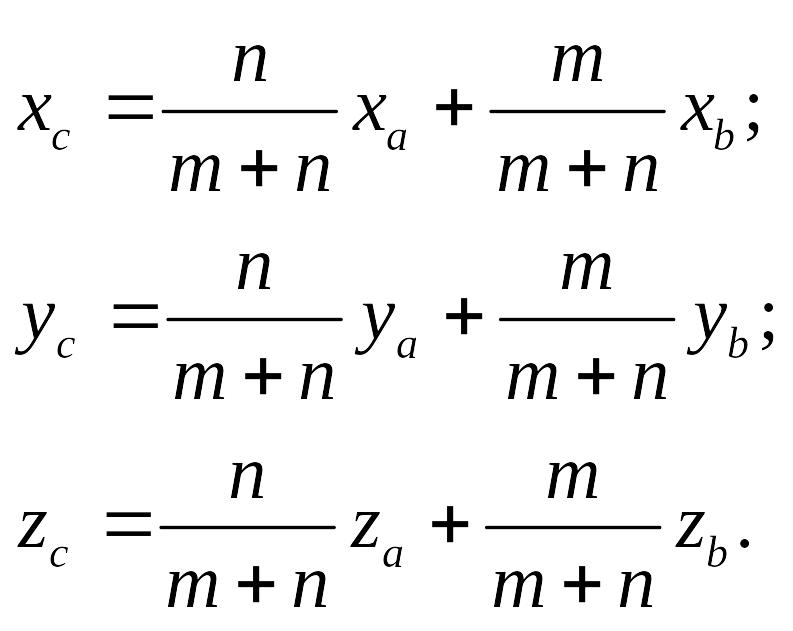 (10.11)
(10.11)
Формулы (10.11) носят название формул деления отрезка в заданном отношении.
![]()
Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
Def.
Прямая
называется осью,
если на ней задано положительное
направление.
Направление оси задается вектором
![]() (направляющий вектор оси).
(направляющий вектор оси).
Def.
Пусть
задана некоторая ось
и
точка
![]() Проведем
Проведем
![]() Точка
Точка
![]() называется проекцией
точки
на ось
(рис. 11.1)
называется проекцией
точки
на ось
(рис. 11.1)
Def.
Пусть
- проекция точки
на
ось
![]() а
а
![]() - проекция точки
на
ось
(рис. 11.2)
Тогда
- проекция точки
на
ось
(рис. 11.2)
Тогда
![]() называется векторной
проекцией
на ось
(на вектор
).
называется векторной
проекцией
на ось
(на вектор
).
Def.
Скалярной
проекцией
(или проекцией) вектора
на ось
(на вектор
)
называется число, равное
![]() и взятое со знаком плюс, если
и взятое со знаком плюс, если
![]() и со знаком минус, если
и со знаком минус, если
![]() Обозначают
Обозначают
![]() или
или
![]() .
Т.е.
.
Т.е.
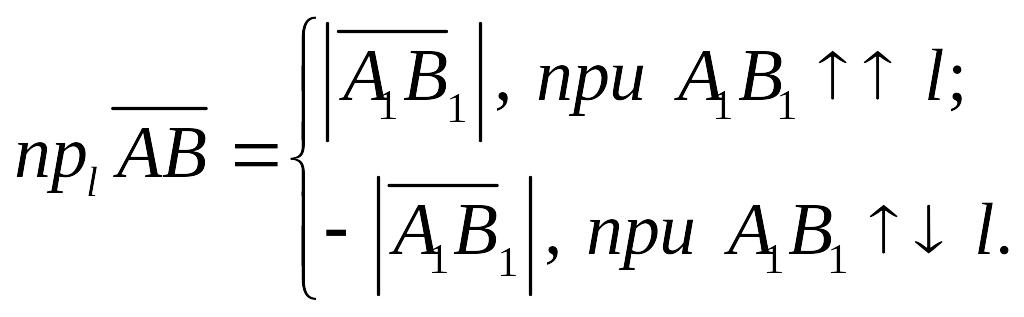 (11.1)
(11.1)
Легко видеть, что
![]() если
если
![]()
Рис. 11.1 |
|
Рис. 11.3 |
Th.11.1 |
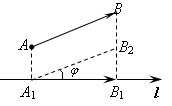
(свойства проекции вектора на ось) 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью, т.е.
2. При умножении вектора на число его проекция на ось также умножается на это число, т.е.
3. Проекция суммы векторов на ось равна сумме проекций слагаемых, т.е.
|
Доказательство.
1.
Действительно,
пусть
![]() уго между
и
уго между
и
![]() Если
Если
![]() (рис. 11.3),
то
(рис. 11.3),
то
![]() ,
поэтому
,
поэтому
![]()
Если
|
Рис. 11.4 |
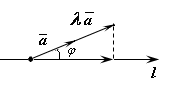
2.
Если
![]() то
то
![]() (рис. 11.5). Тогда:
(рис. 11.5). Тогда:
![]() .
.
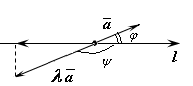
Если
![]() то
то
![]() (рис. 11.6). В этом случае имеем:
(рис. 11.6). В этом случае имеем:
![]() .
.
Рис. 11.5 |
Рис. 11.6 |
Рис. 11.7 |
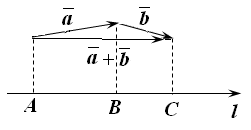
3. Доказательство проведем для двух слагаемых. Возможны два случая.
Если
проекции обоих векторов положительные
числа (рис. 11.7), то
![]() .
.
Если
одна из проекций отрицательна (рис.
11.8), то
Замечание. Данное свойство можно обобщить на любое конечное число слагаемых. |
Рис. 11.8 |

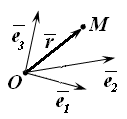
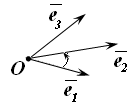
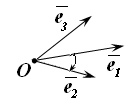
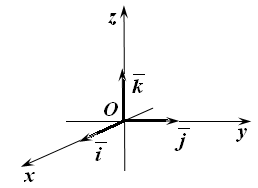 Рис.
10.15
Рис.
10.15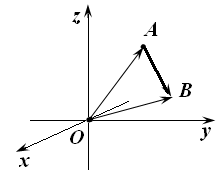 Рис.
10.16
Рис.
10.16
 Рис.
11.2
Рис.
11.2