Подстановки

Def. Подстановкой степени n называется взаимно однозначное отображение множества чисел 1, 2, 3, …, n на себя.

Записывают подстановку в виде двух перестановок, записанных друг под другом:

(2.1)

Подстановка обладает многими различными записями вида (2.1). Любая подстановка А может быть записана в виде:

(2.2)

Здесь - перестановка чисел 1, 2, 3, …, n.

Очевидно, что общее число подстановок степени n равно

Def. Подстановка называется четной (нечетной), если общее число инверсий в перестановках, образованных в верхней и нижней строках четно (нечетно).

Если подстановка записана в виде (2.2), то ее четность определяется четностью перестановки во второй строке, поскольку число инверсий в верхней строке равно нулю.

Def. Транспозицией подстановки называется транспозиция одной из перестановок в верхней или нижней строках (но не в обоих одновременно).

Отсюда следует, что всякая транспозиция меняет четность подстановки на противоположную. Число четных подстановок степени n равно числу нечетных подстановок и равно .

Очевидным является следующее утверждение.

Th.2.4

Транспозиция любых столбиков в подстановке не меняет ее четности .

Def. Подстановка называется тождественной.

Def. Применение одной подстановки вслед за другой тоже будет подстановкой, которую называют произведением первой из заданных подстановок на другую.

N. Пусть и . Найти и . , .

Свойства произведения подстановок:

1. Произведение подстановок некоммутативно, т.е. . 2. Произведение подстановок ассоциативно, т.е. . 3. Произведение любой подстановки на тождественную , а также произведение тождественной подстановки на равно .

Доказательство.

1) Доказательством некоммутативности является приведенный выше пример.

2) Докажем ассоциативность произведения подстановок. Пусть (подстановка А переводит элемент в элемент ), , . Тогда, , а . С другой стороны и .

3) Если и , то, перемножая эти подстановки, получаем, что .

Def. Обратной для подстановки А называется такая подстановка той же самой степени, что .

Очевидно, что для подстановки обратная получается переменой строк, т.е.

. (2.3)

С каждой квадратной матрицей 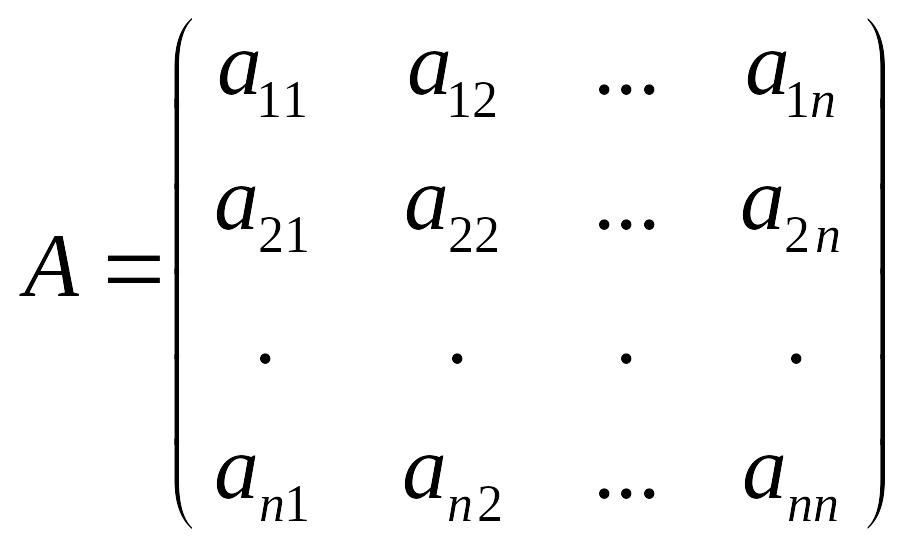связано определенное число, называемое ее определителем или детерминантом, которое обозначается (или ) и записывается в следующей символьной форме:

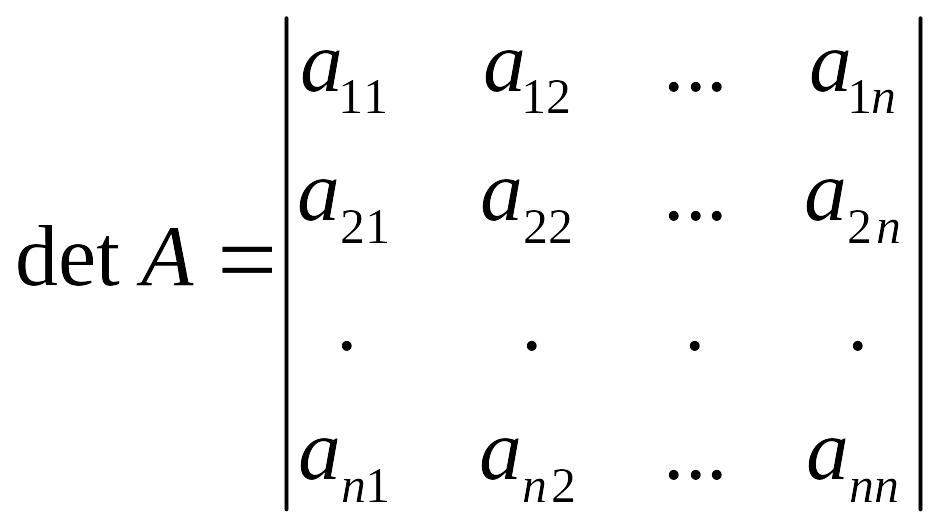(2.4)

Определитель n-го порядка

Def. Определителем n-го порядка называется число, равное алгебраической сумме слагаемых, каждое из которых представляет произведение множителей, взятых по одному и только по одному из каждой строки и каждого столбца. Причем каждое слагаемое входит в сумму со знаком «+», если подстановка, состоящая из индексов множителей четная, и со знаком «–», если эта подстановка нечетная, т.е.:

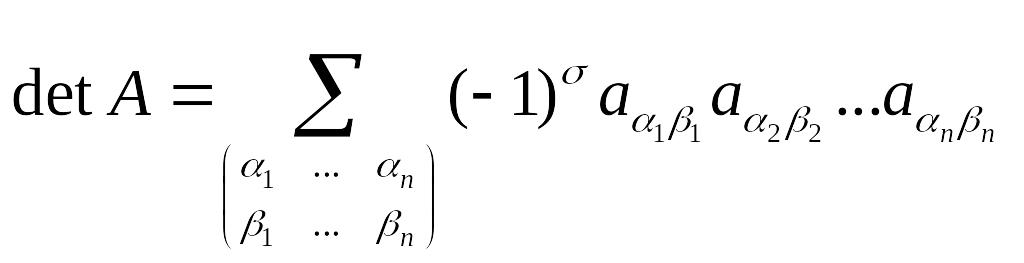(2.5)

или

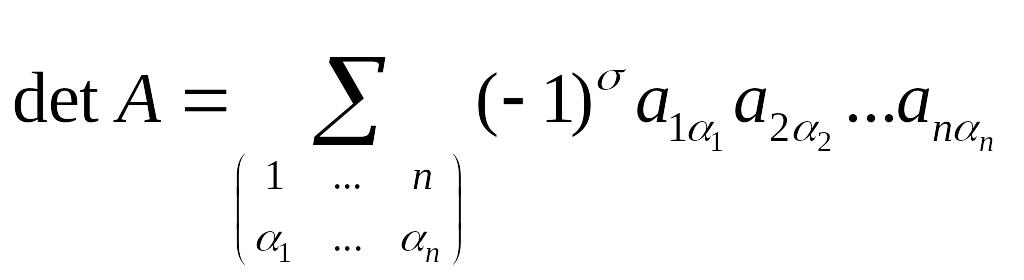, (2.6)

где – общее число инверсий в обеих строках подстановки.

В частности, определитель второго порядка будет содержать два слагаемых: и . Определим знаки этих слагаемых. Подстановка из индексов слагаемого имеет вид и является четной. Значит, это слагаемое входит в определитель со знаком «+». Подстановка из индексов, соответствующая слагаемому имеет вид и является нечетной. Т.е. второе слагаемое входит в определитель со знаком «–». Таким образом,

(2.7)

Т.е. определитель второго порядка равен разности произведения элементов главной диагонали и элементов побочной диагонали.

Аналогично, определитель третьего порядка содержит 3!=6 слагаемых и вычисляется по формуле:

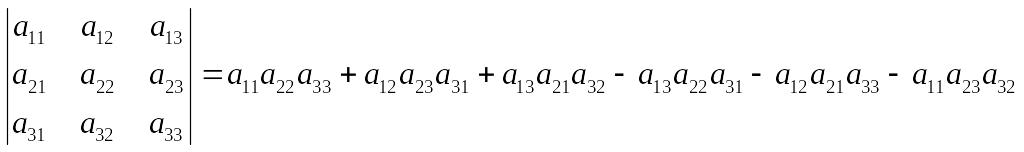(2.8)

Убедитесь самостоятельно в правильности знаков слагаемых в формуле (2.8). Для запоминания этой формулы используют схему:

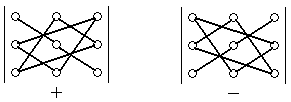
Рис. 2.1. Схема вычисления определителя третьего порядка

Существует удобный способ вычисления определителя третьего порядка с помощью так называемого правила Саррюса. Допишем справа к определителю первые два столбца, а далее будем перемножать элементы, стоящие на одних диагоналях так, как показано на рисунке 2.2.

– – – + + + Рис. 2.2 Правило Саррюса для вычисления определителя третьего порядка

Вычисление определителей более высоких порядков по определению представляется очень громоздким. Уже определитель 4-го порядка будет содержать 4!=24 слагаемых, а определитель 5-го порядка уже 5!=120 слагаемых. Далее мы сформулируем свойства определителей, которые облегчат их вычисление.