Вычисление определителей

Сформулированные свойства определителей порождают методы их вычисления.

1.Метод Гаусса.

Этот метод заключается в том, что сначала определитель приводят к верхнетреугольному виду, а затем применяют теорему об определителе верхнетреугольной матрицы.

Пьер-Симо́н Лапла́с (23.03.1749 — 5.03.1827) — выдающийся французский математик, физик и астроном; известен работами в области небесной механики, дифференциальных уравнений, один из создателей теории вероятностей. Заслуги Лапласа в области чистой и прикладной математики громадны: он усовершенствовал почти все разделы этих наук.

N. Вычислить определитель

Решение.

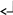
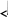
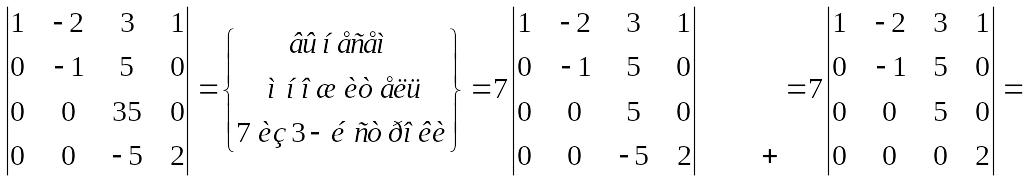
2. На основании теоремы Лапласа.

Теорема Лапласа (о разложении определителя по строке или столбцу) позволяет свести вычисление n-го порядка к вычислению нескольких определителей порядка (алгебраических дополнений). Особенно удобно использовать разложение по тем строкам (или столбцам), в которых есть нулевые элементы.

N. Вычислить определитель

Решение.

Разложим определитель по элементам второго столбца:

, , .

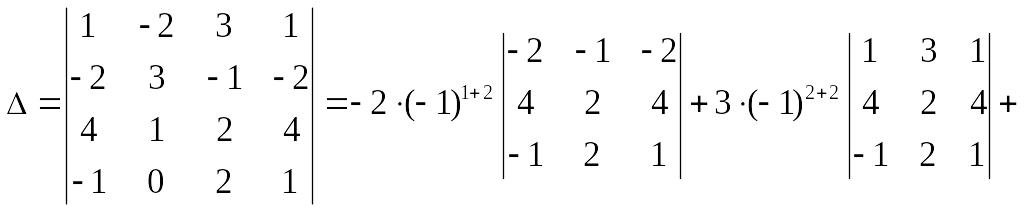
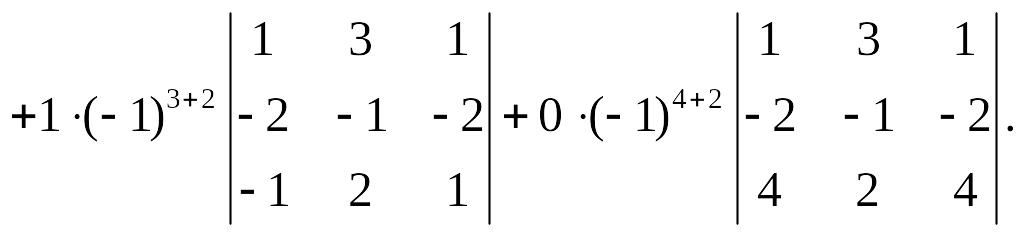
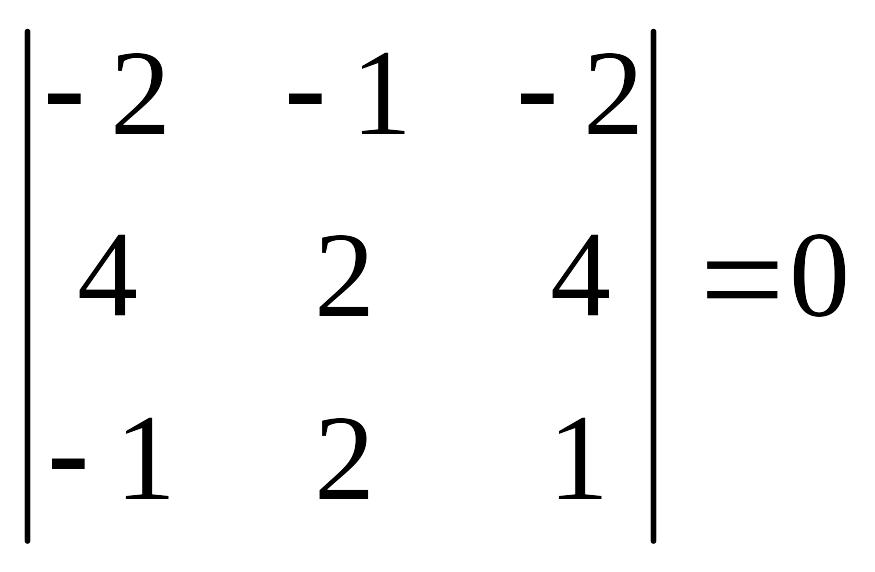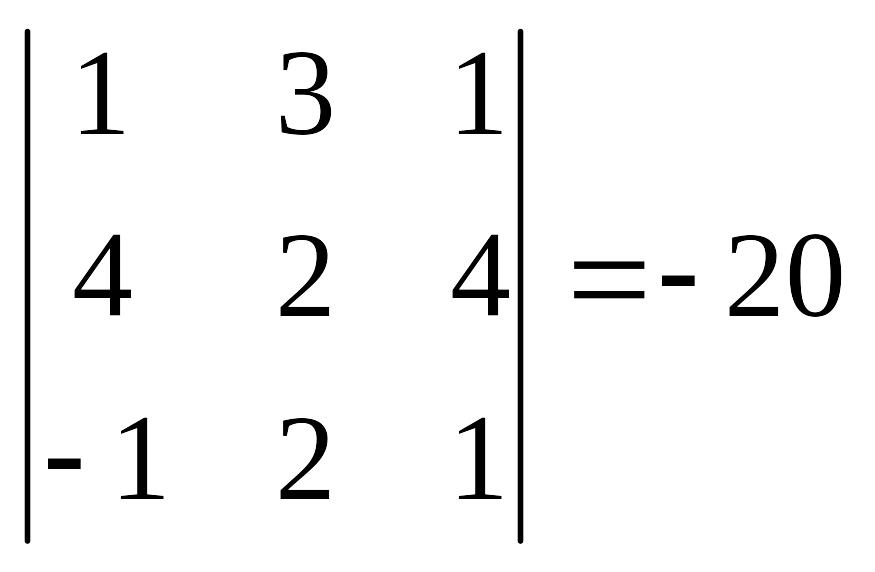Значит,

3. Метод рекуррентных (возвратных) соотношений.

Пусть дан определитель определенной структуры. Если удается выразить его через определитель такой же структуры, но меньшего порядка, то говорят, что получено рекуррентное соотношение ( ).

На основании этого соотношения, выражая через , …, через , получают значение определителя.

N. Вычислим определитель Вандермонда .

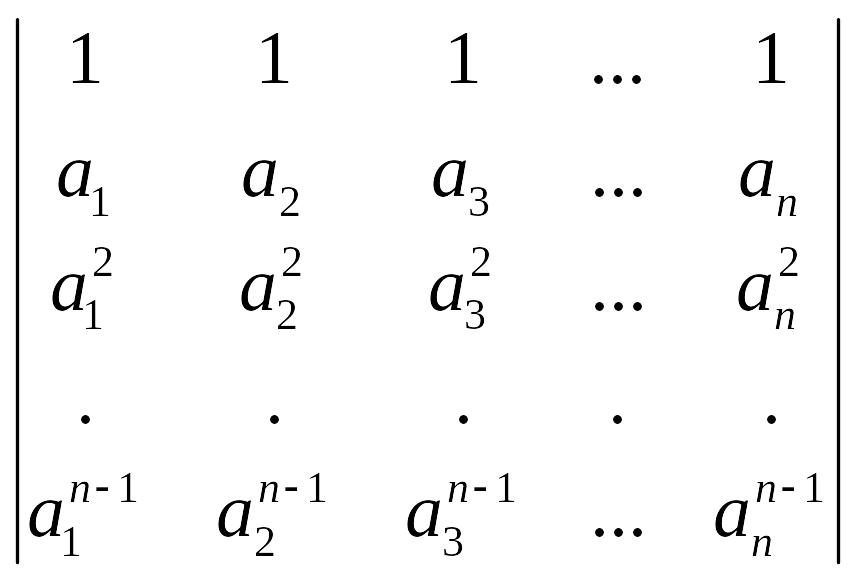Решение.

Вычтем из каждой строки предыдущую, умноженную на :

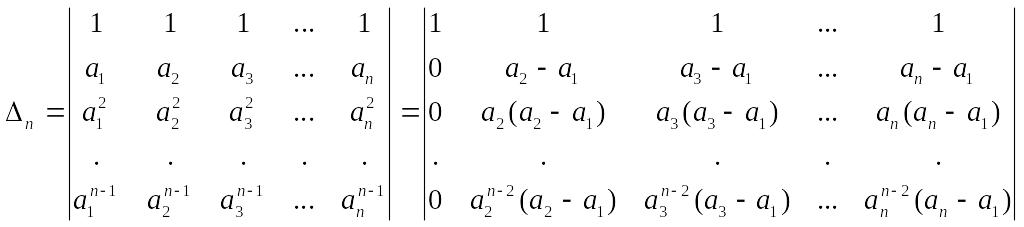
Разложим определитель по элементам первого столбца:

.

Теперь можно вынести из первого столбца общий множитель , из второго – и т.д., из последнего – . Имеем:

.

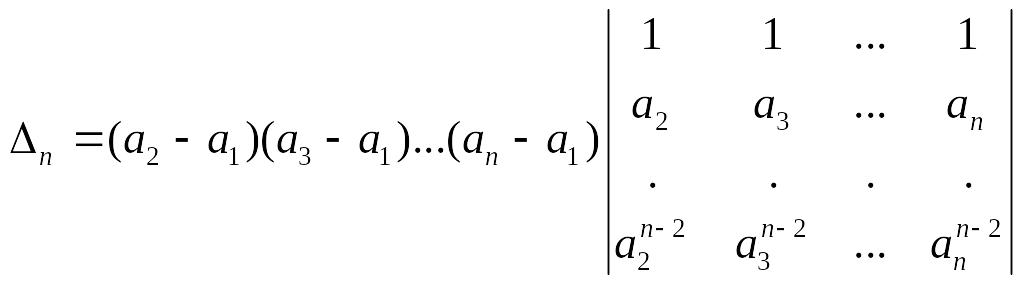Стоящий в правой части определитель также является определителем Вандермонда порядка , т.е.:

.

Поступим с этим определителем аналогичным образом. Получим:

.

Продолжая аналогичные рассуждения, окончательно имеем:

Правило Крамера.

Теория определителей имеет широкое применение в теории систем линейных уравнений.

Lemma

Сумма произведений элементов любой строки (столбца) на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Доказательство.

Пусть дан определитель .

Габриэ́ль Кра́мер (31.07.1704 — 4.01.1752)  — швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры. Заложил основы теории определителей. Ему принадлежат также исследования по теории алгебраических кривых высших порядков.

Рассмотрим другой определитель , отличающийся от только тем, что в k-ом столбце повторен i-ый столбец.

.

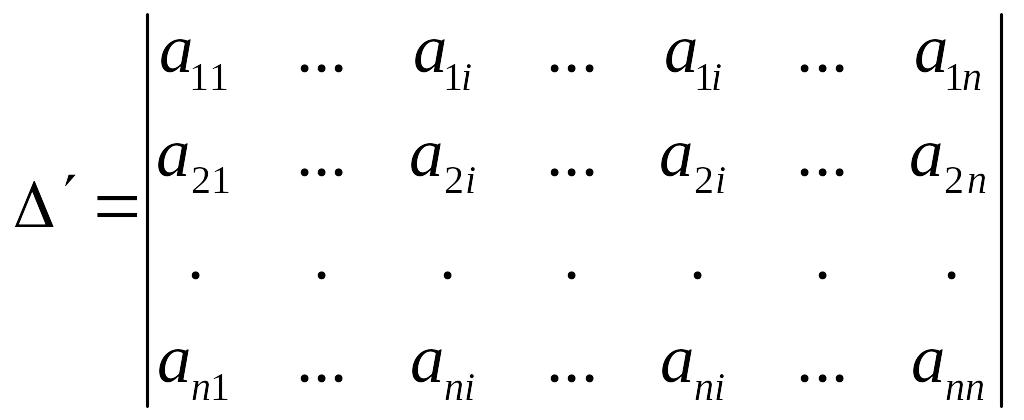По теореме 3.4 . Разложим его по элементам k-го столбца, получим:

, где - алгебраические дополнения к элементам k-го столбца определителя . Но поскольку отличается от только k-ым столбцом, то они будут и алгебраическими дополнениями элементов k-го столбца и в определителе . Таким образом.

.

Рассмотрим систему n линейных уравнений с n неизвестными:

(4.3)

Назовем определитель матрицы СЛУ (4.3) главным определителем этой системы. Умножим первое уравнение на , второе – на и т.д., n-ое уравнение – на и сложим их. Имеем:

.

Согласно выше доказанной лемме , …, . В силу следствия из теоремы Лапласа о разложении определителя по элементам столбца , а 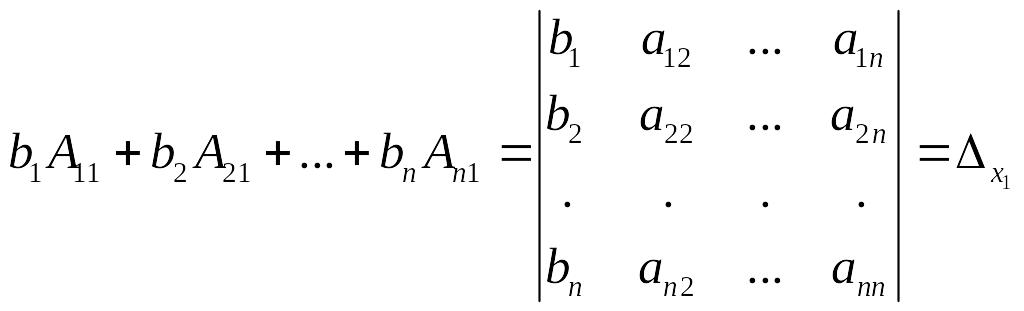- определитель, полученный из главного определителя СЛУ путем замены его первого столбца столбцом свободных членов. Таким образом, получили: (4.4)

Аналогично получаем: , …, (4.5)

1) Если , то СЛУ (4.3) имеет единственное решение:

(4.6)

Формулы (4.6) называются формулами Крамера.

2) Если , а хотя бы один из , то СЛУ (4.3) несовместна.

3) Если , то СЛУ (3.9) неопределенна или несовместна.