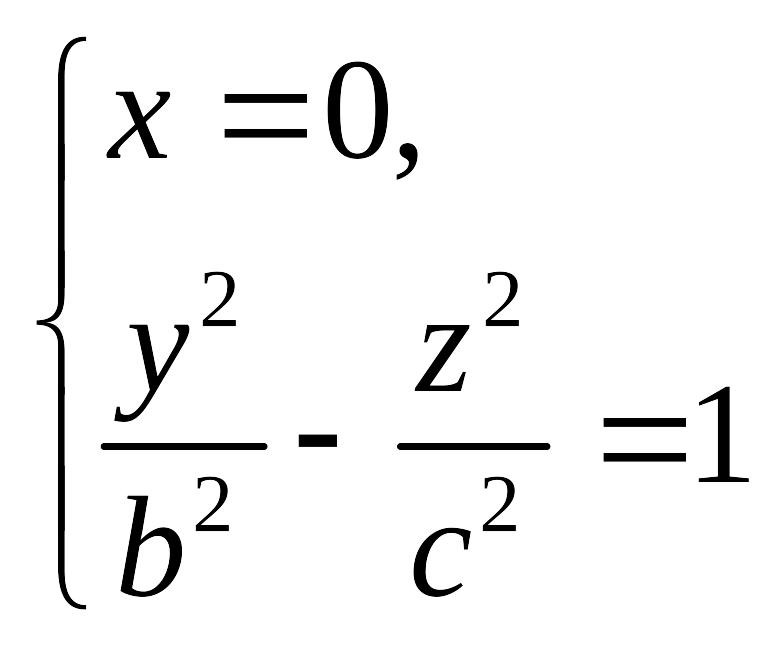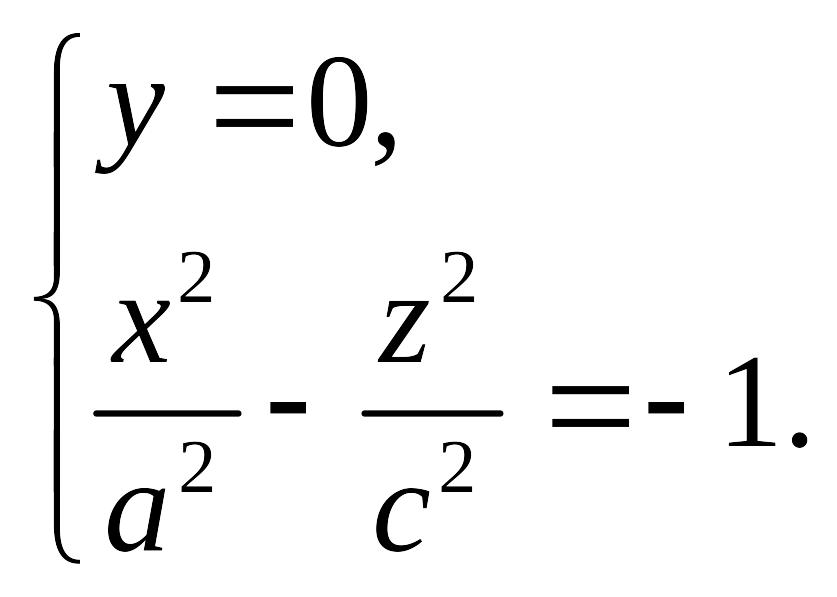- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
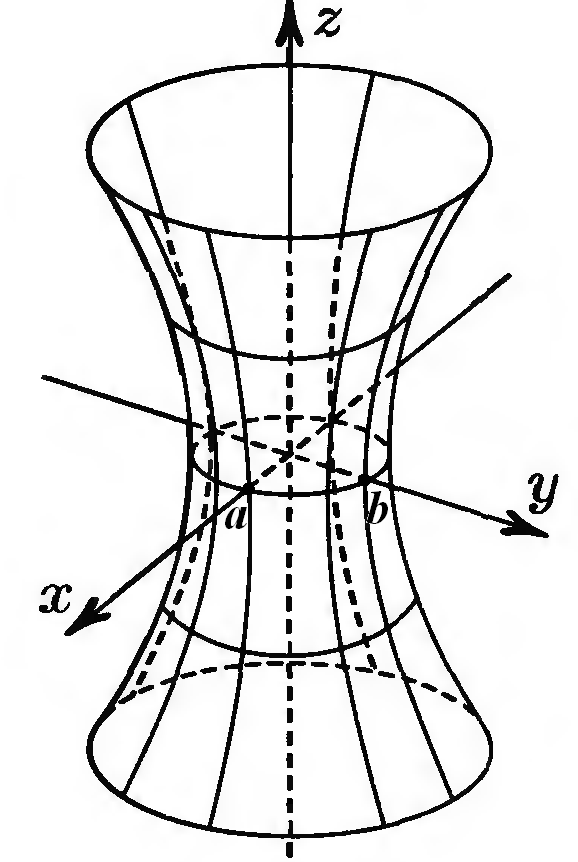
Однополостной гиперболоид
Def. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид:
(18.4)
Исследуем форму однополостного гиперболоида по той же схеме, по которой исследовали форму эллипсоида.
1. Из
уравнения (18.4) следует, что оси коодинат
являются осями симметрии однополостного
гиперболоида, координатные плоскости
– плоскостями симметрии, а начало
отсчета – центром симметрии. Ось
поверхность пересекает в точках с
координатами
![]() ось
в точках с координатами
ось
в точках с координатами
![]() точек пересечения с осью
точек пересечения с осью
![]() нет.
нет.
2. Линия
пересечения однополостного гиперболоида
с плоскостью
![]() имеет уравнение:
имеет уравнение:
Данная линия представляет собой эллипс с полуосями и
3.
Рассмотрим пересечение однополостного
гиперболоида и плоскости
![]() Линия пересечения задается уравнением
Линия пересечения задается уравнением
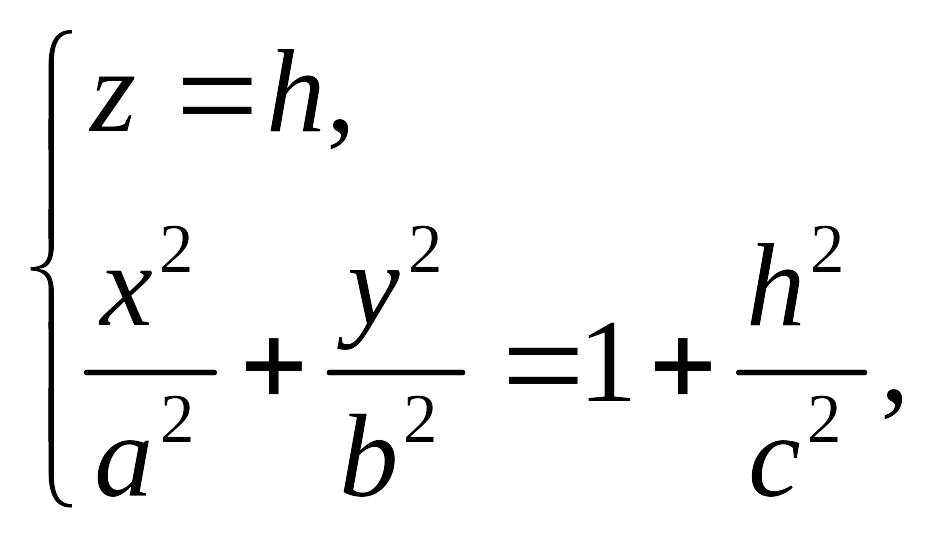
или
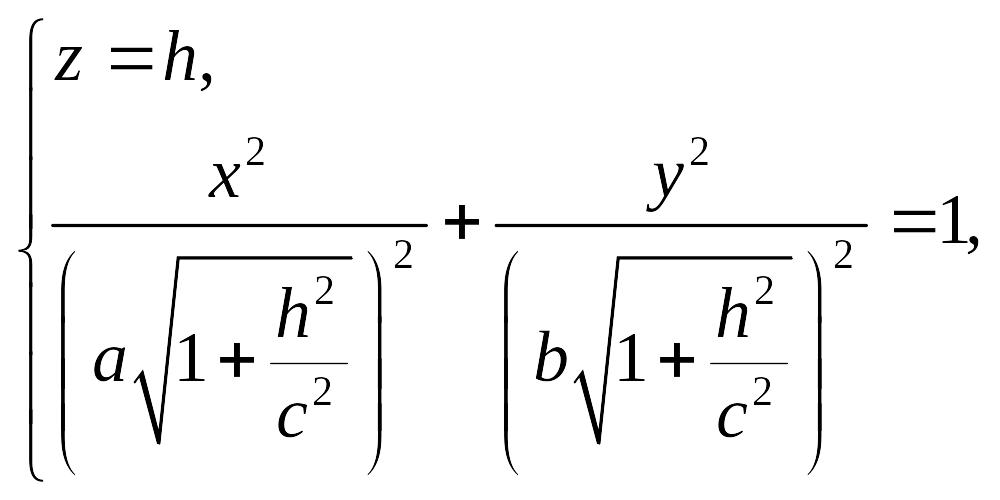 (18.5)
(18.5)
т.е
представляет собой эллипс с полуосями
![]() и
и
![]() Заметим, что полуоси неограниченно
увеличиваются с увеличением
Заметим, что полуоси неограниченно
увеличиваются с увеличением
![]() Таким образом, гиперболоид (18.4) представляет
собой поверхность, подобную трубке,
неограниченно расширяющейся в
положительном и отрицательном направлениях
по оси
Таким образом, гиперболоид (18.4) представляет
собой поверхность, подобную трубке,
неограниченно расширяющейся в
положительном и отрицательном направлениях
по оси
![]()
4. Линией пересечения однополостного гиперболоида с плоскостью будет гипебола
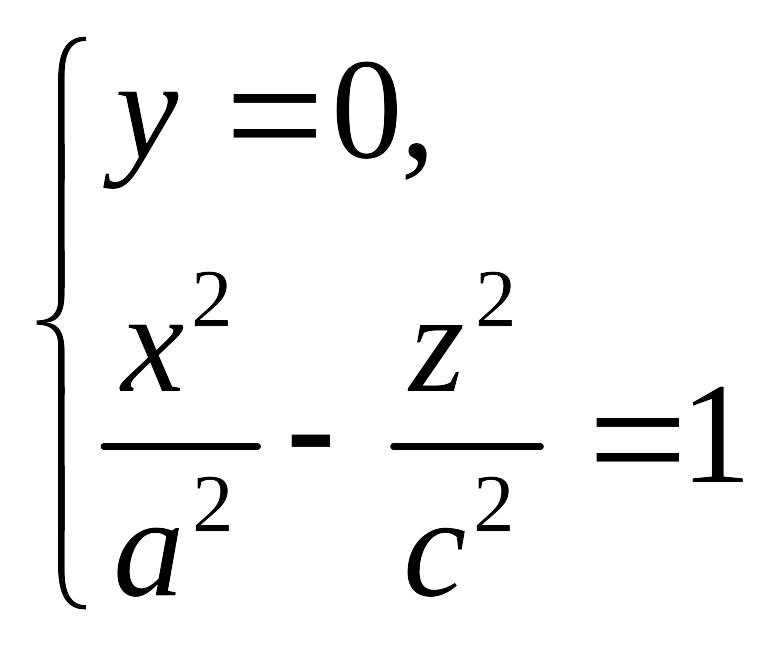
с действительной полуосью и мнимой полуосью А линией пересечения гиперболоида с плоскостью также является гипербола
с действительной полуосью и мнимой полуосью Таким образом, однополостной гиперболоид (18.4) имеет вид, изображенный на рис. 18.2. Def.
Если
линиями пересечения однополостного
гиперболоида (18.4) с плоскостями
|
Рис. 18.2 |
называется однополостным гиперболоидом вращения.
Def. Числа называют полуосями однополостного гиперболоида.
Двухполостной гиперболоид
Def. Двухполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
(18.6)
Исследуем форму двухполостного гиперболоида.
1. Из
уравнения (18.6) следует, что оси коодинат
являются осями симметрии двухполостного
гиперболоида, координатные плоскости
– плоскостями симметрии, а начало
отсчета – центром симметрии. Ось
поверхность пересекает в точках с
координатами
![]() точек пересечения с осями
и
нет.
точек пересечения с осями
и
нет.
2. В сечении двухполостного гиперболоида плоскостью имеем мнимый эллипс:
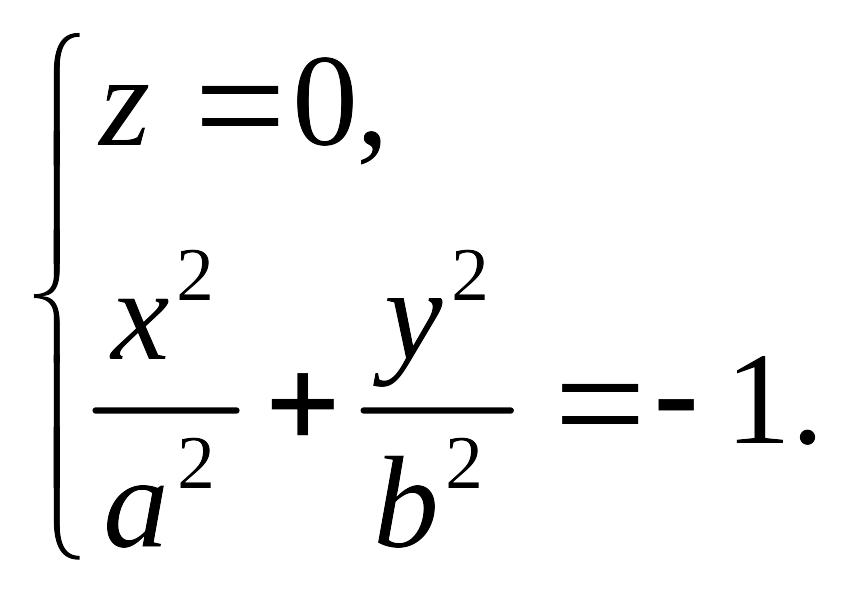
В сечении данного гиперболоида плоскостями получаем линию, задаваемую уравнением
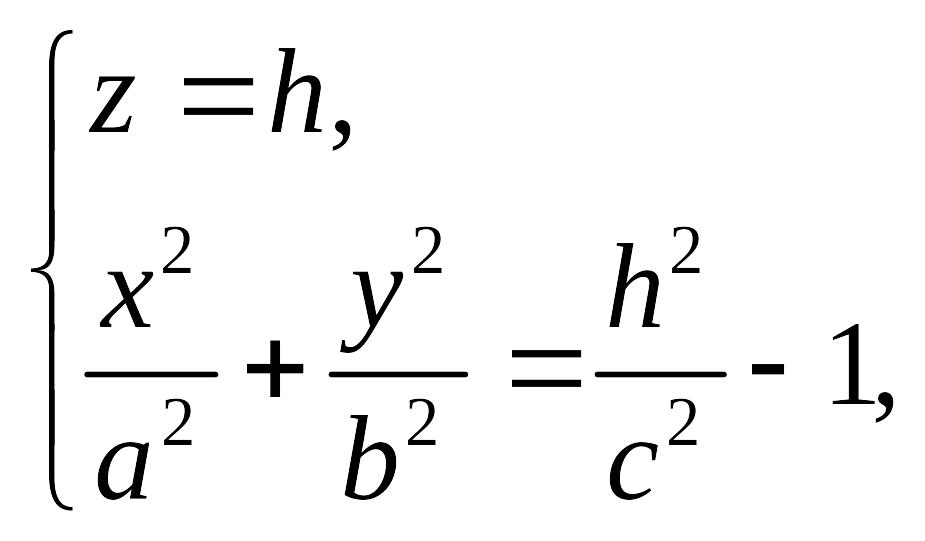
или
 (18.7)
(18.7)
Уравнение
(18.7) при
задает эллипс с полуосями
![]() и
и
![]() который при
вырождается в точку (точки пересечения
с осью
).
При
песечение двухполостного гиперболоида
(18.6) и плоскости
пусто.
который при
вырождается в точку (точки пересечения
с осью
).
При
песечение двухполостного гиперболоида
(18.6) и плоскости
пусто.
Это
значит, что в пространстве между
плоскостями
![]() не содержится точек рассматриваемой
поверхности, эта поверхность состоит
из двух полостей, расположенных так,
как показано на рис. 18.3.
не содержится точек рассматриваемой
поверхности, эта поверхность состоит
из двух полостей, расположенных так,
как показано на рис. 18.3.
3. Линия пересечения исследуемой поверхности и плоскости задается уравнением
Это
гипербола с действительной полуосью
Аналогично линией пересечения двухполостного гиперболоида и плоскости является гипербола
|
Рис. 18.3 |
с действительной полуосью и мнимой полуосью
Def. Числа называют полуосями двухполостного гиперболоида.
Def.
Если в гипербодоиде (18.6) в сечении
плоскостями
![]() получаются окружности, то его называют
двухполостным
гиперболоидом вращения.
получаются окружности, то его называют
двухполостным
гиперболоидом вращения.