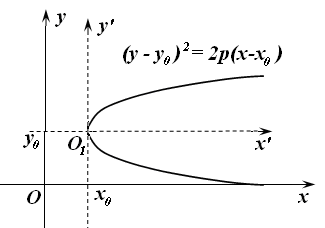- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
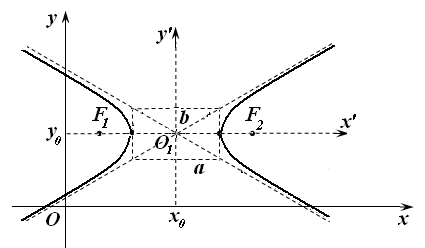
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Кривые второго порядка с осями симметрии параллельными координатным осям
Найдем
сначала уравнение эллипса с центром
в точке
|
Рис. 17.8 |
осям и и одинаково с ними направленными (рис. 17.8).
В этой системе координат уравнение эллипса имеет вид:
.
Но т.к.
![]() и
и
![]() (известные из школьного курса формулы
связи старых и новых координат при
параллельном переносе), то в старой
системе координат уравнение эллипса
имеет вид:
(известные из школьного курса формулы
связи старых и новых координат при
параллельном переносе), то в старой
системе координат уравнение эллипса
имеет вид:
![]() (17.4)
(17.4)
Рис. 17.9 |
Рассуждая
аналогично, получаем уравнение
гиперболы с центром в точке
действительной полуосью
и мнимой полуосью
|
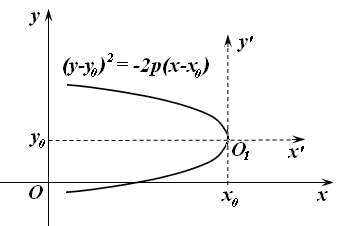
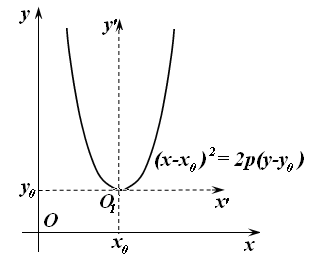
И, наконец, параболы, изображенные на рис. 17.8-17.11 имеют соответствующие уравнения:
Рис. 17.8
|
Рис. 17.9 |
Рис. 17.10 |
Рис. 17.11 |
![]()
Поверхности второго порядка
Def. Поверхностью второго порядка называется множество точек пространства, определяемое в некоторой прямоугольной декартовой системе координат уравнением второй степени:
![]()
![]() (18.1)
(18.1)
После применения движения и, возможно, умножения уравнения на ненулевой коэффициент, уравнение поверхности в трехмерном пространстве приводится к одному из следующих видов:
1.
![]() (эллипсоид)
(эллипсоид)
2.
![]() (мнимый эллипсоид)
(мнимый эллипсоид)
3.
![]() (однополостной гиперболоид)
(однополостной гиперболоид)
4.
![]() (двуполостной гиперболоид)
(двуполостной гиперболоид)
5.
![]() (конус)
(конус)
6.
![]() (мнимый конус)
(мнимый конус)
7.
![]() (эллиптический параболоид)
(эллиптический параболоид)
8.
![]() (гиперболический параболоид)
(гиперболический параболоид)
9. (эллиптический цилиндр)
10.
![]() (мнимый цилиндр)
(мнимый цилиндр)
11. (гиперболический цилиндр)
12. (параболический цилиндр)
13.
![]() (пара пересекающихся плоскостей)
(пара пересекающихся плоскостей)
14.
![]() (пара мнимых пересекающихся плоскостей)
(пара мнимых пересекающихся плоскостей)
15.
![]() (пара параллельных плоскостей)
(пара параллельных плоскостей)
16.
![]() (пара мнимых параллельны плоскостей)
(пара мнимых параллельны плоскостей)
17.
![]() (пара
совпадающих плоскостей)
(пара
совпадающих плоскостей)
Эллипсоид
Def. Эллипсоидом назывется поверхность, каноническое уравнение которой имеет вид:
(18.2)
Исследуем форму эллипсоида по его сечениям плоскостями.
1.
Очевидно, что эллипсоид пересекает оси
координат в точках
![]()
Из
уравнения (18.2) следует, что
![]() и
и
![]() т.е. эллипсоид представляет собой
поверхность, заключенную в параллелепипеде
т.е. эллипсоид представляет собой
поверхность, заключенную в параллелепипеде
![]() Координатные
плоскости являются плоскостями симметрии,
координатные оси – осями симметрии, а
начало координат – центром симметрии.
Координатные
плоскости являются плоскостями симметрии,
координатные оси – осями симметрии, а
начало координат – центром симметрии.
2.
Рассмотрим сечение данного эллипсоида
плоскостью
![]() Уравнение линии пересения имеет вид:
Уравнение линии пересения имеет вид:
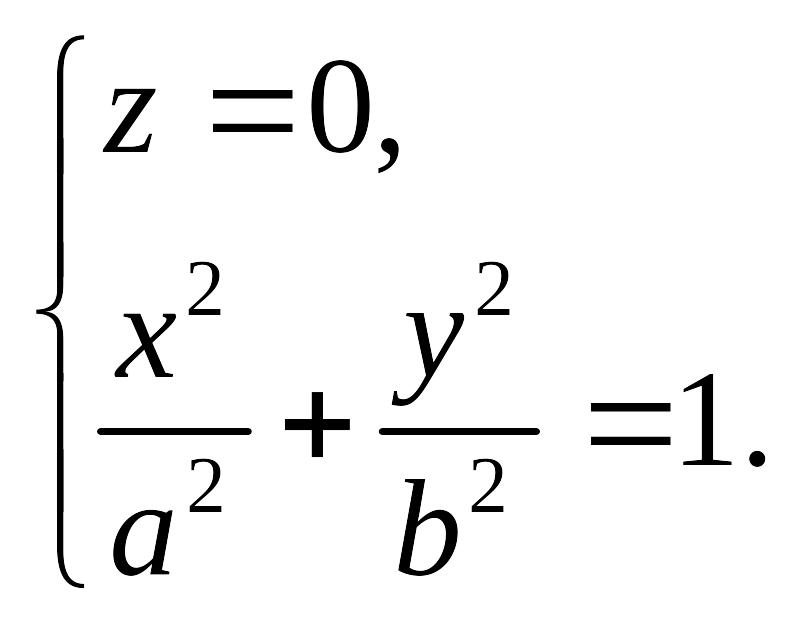
Данная линия представляет собой эллипс с полуосями и
Аналогично
устанавливаем, что пересечением
эллипсоида плоскостью
![]() будет эллипс
будет эллипс

с
полуосями
и
![]() а плоскостью
а плоскостью
![]() эллипс
эллипс

с
полуосями
и
![]()
3.
Рассмотрим теперь линию пересечения
эллипсоида с плоскостью
![]() параллельной плоскости
Уравнение этой линии имеет вид:
параллельной плоскости
Уравнение этой линии имеет вид:
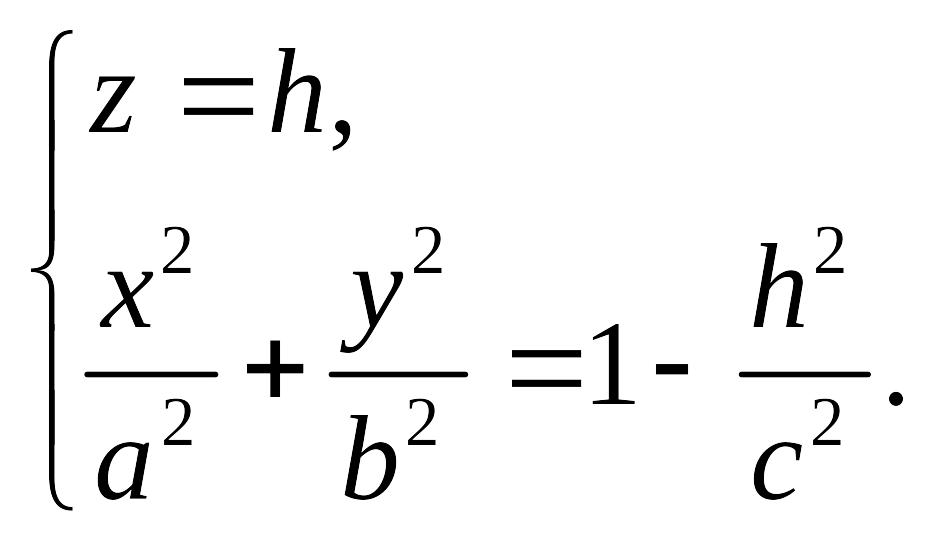
или
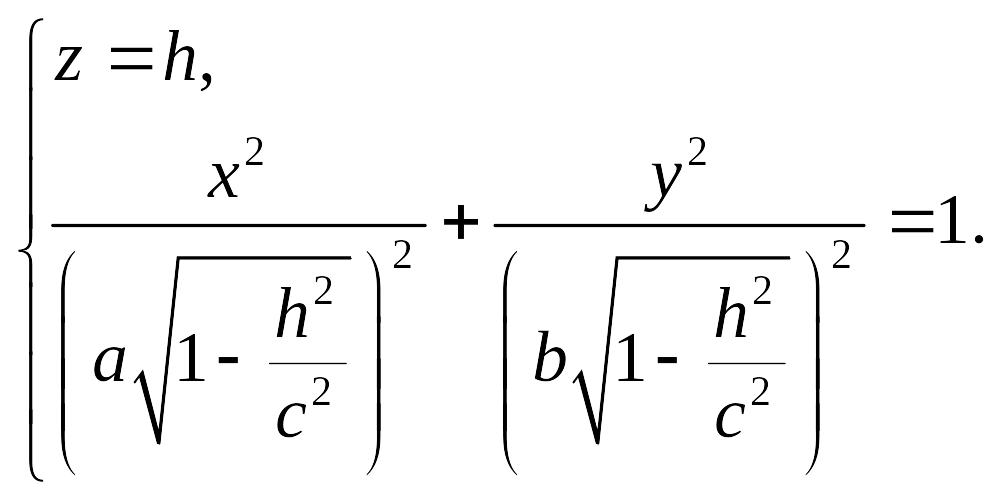 (18.3)
(18.3)
При
![]() уравнение (18.3) задает эллипс с полуосями
уравнение (18.3) задает эллипс с полуосями
![]() и
и
![]() При
При
![]() эллипсоид и эллипс не имеет общих точек.
При
эллипсоид и эллипс не имеет общих точек.
При
![]() эллипсоид и плоскость пересекаются в
одной точке (вырожденный эллипс).
эллипсоид и плоскость пересекаются в
одной точке (вырожденный эллипс).
Аналогично
находим, что в пересечении эллипсоида
с плоскостями
и
![]() также получаются эллипсы.
также получаются эллипсы.
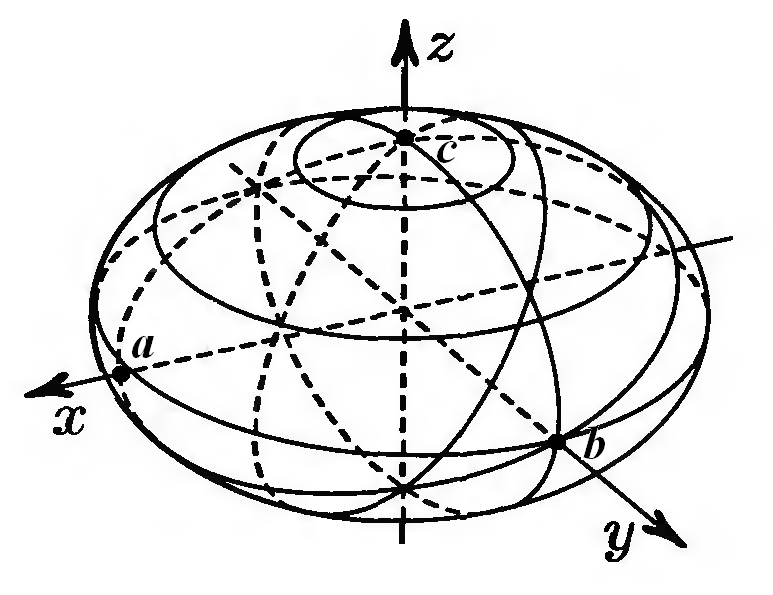
Таким образом, эллипсоид представляет собой ограниченную поверхность, линиями пересечения которой с координатными плоскостями и плоскостями, параллельными им, являются эллипсы (рис. 18.1). Def.
Числа
|
Рис. 18.1 |