
- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Геометрический смысл декартовой прямоугольной системы координат
Геометрический смысл декартовой прямоугольной системы координат выражается следующей теоремой.
Th.11.2 |
Если
|
Доказательство.
Пусть
С
другой стороны
|
Рис. 11.9 |
Но
![]() Теорема
доказана
.
Теорема
доказана
.
Следствие. Если то
![]() (11.5)
(11.5)
Доказательство вытекает из формулы длины диагонали в прямоугольном параллелепипеде.
Def.
Обозначим
углы, которые образует вектор
с координатными осями
через
соответственно.
![]() называются направляющими
косинусами
вектора
называются направляющими
косинусами
вектора
Из
треугольника
![]() (рис. 11.9):
(рис. 11.9):
![]() (11.6)
(11.6)
Аналогично получаем
![]() (11.7)
(11.7)
Нетрудно увидеть, что
![]() (11.8)
(11.8)
Скалярное произведение векторов
Def.
Скалярным
произведением
векторов называют число, равное
произведению их модулей на косинус угла
между ними. Обозначают
![]() или
или
![]() Т.е.
Т.е.
![]() (11.9)
(11.9)
где
угол между
и
![]()
Из формулы (11.9) имеем:
![]() (11.10)
(11.10)
Согласно
(11.2)
![]()
Заменяя
![]() по формуле (11.10), получаем:
по формуле (11.10), получаем:
![]() (11.11)
(11.11)
Соотношение (11.11) можно записать и в таком виде:
![]() (11.12)
(11.12)
Свойства скалярного произведения векторов
1.
2.
3.
4.
5.
Два ненулевых вектора
и
перпендикулярны тогда и только тогда,
когда
|
Доказательство.
Свойства 1, 2, 4, 5 вытекают непосредственно из определения. Докажем свойство 3. Согласно (11.12) и (11.4)
![]()
Что и требовалось доказать .
Th.11.3 |
Если
|
Доказательство.
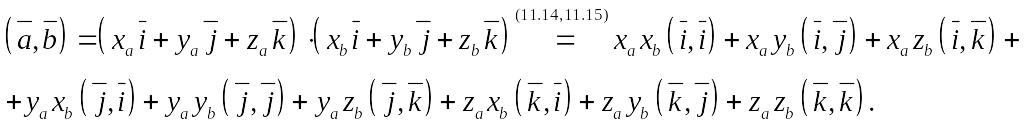 Согласно
(11.16)
Согласно
(11.16)
![]() А поскольку
взаимно перпендикулярные векторы, то
А поскольку
взаимно перпендикулярные векторы, то
![]()
Получаем
![]() .
.
N.
Векторы
и
образуют угол
![]() Найдите
Найдите
![]() если
если
![]() а
а
![]()
Решение.
Упростим
искомое выражение на основании свойств
скалярного произведения.
![]()
![]()
Согласно
свойству 4:
![]()
По определению скалярного произведения
![]()
Тогда,
![]()
Ответ.
![]()
![]()
Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
Def.
Векторным
произведением
векторов
и
называется
вектор
![]() определяемый следующим образом:
определяемый следующим образом:
1)
![]()
2) образуют правую тройку векторов;
3)
![]() где
угол между
и
где
угол между
и
Свойства векторного произведения
1.
2.
3.
4.
5.
6. Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение есть нулевой вектор. 7.
Модуль
векторного произведения
|
Доказательство.
1.
Очевидно, что векторы
и
![]() имеют
одинаковые модули, коллинеарны и
противоположно направлены, т.к. тройки
имеют
одинаковые модули, коллинеарны и
противоположно направлены, т.к. тройки
![]() и
и
![]() противоположной
ориентации (рис. 12.1). Значит,
противоположной
ориентации (рис. 12.1). Значит,
![]() .
.
2. Для утверждение очевидно, т.к. левая и правая часть соотношения (12.2) есть нулевой вектор.
Пусть
Также
|
Рис. 12.1 |
Учитывая,
угол между векторами
и
равен углу между векторами
и
![]() то
то
![]() Поэтому
Поэтому
![]()
![]() Аналогично свойство доказывается и для
Аналогично свойство доказывается и для
![]() .
.
3. Свойство 3 является непосредственным следствием свойств 1 и 2.
4. Для доказательства этого свойства воспользуемся следующей леммой.
Lemma |
Пусть
имеется два вектора
и
Обозначим
|
Доказательство леммы.
Векторы
и
|
Рис. 12.2 |
![]()
Выясним
направленность этих векторов. Вектор
лежит в плоскости
,
т.к
![]() Учитывая, что
Учитывая, что
![]() можем сделать вывод, что
можем сделать вывод, что
![]() (теорема о трех перпендикулярах). Значит,
и
коллинеарны. Кроме того, тройки
и
(теорема о трех перпендикулярах). Значит,
и
коллинеарны. Кроме того, тройки
и
![]() имеют одинаковую ориентацию. Значит,
и
сонаправлены. Откуда заключаем, что
имеют одинаковую ориентацию. Значит,
и
сонаправлены. Откуда заключаем, что
![]() .
.
Теперь
докажем свойство 4. Соотношение (12.4)
справедливо при
![]() Пусть
Пусть
![]() Обозначим
через
и
Обозначим
через
и
![]() проекции векторов
и
на
плоскость, перпендикулярную вектору
(рис. 12.3). Построим
проекции векторов
и
на
плоскость, перпендикулярную вектору
(рис. 12.3). Построим
![]() Тогда векторы
Тогда векторы
![]()
![]() и
и
![]() получаются из векторов
получаются из векторов
![]() и
и
![]() соответственно поворотом на угол
соответственно поворотом на угол
![]() И, следовательно,
И, следовательно,
![]()
А так как, согласно доказанной лемме,
![]()
то
![]() .
.
5. Свойство 5 является непосредственным следствием свойств 1 и 4.
6. Свойство 6 непосредственно вытекает из определения векторного произведения. 7.
Действительно,
|
|
Th.12.1 |
(выражение векторного произведения через координаты сомножителей) Если и то
|
Доказательство.
![]()
![]()
Согласно
свойству 6 векторного произведения
![]() По определению
По определению
![]()
Имеем
![]()
С другой стороны

Теорема доказана .
N.
Найти
площадь параллелограмма, построенного
на векторах
и
если
![]()
![]() где
где
![]()
Решение.
![]() Упростим
выражение
Упростим
выражение
![]() основываясь на свойствах векторного
произведения.
основываясь на свойствах векторного
произведения.
![]()
![]()
Вычислим
![]() ,
по формуле 12.6.
,
по формуле 12.6.
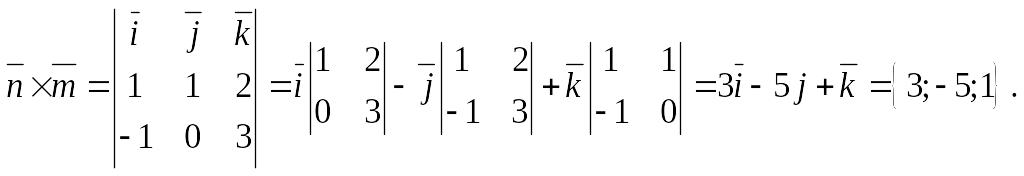
Значит,
![]()
Тогда
![]() (кв. ед.)
(кв. ед.)
Ответ.
![]() кв. ед.
кв. ед.


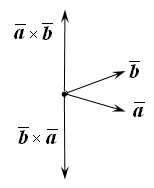
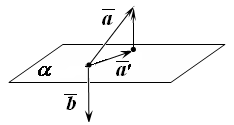
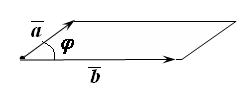 Рис.
12.3
Рис.
12.3 (12.6)
(12.6)