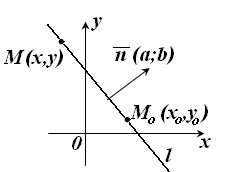- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
Def. Уравнением линии на плоскости в декартовой системе координат называют уравнение:
![]() ,
(13.1)
,
(13.1)
которому
удовлетворяют координаты
![]() любой точки этой линии и не удовлетворяют
координаты ни одной точки, которые не
принадлежат ей.
любой точки этой линии и не удовлетворяют
координаты ни одной точки, которые не
принадлежат ей.
N.
Например,
![]() –
уравнение прямой, проходящей через
начало координат и являющейся биссектрисой
І и ІІІ
координатных четвертей.
–
уравнение прямой, проходящей через
начало координат и являющейся биссектрисой
І и ІІІ
координатных четвертей.
![]() - уравнение
окружности с центром в точке
- уравнение
окружности с центром в точке
![]() и
радиусом
и
радиусом
![]()
Пусть
линия
![]() задана уравнением
,
а линия
задана уравнением
,
а линия
![]() - уравнением
- уравнением
![]() .
Точки
пересечения
этих линий, если они существуют,
принадлежат обеим линиям, т.е. удовлетворяют
обоим уравнениям. Таким образом, решение
задачи по отысканию точек пересечения
и
сводится к решению системы уравнений:
.
Точки
пересечения
этих линий, если они существуют,
принадлежат обеим линиям, т.е. удовлетворяют
обоим уравнениям. Таким образом, решение
задачи по отысканию точек пересечения
и
сводится к решению системы уравнений:
![]() (13.2)
(13.2)
N.
Найти точки пересечения окружности
![]() и прямой
и прямой
![]()
Решение.
Решим
систему уравнений
![]() Исключая из первого уравнения
Исключая из первого уравнения
![]() получаем:
получаем:
![]() Отсюда
Отсюда
![]() и, соответственно,
и, соответственно,
![]() .
Таким образом, точки
.
Таким образом, точки
![]() –
искомые.
–
искомые.
Def.
Алгебраической линией
называется такая линия, которая задается
в ДСК уравнением
,
где
![]() –
многочлен. Степень этого многочлена
называется порядком этой линии.
–
многочлен. Степень этого многочлена
называется порядком этой линии.
Def. Линии, которые не являются алгебраическими называются трансцендентными.
N.
![]() - алгебраическая линия второго порядка.
- алгебраическая линия второго порядка.
![]() – трансцендентные
линии.
– трансцендентные
линии.
Пусть заданы две функции одного аргумента:
![]() (13.3)
(13.3)
Условимся
рассматривать
![]() и
и
![]() как координаты некоторой точки
в заданной системе координат. Тогда при
изменении параметра
как координаты некоторой точки
в заданной системе координат. Тогда при
изменении параметра
![]() положение точки
меняется и она перемещается по плоскости.
Равенства (13.3) называются параметрическими
уравнениями
траектории точки.
положение точки
меняется и она перемещается по плоскости.
Равенства (13.3) называются параметрическими
уравнениями
траектории точки.
Пусть
уравнение (13.1) является следствием
(13.3), тогда ему удовлетворяют координаты
![]() любой точки
линии
(13.3) при любых
.
Если при этом, если точка
пробегает всю линию (13.1), то уравнение
представляет собой обычное уравнение
линии (13.3). Составление такого следствия
называют исключением параметра.
любой точки
линии
(13.3) при любых
.
Если при этом, если точка
пробегает всю линию (13.1), то уравнение
представляет собой обычное уравнение
линии (13.3). Составление такого следствия
называют исключением параметра.
N. Исключить параметр из параметрических уравнений траектории точки
![]()
Решение.
Возведем
каждое из уравнений в квадрат и сложим
их почленно. Получим:
![]() .
.
Значит,
точка
движется по окружности с центром в
начале координат и радиуса 1. Причем,
т.к.
![]() то луч
то луч
![]() образующий с осью
образующий с осью
![]() угол
угол
![]() занимает всевозможные положения. Значит,
точка М
пробегает указанную окружность
бесконечное число раз.
занимает всевозможные положения. Значит,
точка М
пробегает указанную окружность
бесконечное число раз.
Замечание. Не всегда возможно исключить параметр из параметрических уравнений линии.
Уравнение прямой на плоскости
Th. 13.1 |
Любая прямая на координатной плоскости может быть задана уравнением первой степени:
И, наоборот, любое уравнение первой степени определяет на плоскости прямую. |
|
Доказательство.
1)
Положение прямой
однозначно определяется точкой
Выберем
|
Рис. 13.1
|
|
Очевидно,
что
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() или
или
![]() В координатной форме последнее равенство
имеет вид:
В координатной форме последнее равенство
имеет вид:
![]() (13.5)
(13.5)
После
раскрытия скобок получаем
![]() ,
где
,
где
![]() Таким
образом, первая часть утверждения
теоремы доказана.
Таким
образом, первая часть утверждения
теоремы доказана.
2) Пусть
![]() –
одно из решений уравнения (13.4), т.е.
–
одно из решений уравнения (13.4), т.е.
![]() (13.6)
(13.6)
Вычтем
из уравнения (13.4) уравнение (13.6), получим
Это
уравнение является координатной записью
условия
![]() где
где
![]()
![]() Но это условие определяет прямую, которая
проходит через точку М
перпендикулярно вектору
Но это условие определяет прямую, которая
проходит через точку М
перпендикулярно вектору![]() .
Таким
образом, доказано и второе утверждение
теоремы
.
.
Таким
образом, доказано и второе утверждение
теоремы
.
Замечания.
1.
Уравнение
![]() называется уравнением
прямой, проходящей через точку
называется уравнением
прямой, проходящей через точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]()
2. Уравнение (13.4) называют общим уравнением прямой. Коэффициенты перед переменными в общем уравнении прямой на плоскости имеют вполне определенный геометрический смысл: они являются координатами нормального вектора прямой.
3.
Очевидно, что если в уравнении (13.4)
![]() то прямая проходит через начало координат.
то прямая проходит через начало координат.
4.
Если в уравнении (13.4)
![]() то
то
![]() В этом случае прямая параллельна оси
В этом случае прямая параллельна оси
![]() Аналогично, если в уравнении (13.4)
Аналогично, если в уравнении (13.4)
![]() то прямая параллельна оси
то прямая параллельна оси
![]()