Обратная матрица. Элементарные матрицы и их применение. Обратная матрица

Def. Матрица А^-1 называется обратной к матрице А, если А^-1А=А А^-1=Е.

Def. Матрица А называется невырожденной, если , в противном случае она называется вырожденной.

Th.6.1

Любая невырожденная матрица имеет обратную, которая находится по формуле: (6.1) где - алгебраические дополнения к элементам матрицы

Доказательство.

Докажем, что вырожденная матрица не имеет обратной.

Пусть и . Тогда с одной стороны , а с другой стороны . Противоречие. Значит, для вырожденной матрицы не существует обратной.

Проверим, что матрица заданная формулой (5.1) действительно является обратной к А. Для этого убедимся, что А^-1А=А А^-1=Е.

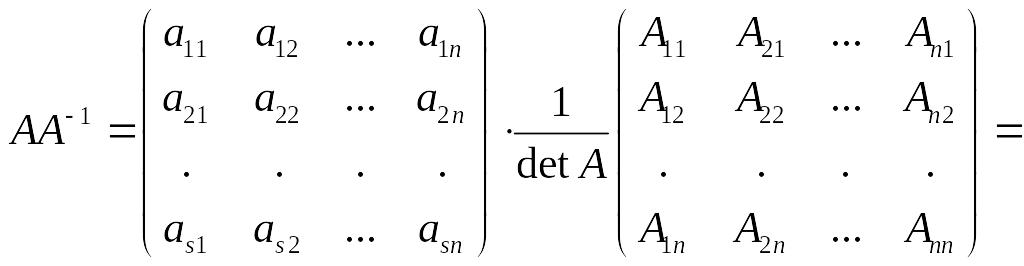
Найдем элемент матрицы В:

.

Если то и Если же то и Таким образом,

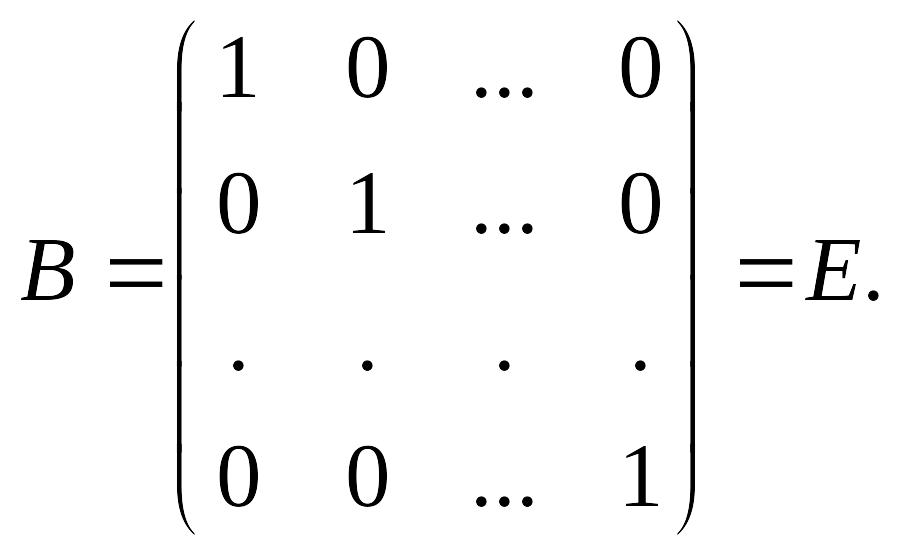
Аналогично доказываем, что

Свойства обратной матрицы:

. . .

Доказательство.

Свойство 1 вытекает непосредственно из определения.

Докажем свойство 2. По определению обратной матрицы .

. Поскольку то .

Докажем свойство 3.

.

.

По определению – обратная матрица для матрицы , т.е. .

Докажем свойство 4.

и Значит, по определению матрица – обратная матрица для , т.е.

Элементарные матрицы и их применение

Def. Элементарными преобразованиями строк (столбцов) матрицы называют любое из следующих действий:

1. перестановка любых двух строк (столбцов);

2. умножение любой строки (столбца) на некоторое число ;

3. прибавление к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число.

Пусть Т – элементарное преобразование строк (столбцов). Обозначим Т(А) – матрицу, которая получается из А с помощью этого преобразования.

Def. Всякая матрица Т(Е) называется элементарной матрицей.

Th.6.2

Если Т – некоторое элементарное преобразование строк то: Т(А)=Т(Е)·А

Доказательство.

Пусть Т – перестановка i –ой j – ой строк . Тогда:

Пусть Т – умножение i –ой строки на некоторое число . Тогда:

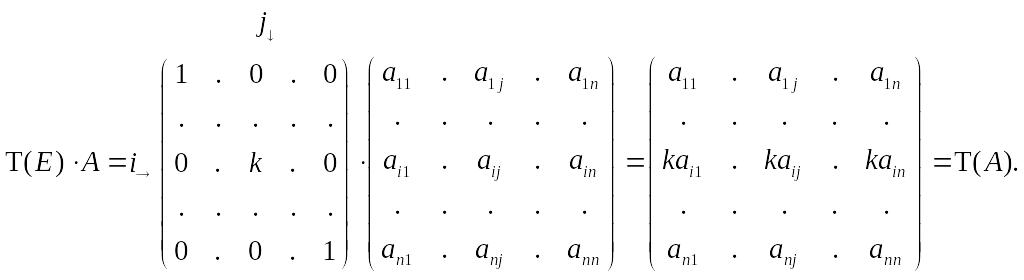Пусть Т – прибавление к i –ой строке j – ой строки, умноженной на некоторое число . Тогда:

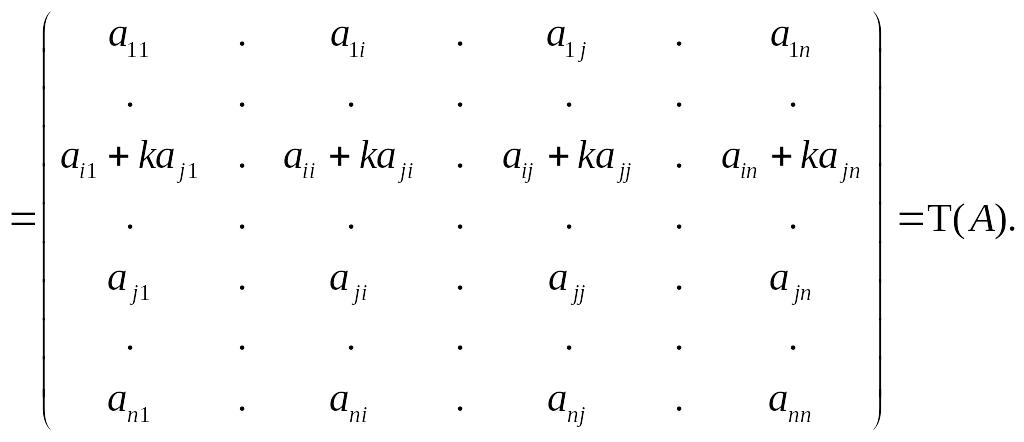
Th.6.3

Если Т – некоторое элементарное преобразование столбцов, то Т(А)= А ·Т(Е)

Доказательство.

Отличается от доказательства теоремы 6.3 только заменой строк на столбцы.

Таким образом, теоремы 6.2 и 6.3 утверждают, что всякое элементарное преобразование строк (столбцов) матрицы А равносильно умножению слева (справа) на соответствующую элементарную матрицу.

Метод Жордана-Гаусса нахождения обратной матрицы

Этот метод состоит в следующем: к матрице А справа приписывают единичную матрицу того же размера, затем элементарными преобразованиями одних только строк (!) приводят матрицу А к единичной. Матрица, которая окажется справа, и будет обратной матрицей.

Для обоснования этого метода применим элементарные матрицы. Каждое элементарное преобразование строк есть умножение матрицы А на соответствующую элементарную матрицу. Пусть Т – произведение всех элементарных матриц, отвечающих элементарным преобразованиям, производимым над матрицей А. После их выполнения получим:

. Но согласно описанному методу мы получаем матрицу . Значит, , откуда , а именно эта матрица стоит справа в результате преобразований.

N. Найти обратную матрицу к А с помощью метода Жордана-Гаусса.

.

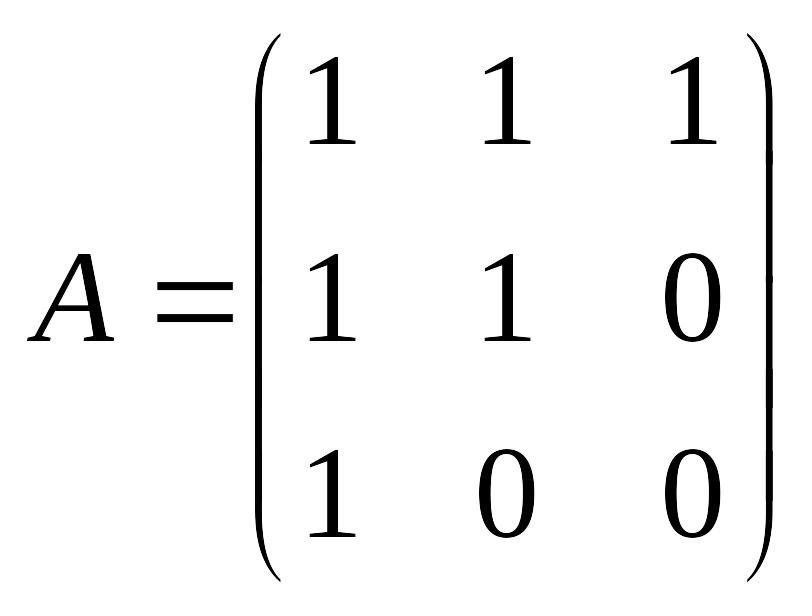Решение.

Припишем к матрице А справа единичную матрицу и с помощью элементарных преобразований строк получим слева единичную матрицу:

Жордан Камиль Мари Эдмон (5.1.1838 - 21.1.1922)-французский математик. Его работы относятся к алгебре, теории функций, топологии и кристаллографии. Написал первый систематический курс теории групп и теории Галуа (1870г.). Первый исследовал бесконечные группы.

.

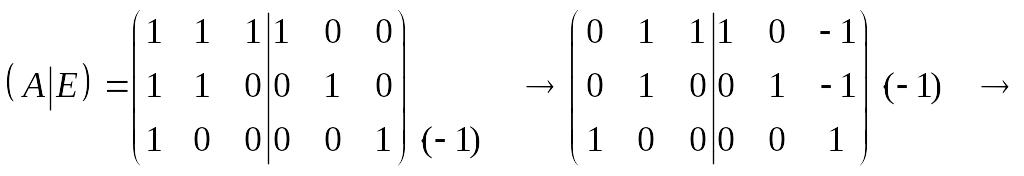
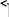
Значит, .