- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Эллиптический параболоид
Def. Эллиптическим параболоидом называется поверхность, каноническое уравнение которой имеет вид
![]() (18.8)
(18.8)
Исследуем форму эллиптического параболоида.
1. Из
уравнения (18.8) видно, что координатные
плоскости
и
являются плоскостями симметрии
эллиптического параболоида, а ось
– его осью симметрии. При
![]() эллиптический параболоид расположен
в полупространстве
эллиптический параболоид расположен
в полупространстве
![]() а при
а при
![]() – в полупространстве
– в полупространстве
![]()
2. Исследуем форму эллиптическогопараболоида при по его сечениям координатными плоскостями и параллельными им плоскостями. Уравнениями линии пересечения эллиптического параболоида с плоскостью будут
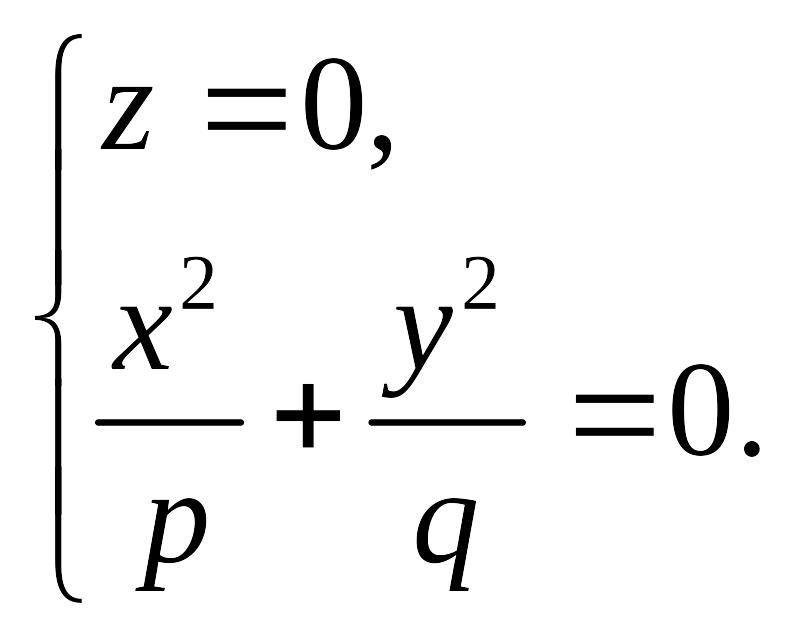
Это
уравнение определяет точку
![]() – начало координат.
– начало координат.
Уравнения
линий пересечения данного параболоида
с плоскостями
![]() параллельными координатной плоскости
параллельными координатной плоскости
![]() имеют вид
имеют вид
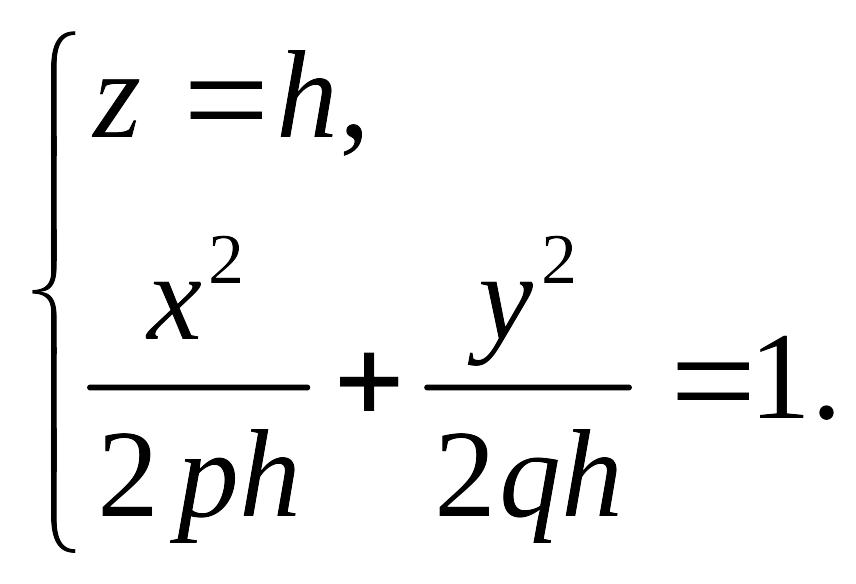 (18.9)
(18.9)
Это
эллипсы с полуосями
![]() и
и
![]() Причем при возрастании
Причем при возрастании
![]() полуоси эллипса неограниченно возрастают.
полуоси эллипса неограниченно возрастают.
3. Линией пересечения эллиптического параболоида (18.8) с плоскостью будет парабола
![]() (18.10)
(18.10)
Аналогично линией пересечения эллиптического параболоида (18.8) с плоскостью - парабола
![]() (18.11)
(18.11)
Плоскость
![]() пересекает данный параболоид по линии,
которая задается уравнением
пересекает данный параболоид по линии,
которая задается уравнением
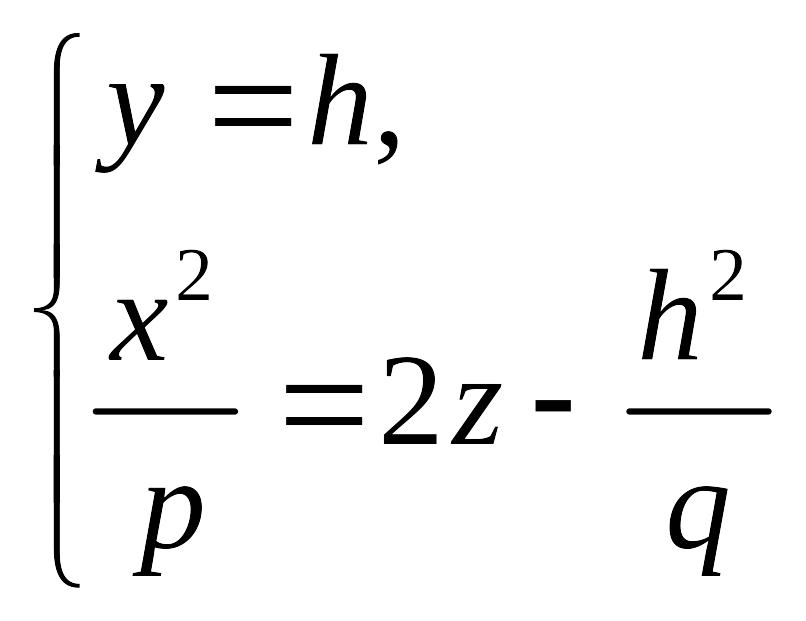
или
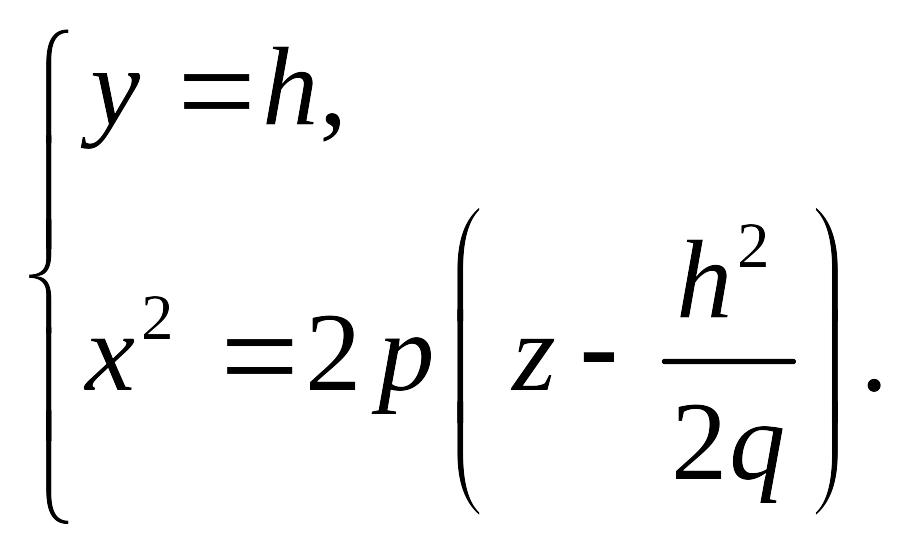 (18.12)
(18.12)
Уравнение
(18.12) задает параболу. Эта парабола
получается из параболы (18.10) с помощью
параллельного переноса, при котором
вершина параболы перемещается из точки
в точку
![]() Таким образом, эллиптический
параболоид (18.8) может быть образован
путем параллельного переноса параболы
(18.10), при котором ее вершина движется
по параболе (18.11).
Таким образом, эллиптический
параболоид (18.8) может быть образован
путем параллельного переноса параболы
(18.10), при котором ее вершина движется
по параболе (18.11).
Аналогичными
рассуждениями устанавливаем, что
плоскость
![]() пересекает эллиптический параболоид
по параболе
пересекает эллиптический параболоид
по параболе
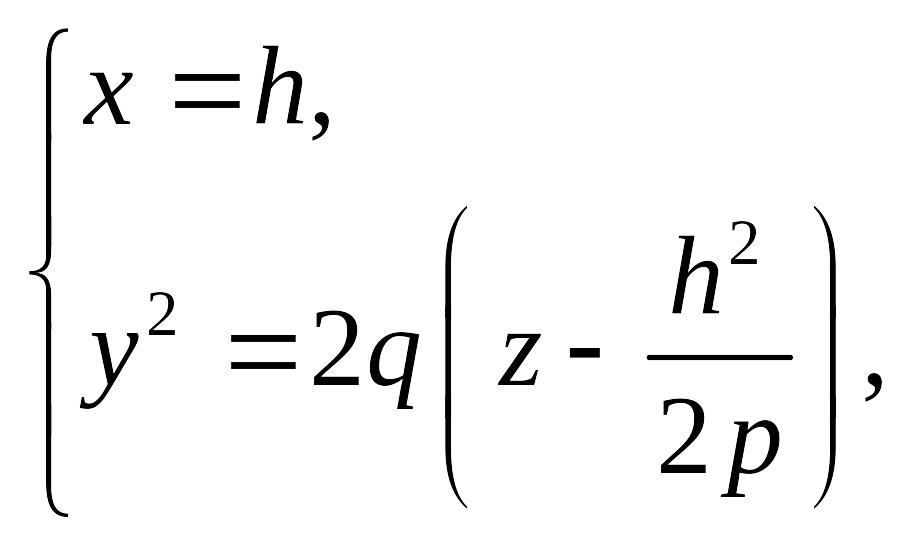
которая
представляет собой результат
параллельного переноса параболы
(18.11), при котором ее вершина перемещается
из точки
в точку
|
Рис. 18.4 |
Гиперболический параболоид
Def. Гиперболическим параболоидом называется поверхность, каноническое уравнение которой имеет вид
![]() (18.13)
(18.13)
Исследуем форму гиперболического параболоида.
1. Из уравнения (18.13) видно, что координатные плоскости и являются плоскостями симметрии гиперболического параболоида, а ось – его осью симметрии.
2. Исследуем форму эллиптическогопараболоида при по его сечениям координатными плоскостями и параллельными им плоскостями. Линией пересечения гиперболического параболоида с плоскостью будет парабола
![]() (18.14
(18.14
а с плоскостью - парабола
(18.15)
Плоскости
![]() пересекают гиперболический параболоид
по параболам
пересекают гиперболический параболоид
по параболам

или
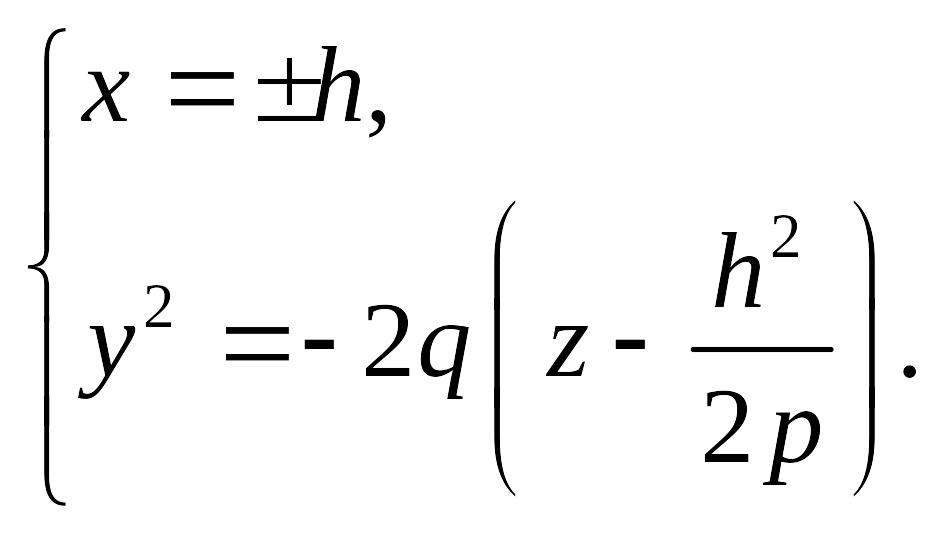 (18.16)
(18.16)
Эти
параболы представляют собой результат
паарллельного переноса параболы (18.15),
при котором ее вершина перемещается из
точки
в точки
![]() Т.е. гиперболический параболоид может
быть образован путем параллельного
переноса параболы (18.15), при котором ее
вершина движется по параболе (18.14).
Т.е. гиперболический параболоид может
быть образован путем параллельного
переноса параболы (18.15), при котором ее
вершина движется по параболе (18.14).
3. Линия пересечения гиперболического параболоида с плоскостью задается уравнением
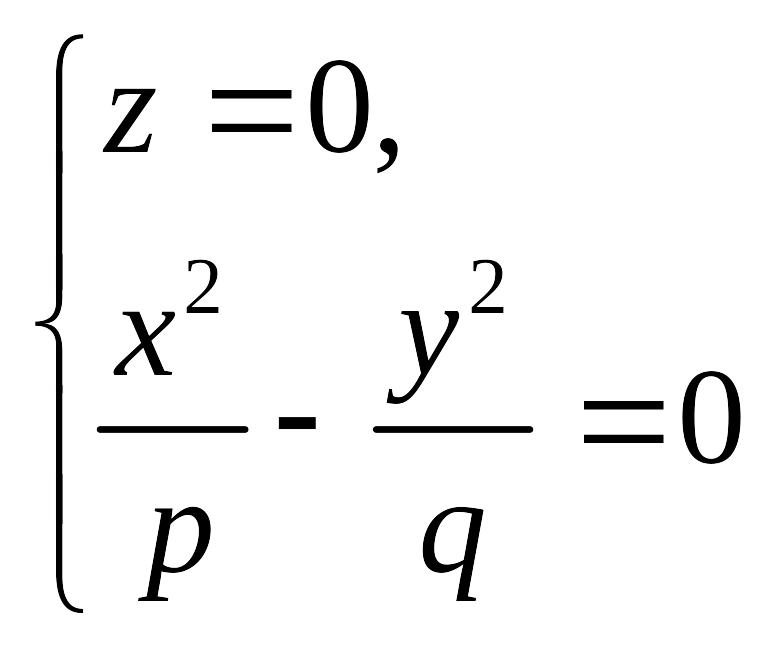
или
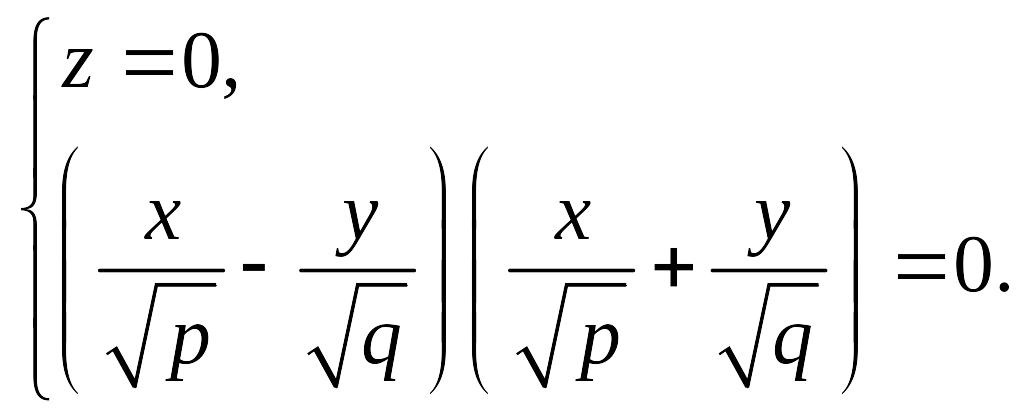 (18.17)
(18.17)
Уравнение (18.17) задает пару пересекающихся прямых.
Линии
персечения гиперболического параболоида
с плоскостями
представляют собой при
![]() гиперболу
гиперболу
с
действительной полуосью
и мнимой полуосью
|
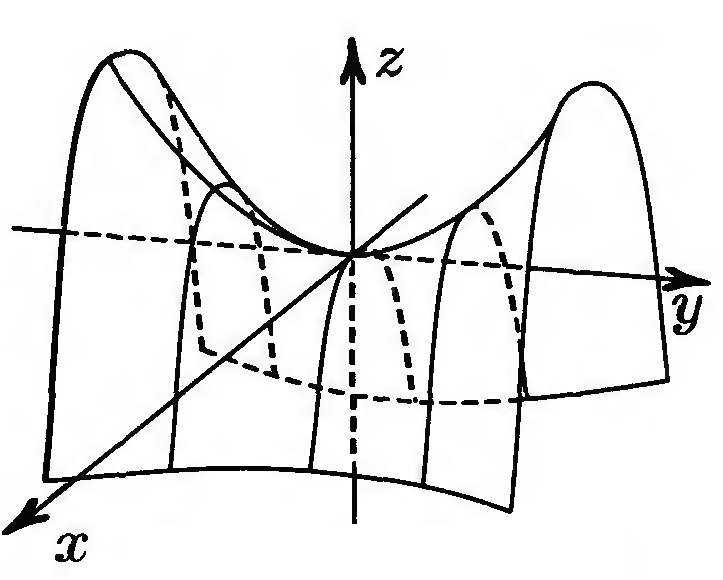
Рис. 18.5 |
с
действительной полуосью
![]() и мнимой полуосью
и мнимой полуосью
![]()
Гиперболический параболоид изображен на рис. 18.5.
Цилиндрические поверхности
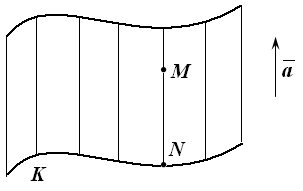
Def. Цилиндрической поверхностью (цилиндром) называется поверхность, образованная движением прямой, которая пересекает кривую и параллельна данному вектору (рис. 18.6). Def. Прямая, которая своим движением образует цилиндрическую поверхность называется образующей, а кривая – |
Рис. 18.6 |
направляющей цилиндра.
Th. 18.1 |
Если
образующая цилиндра параллельна оси
|
Доказательство.
Пусть
![]() – произвольная точка цилиндрической
поверхности и
ее направляющая в плоскости
с уравнением
.
Через точку
проведем образующую и обозначим через
– произвольная точка цилиндрической
поверхности и
ее направляющая в плоскости
с уравнением
.
Через точку
проведем образующую и обозначим через
![]() точку ее пересечения с направляющей
(рис. 18.6). Очевидно, что в плоскости
точка
имеет координаты
точку ее пересечения с направляющей
(рис. 18.6). Очевидно, что в плоскости
точка
имеет координаты
![]() и
и
![]() Тогда координаты точки
удовлетворяют уравнению
.
Тогда координаты точки
удовлетворяют уравнению
.
Следствия.
1.
Если образующая цилиндра параллельна
оси
то его уравнение имеет вид
![]() где
где
![]() – уравнение направляющей в плоскости
– уравнение направляющей в плоскости
![]()
2.
Если образующая цилиндра параллельна
оси
то его уравнение имеет вид
![]() где
где
![]() – уравнение направляющей в плоскости
– уравнение направляющей в плоскости
![]()
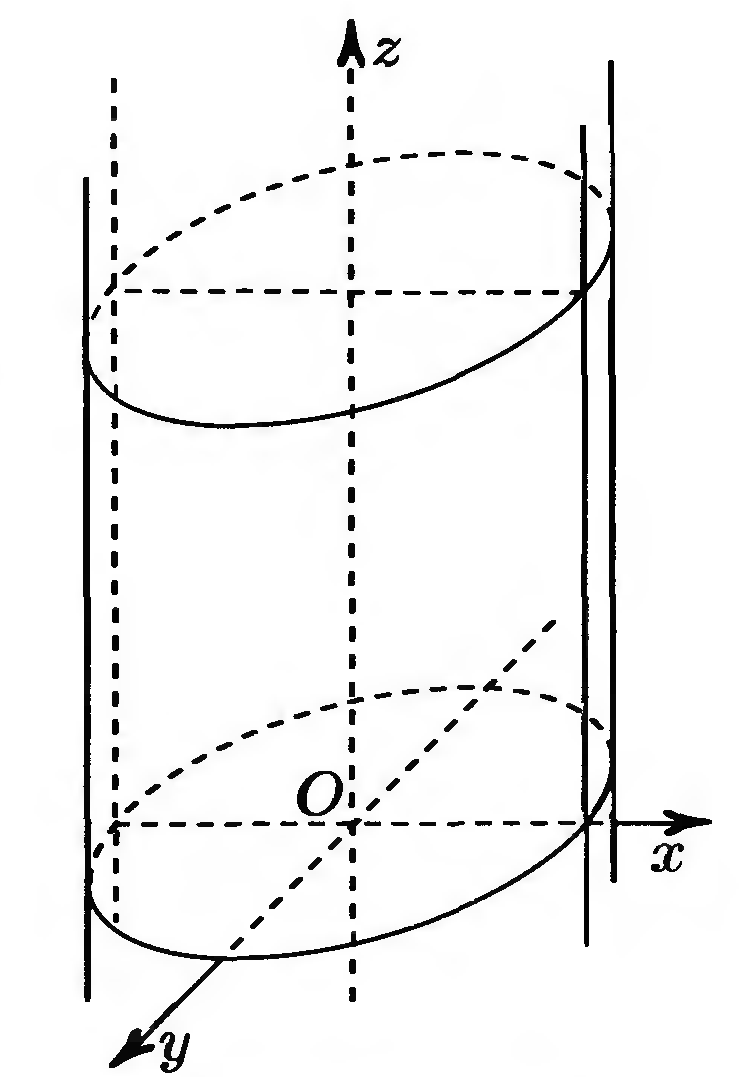
Def. Цилиндрами второго порядка называются цилиндрические поверхности, направляющие которых являются кривыми второго порядка.
Среди всех цилиндров второго порядка выделим те, обрающие которых параллельны оси Согласно теореме 18.1. их уравнения не содержат аппликаты. Их изображения приведены на рис. 18.7 – 18.9.
Эллиптический цилиндр
Рис. 18.7 |
Параболический цилиндр
Рис. 18.8 |
Гиперболический цилиндр
Рис. 18.9 |
|
Конические поверхности
Def.
Конической
поверхностью (конусом)
называется поверхность, образованная
прямыми, проходящими через данную
точку
Def. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением |
Рис. 18.10 |
![]() (18.18)
(18.18)
Покажем,
что если точка
![]() (отличная от начала координат) лежит на
конусе второго порядка, то все точки
прямой
(отличная от начала координат) лежит на
конусе второго порядка, то все точки
прямой
![]() (
(![]() – начало координат) также лежит на
конусе. Пусть
– начало координат) также лежит на
конусе. Пусть
![]()
![]() – направляющий вектор прямой
– направляющий вектор прямой
![]() Согласно (15.2) координаты произвольной
точки
Согласно (15.2) координаты произвольной
точки
![]() удовлетворяют соотношениям
удовлетворяют соотношениям
![]()
Очевидно, что координаты точки удовлетворяют уравнению (18.18), т.е. точка лежит на поверхности конуса. Что и требовалось доказать.
Исследуем форму эллипса по его сечениям координатными плоскостями и плоскостями параллельными им.
1. Линия
пересечения конуса второго порядка
плоскостью
![]() задается уравнением
задается уравнением
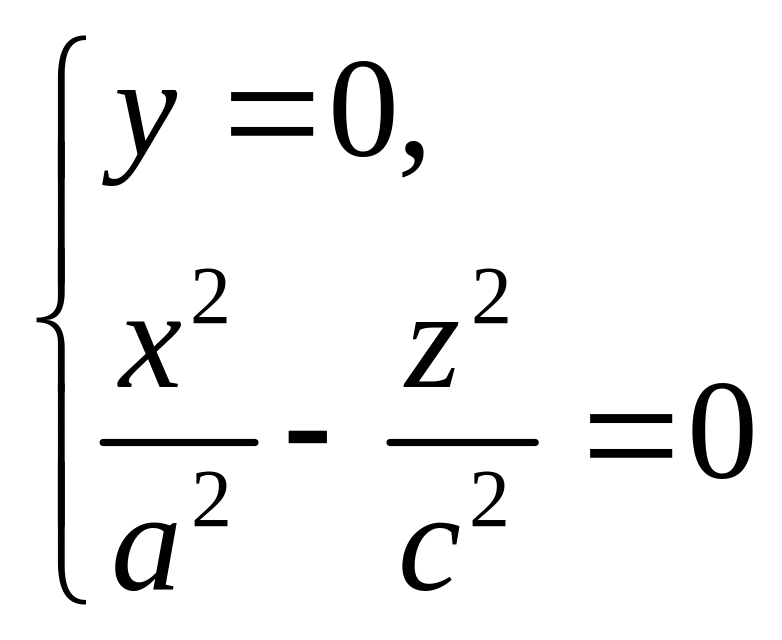 или
или
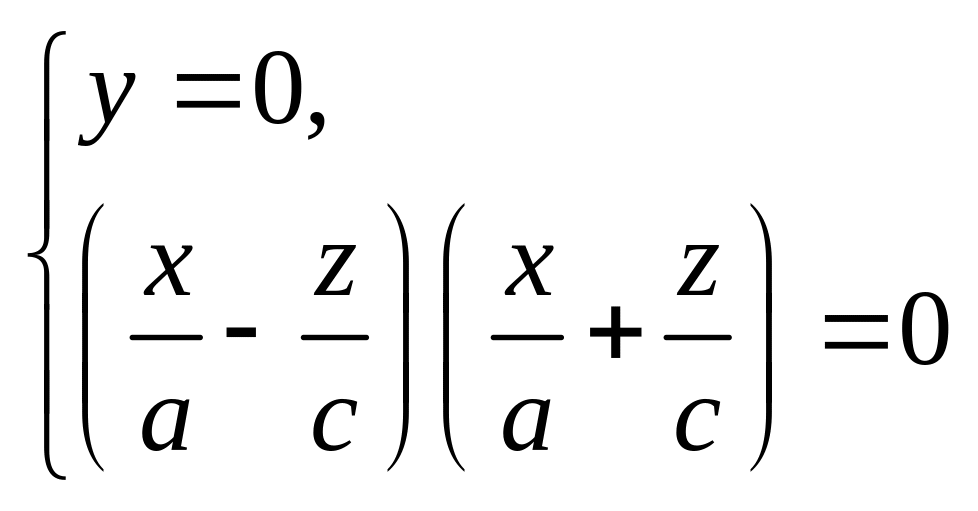 (18.19)
(18.19)
Уравнение (18.19) задает пару пересекающихся прямых.
Аналогично
можно установить, что плоскость
![]() пересекает конус второго порядка также
по двум пересекающимся прямым.
пересекает конус второго порядка также
по двум пересекающимся прямым.
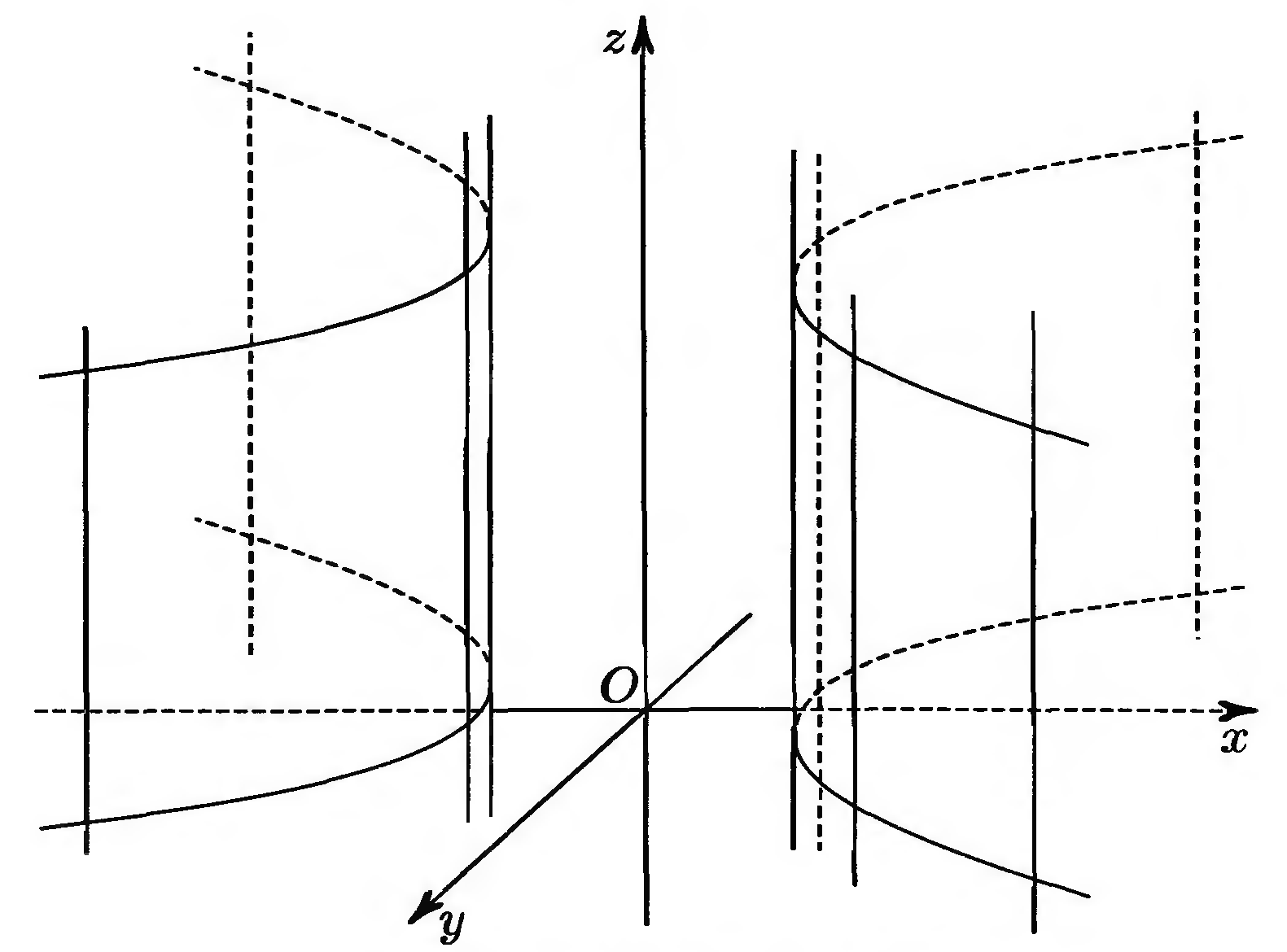
2.
Уравнения линий пересечения конуса
второго порядка с плоскостями
или
Уравнение
(18.20) задает эллипс с полуосями
|
Рис. 18.11 |
второго порядка представлено на рис. 18.11.
Def.
Если в уравнении (18.18)
![]() то сечения конуса второго порядка
плоскостями
– окружности. Такой конус называется
круглым.
то сечения конуса второго порядка
плоскостями
– окружности. Такой конус называется
круглым.


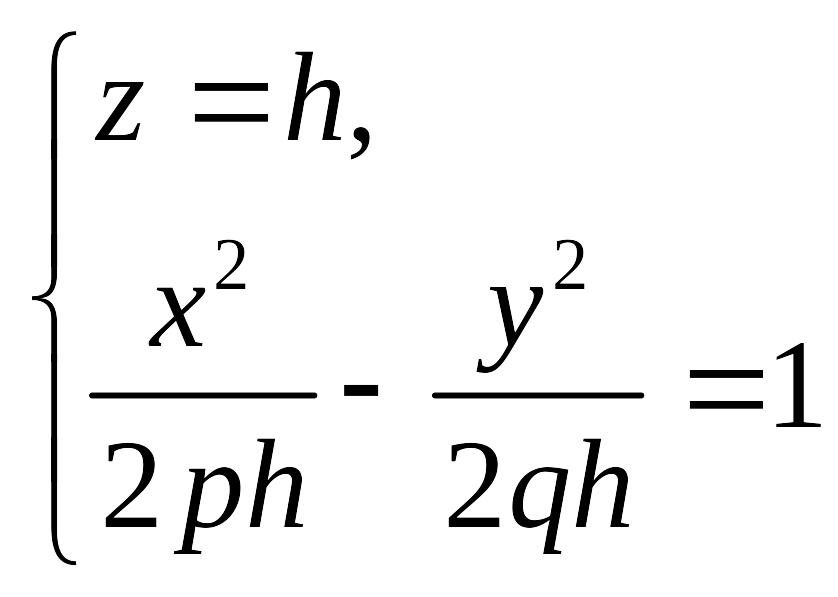
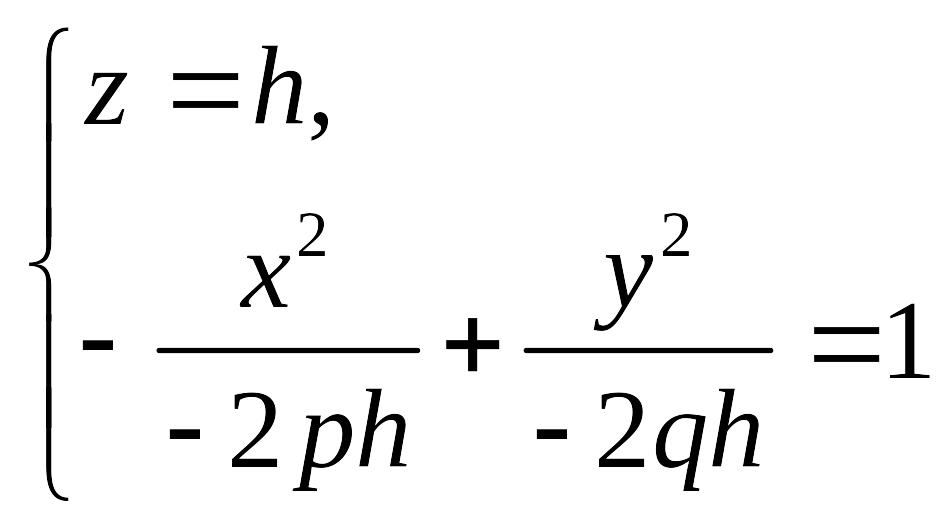



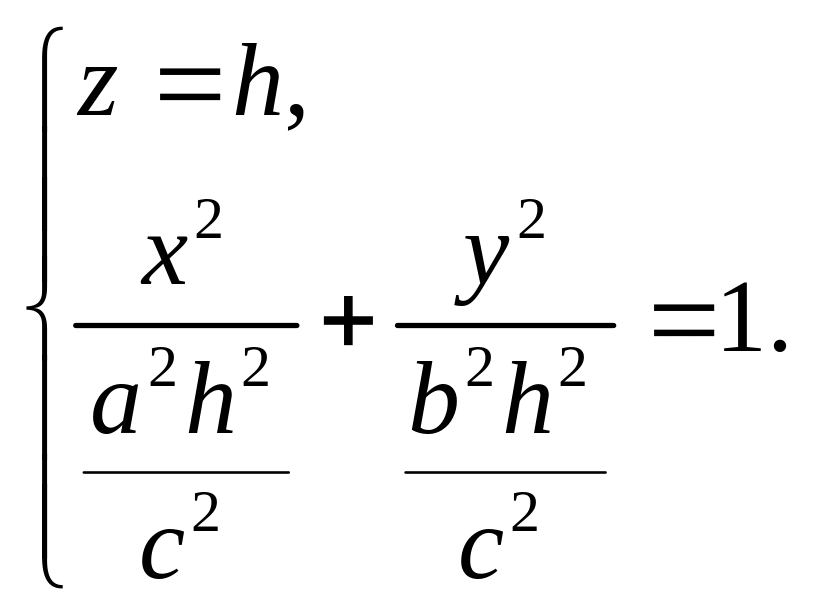 (18.20)
(18.20)