Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения

Def. Пусть дан определитель n-го порядка. Выберем в нем произвольные k строк и k столбцов ( ). Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель этой матрицы называют минором k-го порядка (М) определителя .

Def. Если вычеркнуть строки и столбцы, на пересечении которых находится минор М, то оставшиеся элементы образуют матрицу порядка n-k, определитель которой называется дополнительным минором к минору М и обозначается .

В частности, дополнительный минор к элементу обозначается .

Def. Пусть минор k-го порядка расположен в строках с номерами и в столбцах с номерами . Обозначим

Алгебраическим дополнением для минора М называют число .

В частности, алгебраическое дополнение к элементу обозначается и .

N . Пусть дан определитель .

– минор 2-го порядка, 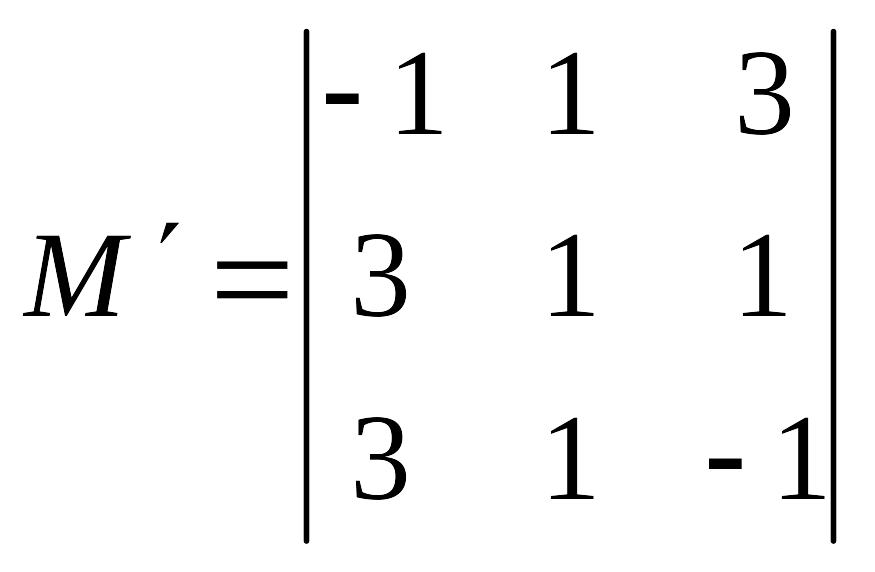– дополнительный минор к , 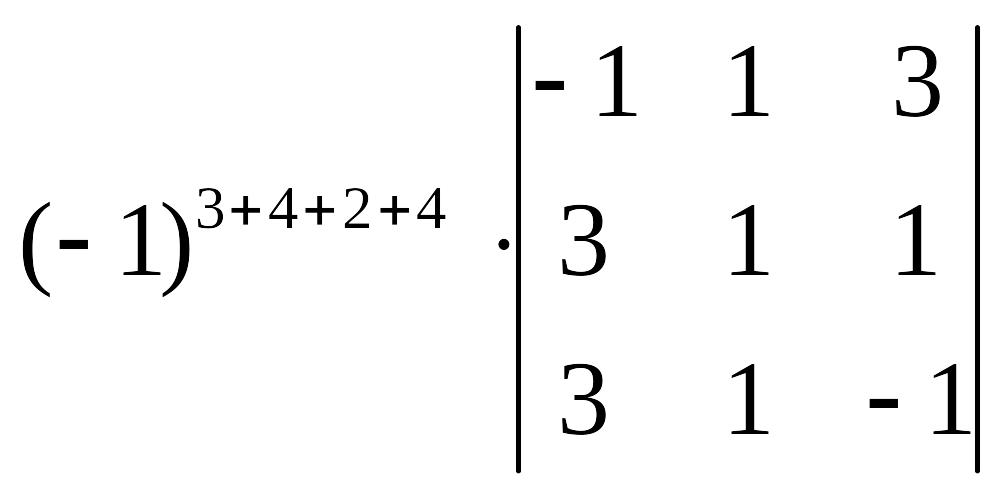– алгебраическое дополнение для .

Смысл алгебраического дополнения становится ясен из следующей леммы.

Lemma

Произведение любого минора определителя на его алгебраическое дополнение есть сумма, слагаемые которого являются некоторыми членами определителя

Доказательство.

1) Рассмотрим сначала случай, когда выбранный минор k-го порядка расположен в верхнем левом углу определителя.

Произвольный член минора М имеет вид , где l – число инверсий в перестановке . Произвольный член его дополнительного минора имеет вид , где t – число инверсий в перестановке .

Члены алгебраического дополнения будут получены из членов минора умножением на , т.е. будут равны членам дополнительного минора.

Произведение членов и имеют вид .

Элементы расположены в разных строках и разных столбцах определителя. Найдем знак, с которым входит произведение в определитель. Для этого определим число инверсий в перестановке . Все принимают значения от 1 до k, а принимают значения от k+1 до n, поэтому между собой и не будут образовывать инверсии и общее число инверсий равно l+t, т.е. слагаемые, входящие в произведение и равны членам определителя.

2) Рассмотрим общий случай. Пусть минор расположен в строках с номерами с номерами и в столбцах с номерами .

Переставляя строки и столбцы определителя, передвинем минор в верхний левый угол. Для этого строку поменяем местами со всеми предыдущими, передвинув на первое место, т.е. выполним транспозицию.

Для того, чтобы строка заняла второе место, подвергнем ее транспозиции и т.д., строку подвергнем транспозициям. Всего транспозиций строк: . В результате минор М будет расположен в первых k строках.

Далее последовательно переставляем столбцы: , пока он не займет первое место, , пока он не займет второе место и т.д. Имеем всего транспозиций столбцов. Полученный определитель отличается от исходного множителем . Согласно доказанному в первом случае, произведение состоит из слагаемых, входящих в состав определителя.

Th.4.1

(теорема Лапласа) Сумма произведений всех миноров k-го порядка, расположенных в выбранных строках, на соответствующие им алгебраические дополнения равно определителю.

Доказательство.

– суммa нескольких слагаемых определителя. Пересчитаем число всех таких слагаемых в произведении всех миноров k-го порядка, расположенных в выбранных строках.

Число слагаемых в миноре k-го порядка равно , число слагаемых в его алгебраическом дополнении . Тогда содержит слагаемых.

Количество миноров k-го порядка в выбранных строках равно . Значит, сумма произведений всех миноров k-го порядка, расположенных в выбранных строках, на их алгебраические дополнения содержит слагаемых, т.е. равна соответствующему определителю.

Теоремы 4.2 и 4.3 являются следствиями теоремы Лапласа.

Th.4.2

(разложение определителя по строке или столбцу) Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т.е. (4.1) или (4.2)

Формула 4.1 называется разложением определителя по элементам строки, а формула 4.2 – разложением определителя по элементам столбца.

Th.4.3.

(Определитель с углом нулей) П усть , где B – матрица размера и D – матрица размера . тогда .

Доказательство.

Для доказательства достаточно разложить определитель по теореме Лапласа, выбирая миноры n-го порядка в первых n строках.