Метод Гаусса
Рассмотрим
СЛУ (1.1). Не нарушая общности, можем
считать, что
.
Преобразуем эту СЛУ так, чтобы исключить
неизвестное
из всех уравнений кроме первого. Для
этого умножим первое уравнение на
и прибавим ко i
– му уравнению
.
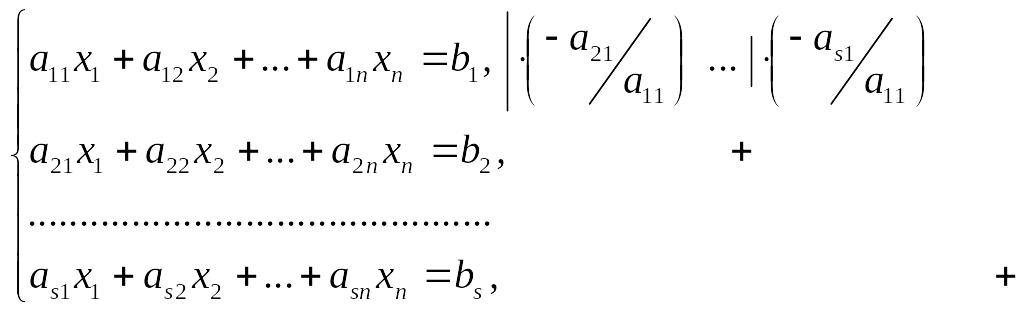
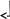
Приходим
к эквивалентной СЛУ, в которой s
уравнений и n
неизвестных (новые коэффициенты при
неизвестных –
,
новые свободные члены –
):
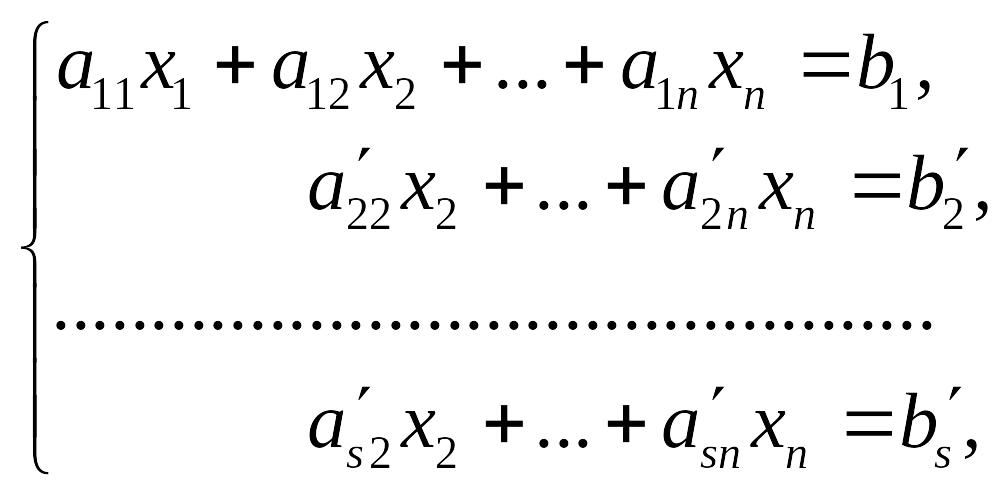(1.5)
Если в
СЛУ (1.5) есть уравнение, все коэффициенты
левой части которого равны нулю, а
свободный член отличен от нуля, то это
уравнение не удовлетворяется ни при
каких значениях переменных. Поэтому
можем сделать вывод о несовместности
системы. Если же в СЛУ (1.5) есть уравнение,
в котором и все коэффициенты левой части
и свободный член равны нулю, то очевидно
это уравнение удовлетворяется при любых
значениях неизвестных, поэтому, отбросив
его, мы приходим к равносильной системе.
Аналогично, избавляемся от переменной
во всех уравнениях кроме первого и
второго, затем
из всех уравнений кроме первых трех и
т.д. В результате таких преобразований
система (1.1) приведется к ступенчатому
виду:
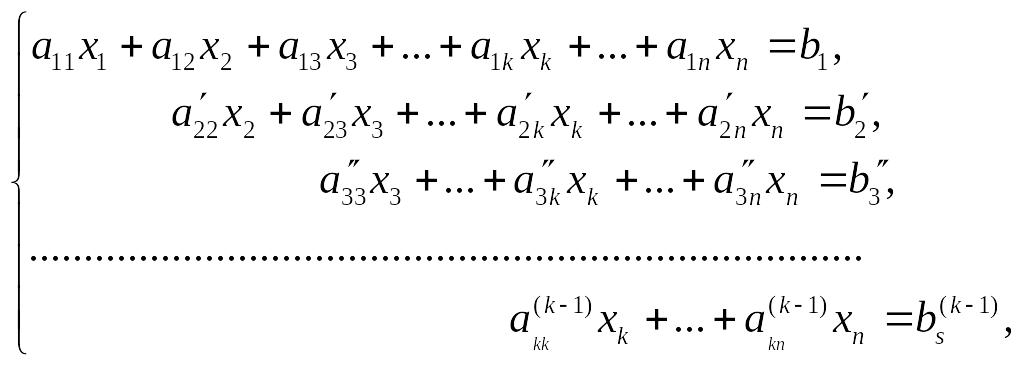(1.6)
Эта
часть решения СЛУ называется «прямым
ходом». Здесь
.
Очевидно, что
и
.
Дальнейшая часть решения (непосредственное
нахождение неизвестных) носит название
«обратного хода». Рассмотрим возможные
случаи.
1)
Если в
СЛУ (1.6)
,
то СЛУ сведется к «треугольному» виду:
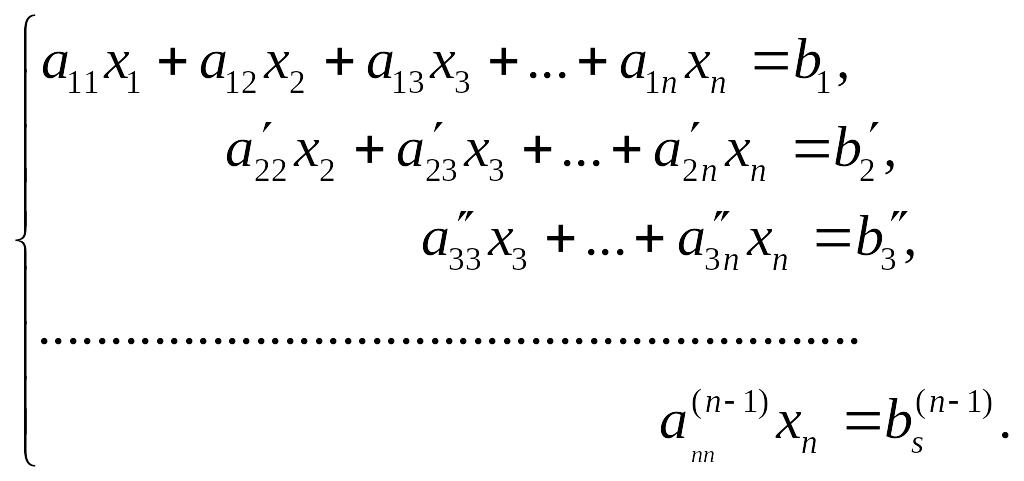(1.7)
Из
последнего уравнения СЛУ (1.7) найдем
.
Подставляя его в предпоследнее уравнение,
найдем
.
Продолжая аналогичным образом, получим,
что СЛУ (1.7), а значит и СЛУ (1.1), имеет
единственное решение.
2) Если
в СЛУ (1.6)
,
то система сводится к трапецеидальному
виду. В этом случае считаем переменные
«свободными». Придавая им произвольные
значения, найдем из последнего уравнения
,
после чего, двигаясь по системе снизу
вверх, как и выше, найдем значения
.
Так как значения для «свободных»
переменных можно выбрать бесконечным
числом способов, то система (1.7), а значит
и система (1.1) имеет бесконечное число
решений, т.е. неопределенная.
Таким образом, метод Гаусса применим для решения любой СЛУ. При этом, если в процессе преобразований получаем уравнение, у которого все коэффициенты левой части равны нулю, а свободный член не равен нулю, то СЛУ несовместна. В противном случае СЛУ совместна.
Если совместная СЛУ приводится к треугольному виду, то она будет определенной, а если к трапецеидальному - то неопределенной.
Отдельно
стоит остановиться на однородных СЛУ.
Такая система всегда совместна, поскольку
имеет тривиальное решение
.
Если однородной СЛУ число неизвестных больше числа уравнений, то она не может свестись к треугольному виду, поскольку в процессе «прямого хода» метода Гаусса число уравнений может лишь уменьшиться и не может увеличиться. Значит, однородная СЛУ в этом случае будет неопределенной.
При практическом решении СЛУ все преобразования проводят над строками расширенной матрицы системы.
|
Гаусс (Gauss) Карл Фридрих (30.04.1777 – 23.02.1855), немецкий математик, внёсший фундаментальный вклад также в астрономию и геодезию. Работы Гаусса оказали большое влияние на развитие высшей алгебры, теории чисел, дифференциальной геометрии, теории притяжения, классической теории электричества и магнетизма, геодезии, целых отраслей теоретической астрономии. |
