
- •И.Н. Реутова конспект лекций по алгебре и геометрии
- •Часть 1.
- •Содержание
- •Системы линейных уравнений и их матрицы. Сведение системы линейных уравнений к ступенчатому виду (метод гаусса) Системы линейных уравнений и их матрицы.
- •Метод Гаусса
- •Перестановки и подстановки. Определитель n-го порядка
- •Перестановки
- •Подстановки
- •Определитель n-го порядка
- •Свойства определителей. Свойства определителей
- •Миноры и алгебраические дополнения. Вычисление определителей. Правило крамера. Миноры и алгебраические дополнения
- •Вычисление определителей
- •1.Метод Гаусса.
- •2. На основании теоремы Лапласа.
- •3. Метод рекуррентных (возвратных) соотношений.
- •Правило Крамера.
- •Матрицы. Операции над матрицами. Линейные преобразования и матрицы
- •Линейные операции над матрицами
- •Нелинейные операции над матрицами
- •Обратная матрица. Элементарные матрицы и их применение. Обратная матрица
- •Элементарные матрицы и их применение
- •Метод Жордана-Гаусса нахождения обратной матрицы
- •Векторное n-мерное пространство. Линейная зависимость векторов. Ранг матрицы. Общая теория систем линейных уравнений. Векторное n-мерное пространство
- •Линейная зависимость векторов
- •Ранг матрицы
- •Системы линейных уравнений
- •Системы линейных однородных уравнений
- •Некоторые общие понятия алгебры. Поле комплексных чисел. Геометрическая интерпретация комплексных чисел. Группы. Кольца. Поля
- •Поле комплексных чисел
- •Алгебраическая форма записи комплексных чисел
- •Геометрическая интерпретация комплексных чисел
- •Извлечение корня n-ой степени из комплексного числа
- •Основные понятия векторной алгебры. Линейные операции над векторами и их свойства. Линейно зависимые (независимые) системы векторов. Базис. Координаты вектора. Основные понятия векторной алгебры
- •Линейные операции над векторами и их свойства
- •Линейная зависимость (независимость) векторов. Базис, координаты вектора
- •Декартова система координат. Координаты вектора
- •Проекция вектора на ось. Геометрический смысл декартовой системы координат. Скалярное произведение векторов. Проекция вектора на ось
- •Геометрический смысл декартовой прямоугольной системы координат
- •Скалярное произведение векторов
- •Векторное, смешанное и двойное векторное произведение векторов Векторное произведение векторов
- •Смешанное произведение векторов
- •Двойное векторное произведение векторов
- •Понятие об уравнении линии. Прямая на плоскости. Понятие об уравнении линии
- •Уравнение прямой на плоскости
- •Уравнение прямой с угловым коэффициентом
- •Другие виды уравнения прямой на плоскости
- •Взаимное расположение прямых на плоскости
- •Расстояние от точки до прямой
- •Уравнение пучка прямых
- •Плоскость в пространстве Уравнение плоскости в пространстве
- •Взаимное расположение плоскостей в пространстве.
- •Расстояние от точки до плоскости
- •Пучок плоскостей
- •Прямая в пространстве. Взаимное расположение прямой и плоскости в пространстве
- •Основные задачи на прямую в пространстве
- •1. Угол между двумя прямыми в пространстве.
- •3. Расстояние от точки до прямой в пространстве.
- •5. Расстояние между двумя скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве
- •1. Пересечение прямой и плоскости.
- •Кривые второго порядка
- •Гипербола
- •Кривые второго порядка (продолжение) Директрисы эллипса и гиперболы
- •Парабола
- •Кривые второго порядка с осями симметрии параллельными координатным осям
- •Поверхности второго порядка
- •Эллипсоид
- •Однополостной гиперболоид
- •Двухполостной гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Прямолинейные образующие поверхностей второго порядка
- •Рекомендованная литература
Плоскость в пространстве Уравнение плоскости в пространстве
Уравнению
первой степени
![]() на координатной плоскости соответствует
в координатном простанстве уравнение
на координатной плоскости соответствует
в координатном простанстве уравнение
![]() (14.1)
(14.1)
Th. 14.1 |
Каждое уравнение вида (14.1) определяет в пространстве плоскость наоборот, любая плоскость в координатном пространстве может быть задана уравнением (14.1) |
Доказательство этой теоремы полностью моделирует доказательство соответсвующего утверждения для прямой на плоскости (проведите его самостоятельно, используя рис. 14.1).
Рис. 14.1 |
Рис. 14.2
|
Уравнение
(14.1) называется общим уравнением
плоскости, вектор
![]() –
нормальным вектором плоскости.
–
нормальным вектором плоскости.
Если
плоскость проходит через точку
![]() перпендикулярно вектору
(рис. 14.1), то ее уравнение можно записать
в виде:
перпендикулярно вектору
(рис. 14.1), то ее уравнение можно записать
в виде:
![]() (14.2)
(14.2)
Плоскость
однозначно определяется точкой
![]() и двумя векторами
и двумя векторами
![]() и
и
![]() (
(![]() неколлинеарны). Векторы
и
называются направляющими
векторами плоскости.
Пусть
неколлинеарны). Векторы
и
называются направляющими
векторами плоскости.
Пусть
![]() –
текущая точка плоскости
–
текущая точка плоскости
![]() радиус вектор точки
радиус вектор точки
![]() радиус-вектор точки
(рис. 14.2).
радиус-вектор точки
(рис. 14.2).
![]() тогда и только тогда, когда векторы
тогда и только тогда, когда векторы
![]() компланарны. А поскольку
неколлинеарны,
то
компланарны. А поскольку
неколлинеарны,
то
![]() можно
разложить по этим векторам, т.е. имеет
место равенство:
можно
разложить по этим векторам, т.е. имеет
место равенство:
![]()
Учитывая,
что
![]() получаем:
получаем:
![]() (14.3)
(14.3)
Уравнение (14.3) называется векторным уравнением плоскости.
Т.к.
![]() тоуравнение (14.3) в координатной форме
принимает вид:
тоуравнение (14.3) в координатной форме
принимает вид:
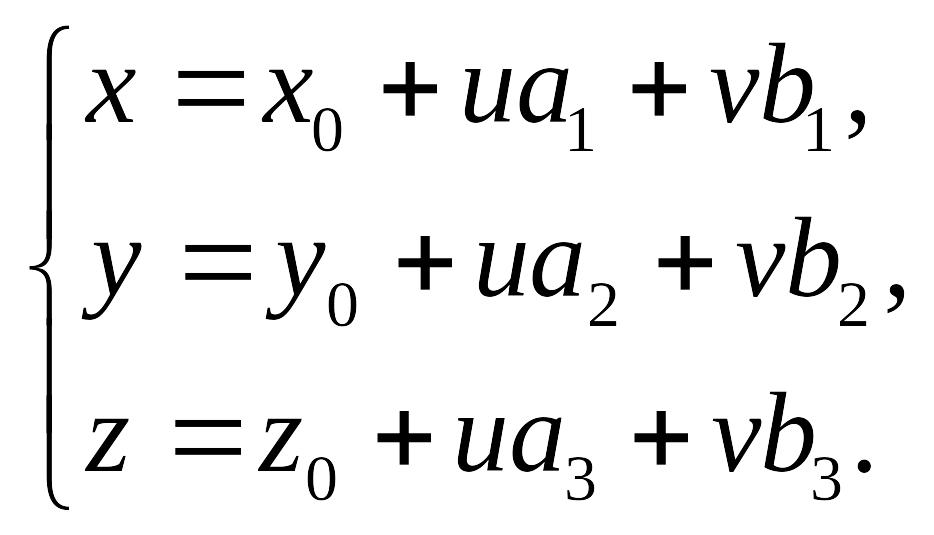 (14.4)
(14.4)
Уравнения (14.4) называются параметрическими уравнениями плоскости.
Условие
компланарности векторов
можно выразить через смешанное
произведение этих векторов:
![]() ,
или в координатной форме:
,
или в координатной форме:
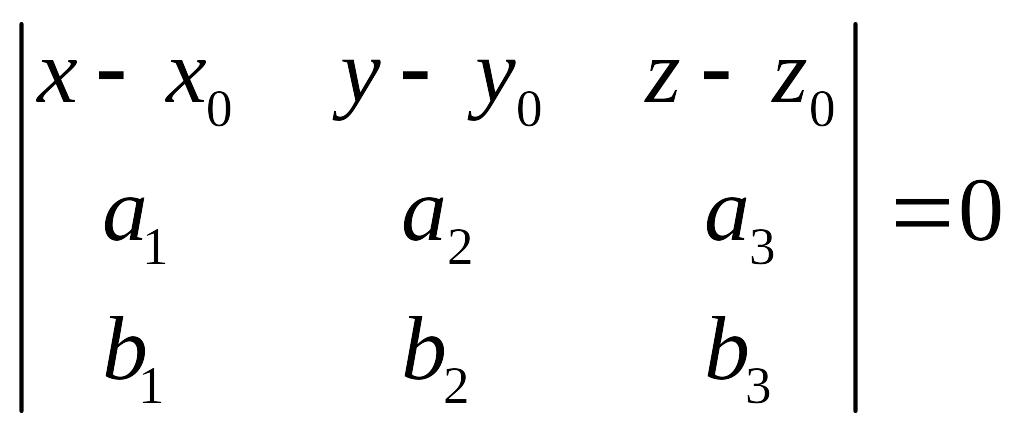 (14.5)
(14.5)
Уравнение
(14.5) –
уравнение плоскости, проходящей через
точку
с заданными направляющими векторами
и
![]()
Плоскость
однозначно определяется тремя точками
![]()
![]() не
лежащими на одной прямой. В этом случае
не
лежащими на одной прямой. В этом случае
![]() и
и
![]() –
направляющие векторы плоскости
–
направляющие векторы плоскости
![]()
![]() Тогда из уравнения (14.5) получаем:
Тогда из уравнения (14.5) получаем:
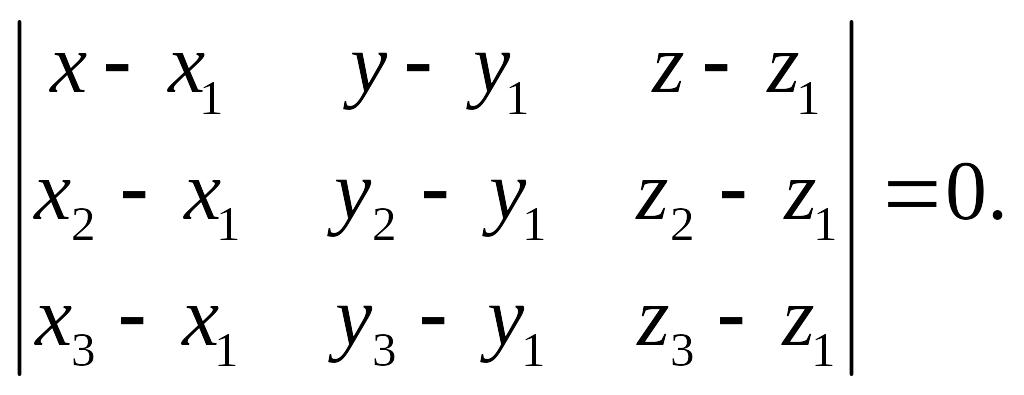 (14.6)
(14.6)
Уравнение (14.6) носит название уравнения плоскости, проходящей через три точки.
Пусть,
в частности, известны точки, в которых
плоскость
пересекает оси координат:
|
Рис. 14.3 |
После раскрытия определителя получаем:
![]()
![]() (14.7)
(14.7)
Уравнение (14.7) называется уравнением плоскости в отрезках на осях.
Взаимное расположение плоскостей в пространстве.
Рассмотрим
плоскости
![]() и
и
![]() Их взаимное расположение характеризуется
углом между ними. Этот угол однозначно
определяется углом между нормальными
векторами этих плоскостей
Их взаимное расположение характеризуется
углом между ними. Этот угол однозначно
определяется углом между нормальными
векторами этих плоскостей
![]() и
и
![]() Обозначим через
- угол между нормальными векторами.
Тогда:
Обозначим через
- угол между нормальными векторами.
Тогда:
![]() (14.8)
(14.8)
Замечание. Обратим внимание, что угол между плоскостями не обязательно равен , он может быть равен и (рис. 14.4-14.5).
|
|
Таким образом, формула (14.8) определяет значение косинуса угла между плоскостями с точностью до знака. Косинус острого угла между плоскостями и может быть найден по формуле:
![]() (14.9)
(14.9)
Заметим,
что
![]()
![]()
![]() .
.

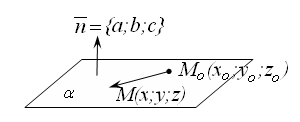
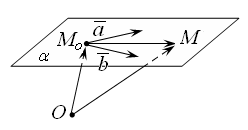
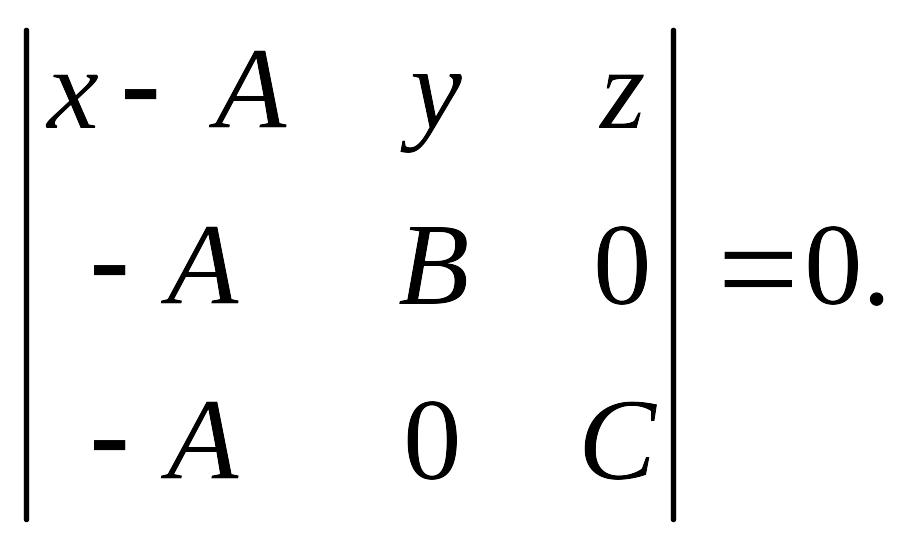

 Рис.
14.4
Рис.
14.4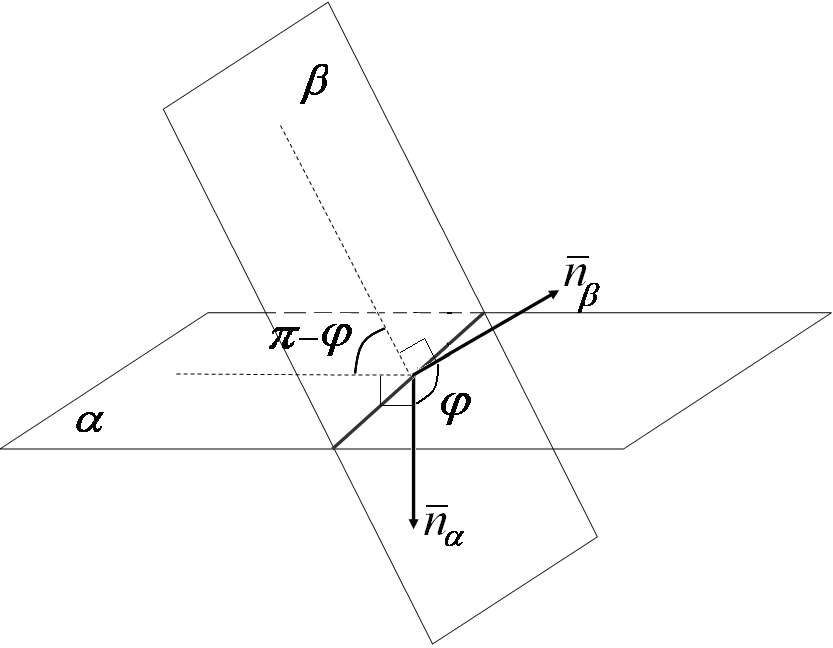 Рис.
14.5
Рис.
14.5