Алгебраическая форма записи комплексных чисел

Обозначим . Тогда .

Таким образом, число i является корнем уравнения

Перейдем к другой, более удобной форме записи комплексных чисел. Очевидно, .

Def. Если комплексное число записано в виде , то такую форму записи называют алгебраической формой записи комплексного числа.

Число i называют мнимой единицей, действительной частью числа z , мнимой частью числа z Числа вида называют чисто мнимыми числами.

Def. Пусть . Числом, сопряженным z, называется число

Операции 8.2 - 8.5 определяются для комплексных чисел, записанных в алгебраической форме следующим образом:

; (8.6)

; (8.7)

; (8.8)

(8.9)

Символ i для мнимой единицы предложил Л. Эйлер в 1777, взявший для этого первую букву слова лат. imaginarius. Ему же принадлежит мысль об алгебраической замкнутости поля комплексных чисел (1751), но строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Нет необходимости запоминать эти формулы. Можно заметить, что достаточно лишь раскрыть скобки и привести подобные слагаемые относительно действительных и мнимых частей. При умножении комплексных чисел, записанных в алгебраической форме, следует формально перемножить выражения (как двучлен на двучлен), учитывая, что , а затем выделить действительную и мнимую части полученной суммы.

Выполнение операции деления легко формализуется, если предварительно числитель и знаменатель умножить на число сопряженное с числителем. Действительно,

N. 1)

2)

Th.8.1

(свойства операции сопряжения) 1. 2. 3. 4.

Доказательство.

1.

.

2.

Таким образом, .

3.

Таким образом, .

4.

Таким образом, .

Геометрическая интерпретация комплексных чисел

В основе геометрической интерпретации поля комплексных чисел лежит возможность поставить каждому комплексному числу поставить в соответствие точку плоскости с координатами . Между элементами поля С и точками плоскости с выбранной декартовой системой координат можно установить взаимно-однозначное соответствие. При этом действительные числа изображаются точками оси Ох, а чисто мнимые – точками оси Оу. Поэтому ось Ох называется действительной осью, а ось Оу – мнимой осью. Плоскость, на которой изображают комплексные числа, называют комплексной плоскостью. Таким образом, через z обозначают как комплексное число, так и точку плоскости, которая изображает это число.

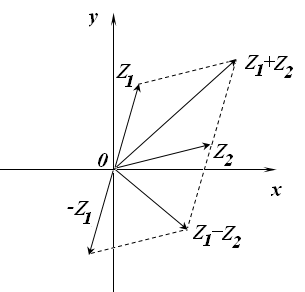
Комплексное число рассматривают радиус-вектор точки z комплексной плоскости.

Заметим, что операции сложения и вычитания комплексных чисел хорошо интерпретируются на комплексной плоскости. Сложение комплексных чисел выполняется по правилу сложения векторов (правилу параллелограмма). Аналогично интерпретируется и операция вычитания (рис. 8.1). Число противоположное , будет точкой комплексной плоскости сим­метричной точке z относительно начала координат. Число сопряженное с числом

Рис. 8.1.

z изображается точкой, симметричной точке z относительно оси Ох.

Заметим, что для комплексных чисел понятия «больше», «меньше» не могут быть определены, т.к. они, в отличие от действительных чисел, расположены не на прямой, точки которой естественным образом упорядочены, а на плоскости.

Th.8.2

Если – комплексные числа, то имеют место соотношения: (8.10) (8.11)

Доказательство.

Неравенство (8.10) вытекает непосредственно из неравенства треугольника (известной из курса элементарной геометрии), ввиду того, что имеем треугольник (рис. 8.1) со сторонами

Поскольку и , то из неравенства (8.10) вытекает неравенство (8.11) .

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНЫХ ЧИСЕЛ. ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ. ФОРМУЛА МУАВРА. ИЗВЛЕЧЕНИЕ КОРНЯ n-ОЙ СТЕПЕНИ ИЗ КОМПЛЕКСНОГО ЧИСЛА.

Тригонометрическая форма записи комплексных чисел. Действия с комплексными числами в тригонометрической форме

Пусть произвольное комплексное число, которое изобразим на комплексной плоскости (рис. 9.1). Обозначим , а угол между положительным напрвлением оси Ох и вектором через . Def. Число r называется модулем, а угол аргументом комплексного числа z. Обозначают:

Рис. 9.1.

В отличие от модуля аргумент комплексного числа определяется неоднозначно (с точностью до ).

Абрахам де Муавр (26.05.1667 — 27.11.1754) - английский мате­матик французского происхождения. Кроме правила возведения в n-ю степень и извлечения корня n-й степени для комплексных чисел, исследовал степенные ряды, первый пользовался возведением в степень бесконечных рядов. В теории вероятностей доказал частный случай теоремы Лапласа .

Def. Значение из интервала называют главным значением аргумента и обозначают Таким образом,

Из прямоугольного (рис. 9.1) , Получаем, что т.е.

(9.1)

где (9.2)

Представление комплексного числа в виде (9.1) носит название тригонометрической формы записи комплексного числа.

N. Представьте число в тригонометрической форме.

Решение.

У нас

.

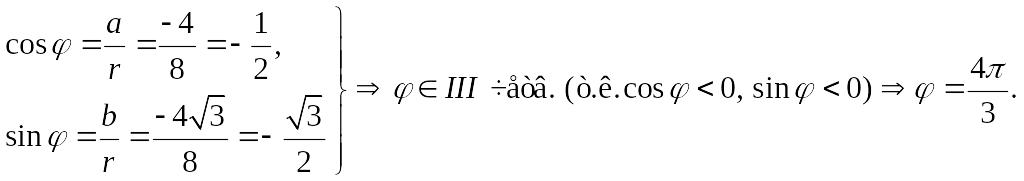Тогда, .

Th.9.1

Если и , то (9.3) (9.4)

Доказательство.

.

Th.9.2

(формула Муавра) Если , то для всех (9.5)

Доказательство.

Рассмотрим случай, когда В этом случае формула (9.4) непосредственно следует из формулы (9.3).

Пусть Тогда:

Таким образом, формула (9.4) справедлива для

Получили, что формула (9.5) верна для всех . Эта формула носит название формулы Муавра .

N. Даны числа

Вычислить: а) б) в)

Решение.

а)

б)

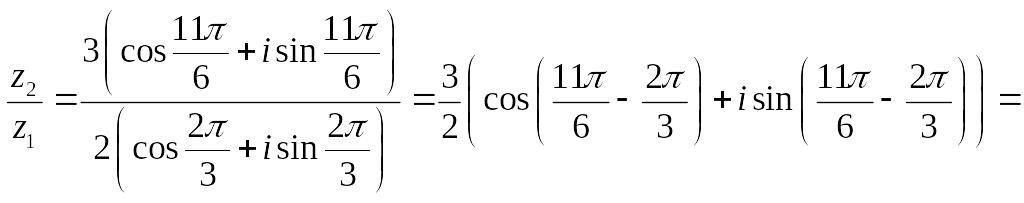
в)

.