
- •Санкт-петербургский государственный университет физический факультет
- •С.В.Карпов фононы в кристаллах и гетероструктурах
- •Санкт-Петербургский государственный университет
- •Фононы в кристаллах и гетероструктурах
- •1. Симметрия кристаллов
- •1.1. Кристаллическая решетка
- •1.2. Элементы симметрии кристалла
- •Типы плоскостей скольжения
- •1.3. Сингонии и кристаллические классы
- •Кристаллические системы – сингонии
- •1 Тип решетки Браве
- •1 Тип кристаллического класса
- •1 Тип выбора частичной трансляции r для каждой операции группы r
- •Распределение кристаллических классов по сингониям
- •1.4. Классификация возбуждений в кристаллах
- •Неприводимые представления группы трансляций
- •1.5. Классификация возбуждений для фактор-группы
- •2. Ристаллический периодический потенциал
- •2.1. Общая модель твердого тела. Гамильтониан
- •2.2. Адиабатическое приближение
- •3. Зонные состояния периодических систем
- •3.1. Линейная моноатомная цепочка
- •Постановка решения в виде функции Блоха
- •3.2. Дисперсионные соотношения (закон дисперсии)
- •Двухпроводная электрическая линия
- •2. Акустические колебания в системе резонаторов
- •3. Связанные маятники
- •Электромагнитные волны в атмосфере
- •5. Многоатомная линейная цепочка
- •Однородный упругий стержень и стержень с периодической плотностью
- •Волны де-Бройля
- •3.3. Уравнение Матье и зонная структура
- •3.4. Фазовая и групповая скорость волн в диспергирующей среде
- •4. Фононы в идеальных кристаллах
- •4.1. Линейная двухатомная цепочка
- •4.2. Колебания трехмерной решетки
- •4.3. Обратная решетка и зона Бриллюэна
- •4.4. Ход ветвей колебаний в зоне
- •4.5. Расчеты колебаний кристаллов
- •Как известно, коэффициенты Lkl являются элементами матрицы, для которой выполнено:
- •4.6. Функция распределения плотности частот
- •Особенности функции g(), обусловленные различными критическими точками
- •5. Полярные колебания в кристаллах
- •5.1. Продольные и поперечные акустические колебания
- •Поэтому:
- •5.2. Поперечные и продольные оптические колебания
- •5.3. Соотношения Лиддейна-Сакса-Теллера
- •Отсюда следует, что
- •5.4. Реальные состояния. Эффект "запаздывания". Поляритон
- •Первые два уравнения, как известно, дают
- •6. Квантовомеханическое представление колебаний
- •6.1. Нормальные колебания.
- •6.2. Фононы
- •6.3. Гармонический осциллятор
- •Решение стационарного уравнения Шредингера
- •6.4. Операторы рождения и уничтожения фононов
- •6.5. Ангармонический осциллятор и кристалл
- •6.6. Фонон-фононные взаимодействия
- •7.1. Низкоразмерные 3d, 2d, 1d, 0d системы
- •7.2. Фононы в объемных и ограниченных структурах
- •7.3. Размерно-ограниченные кристаллические среды.
- •7.4. Приближение упругого континуума.
- •7.5. Рамановское рассеяние на сложенных акустических фононах (folding phonons)
- •7.6. Приближение механического континуума.
- •7.7. Рамановское рассеяние на квантованных оптических фононах
- •7.8. Приближение диэлектрического континуума
- •7.9. Рамановское рассеяние на интерфейсных модах
- •8.1. Модель упругого континуума. Лэмбовская мода
- •8.2. Модель механического континуума
- •8.3. Модель диэлектрического континуума
- •8.4. Расчеты колебательных спектров нанокристаллов
- •Оглавление
- •I. Симметрия и структура кристаллов
- •II. Кристаллический периодический потенциал
- •III. Зонные состояния периодических систем
2. Ристаллический периодический потенциал
2.1. Общая модель твердого тела. Гамильтониан
В основе наших представлений о твердом теле лежат следующие основные понятия: твердое тело есть система многих взаимодействующих частиц, динамика которых подчиняется законам квантовой механики; основой твердого тела является кристаллическая решетка, структура которой зависит от его свойств симметрии. Кристаллическое тело представляет собой совокупность огромного числа атомных ядер и электронов.
Проблему определения собственных состояний такой системы легко сформулировать, но, к сожалению, нельзя точно решить. Стационарные состояния кристалла описываются уравнением Шредингера:
H (ri,Rk)Е (ri,Rk)
с гамильтонианом
Ĥ=Ĥel+Ĥion+Ĥel-ion .
В этом выражении Ĥel – оператор кинетической и потенциальной энергии электронов, Ĥion– оператор кинетической и потенциальной энергии ионов и Ĥel.ion – оператор, описывающий взаимодействие электонов с ионами.
![]() .
.
Здесь ri и rj– координаты i-го и j-го электрона, Rk и Rl – координаты k-го и l-го иона или атомного остатка, первый член описывает кинетическую энергию электронов, второй – кинетическую энергию ядер. Оператор i действует только на координаты электронов ri, а k только на координаты ядер Rk. Третий член – потенциальная энергия взаимодействия атомных остатков с зарядами Zke и Zle между собой, а Rk и Rl – их координаты; следующий член – потенциальная энергия притяжения ядер и электронов, а последний член – энергия отталкивания электронов. Упрощение сформулированной задачи можно получить, учитывая различие в массах ядер и электронов, т.к. (m/M)<<1.
Уравнение Шредингера содержит 3ZN переменных, если через N обозначить число атомов в кристалле, а через Z – число электронов. Так как в 1 см3 содержится примерно 5*1022 атомов, то при Z, равному 10, число переменных составляет 5*1023 см–3.
Ясно, что такое уравнение не может быть решено в общем виде. Это связано не только с техническими вычислительными трудностями, но и с трудностями принципиальными, поскольку современная квантовая механика по существу не имеет аппарата при решении задач для системы с большим числом частиц.
2.2. Адиабатическое приближение
Для дальнейшего исследования многочастичного уравнения Шредингера с целью получения его приближенных решений необходимо принять во внимание физические свойства электронов и ядер. Возможно только приближенное квантовомеханическое описание таких систем. Основным приближением, используемым в теории твердого тела, является адиабатическое приближение или приближение Борна-Оппенгеймера, учитывающее различный характер движения легких (электронов) и тяжелых (ядер) частиц. В термодинамическом равновесии из-за различия масс электронов и атомных остатков (ядер) скорости движения эти частиц различны. Для быстро движущихся электронов важно мгновенное положение ядер, в то время как для медленно движущихся ядер оказывает влияние не мгновенное положение электронов, а только их усредненное движение. Это утверждение легко понять применительно к многоэлектронным атомам. Ясно, движение ядра в силу его инерционности не следует за движением каждого электрона, а движется в усредненном поле всех электронов. В то же время сравнительно медленное движение ядра увлекает за собой электроны, вследствие чего целостность атома сохраняется. Подобное же положение должно иметь место и в кристалле. Другими словами, волновую функцию электронов в кристалле можно получить, решая стационарное уравнение Шрёдингера для конкретного положения ядер. При изменении положения ядер необходимо снова решить уравнение Шрёдингера, изменив координаты ядер, и сшить получившуюся волновую функцию с полученной ранее. Волновую функцию, описывающую состояния ядер, можно получить при решении уравнения Шрёдингера, в котором введено среднее поле электронов, действующих на атомные остатки. Математическая формулировка этих утверждений состоит в том, что полную волновую функцию кристалла (ri,Rk) нужно представить в виде произведения волновой функции электронов и ядер:
(ri,Rk)=Ф(ri,Rk) (Rk),
в котором в волновой функции электронов Ф(ri,Rk) координаты ядер Rk являются по своей сути параметрами. Подставляя такую волновую функцию в уравнение с полным гамильтонианом Ĥ, и учитывая, что
2k Ф = 2k Ф +2kФ k + Ф 2k ,
уравнение Шрёдингера распадется на два уравнения для электронов и атомных остатков.
Первое уравнение – это уравнение для электронов:
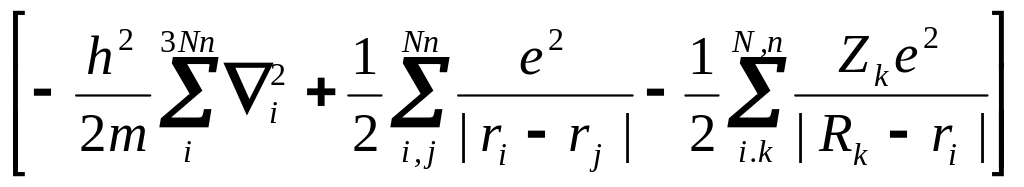 =Ф(ri,Rk)=
(Rk)Ф(ri,Rk),
=Ф(ri,Rk)=
(Rk)Ф(ri,Rk),
где представляет собой энергию электронов, движущихся в поле покоящихся ядер.
Второе уравнение
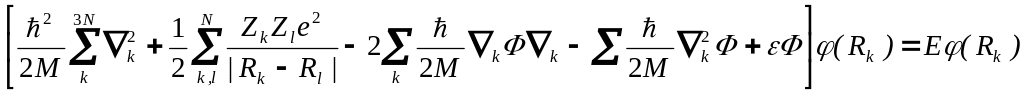
точно описывает ядерную систему кристалла, если в этом гамильтониане пренебречь вторым и третьим членами.
Полную энергию электронной системы можно получить, умножив первое уравнение на функцию Ф*(ri,Rk), сопряженную волновой функции электронной подсистемы, и интегрируя по конфигурационному пространству d (координатам электронов) с учетом нормировки Ф*(ri,Rk) Ф(ri,Rk)d :
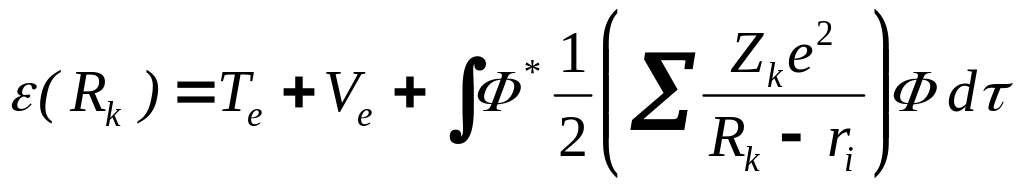 .
.
Здесь Te и Ve представляют собой среднюю кинетическую и потенциальную энергию электронов, а последний член этого выражения является средней энергией взаимодействия электронов и ядер, т.е. атомных остатков с пространственным зарядом, создаваемым электронами.
Во втором уравнении Шрёдингера, описывающем состояние ядерной подсистемы, действительно можно пренебречь вторым и третьим членом в гамильтониане. Легко получить полную среднюю энергию ядерного движения. Если умножить это уравнение слева на функцию *(Rk), сопряженную волновой функции ядерной подсистемы, и проинтегрировать по координатам ядер, то с учетом нормировки функций *(Rk) для энергии движения ядер кристалла получим выражение:
![]() .
.
Здесь TR и VR представляют собой среднюю кинетическую и потенциальную энергию ядер, а два последних члена этого выражения – некоторую добавку, связанную с наличием электронной подсистемы.
Первый
из этих членов![]()
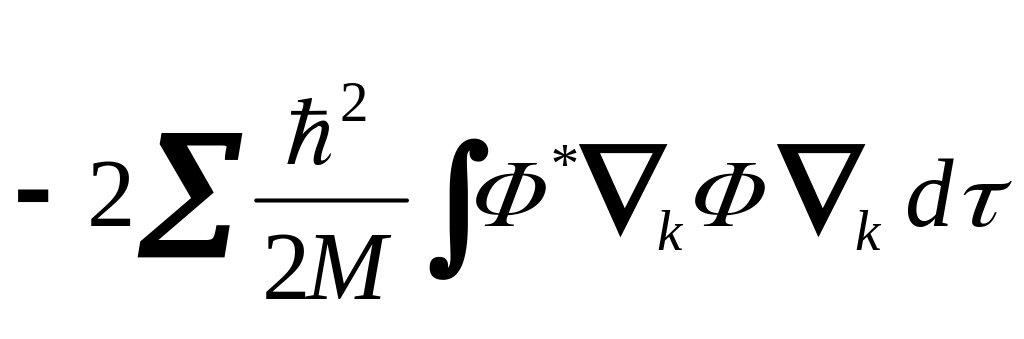
определяет среднюю энергию электронов при изменении положения ядер в кристалле, поскольку в него входит величина kФ(ri,Rk). Из-за того, что Ф(ri,Rk) слабо зависит от Rk , средняя величина этого члена, определяющего электрон-фононное взаимодействие, равна нулю. Действительно, в этом легко убедиться:
![]() .
.
Второй член в выражении для средней энергии ядер мал, поскольку волновая функция Ф(ri,Rk) слабо зависит от координат атомов Rk из-за малости отношения массы электрона к массе атомного ядра m/M. Поэтому вторая производная по Rk мала, а сам член меньше остальных в m/M раз. В худшем случае сильной связи между электронами и атомными остатками выполнено Ф(ri,Rk) = Ф(ri–Rk), т.е.
![]() .
.
Поэтому оценка этого члена дает:
![]() ,
,
где Te – средняя кинетическая энергия электронов. Этим членом по сравнению с полной энергией движения атомных остатков Е можно пренебречь; ошибка, вносимая при этом в выражение для энергии кристалла, крайне мала; она составляет величину порядка отношения массы электрона к массе ядра, которая для Ge, например, составляет величину около 10–5.
С учетом этих оговорок уравнение Шрёдингера для кристалла распадается на два уравнения – для электронов и атомных остатков (ядер).
Мы выбрали при этом самый «невыгодный» случай, когда волновая функция электронов представляется комбинацией атомных волновых функций (так называемое приближение сильно связанных электронов). Если бы волновая функция электронов не зависела от координат ядер (приближение свободных электронов), то обе поправки в уравнении Шредингера были бы равны нулю точно.
Таким образом, мы приходим к выводу, что, отбрасывая обе поправки, мы делаем пренебрежимо малую ошибку величине энергии Е (для германия она составляет примерно 0,3). Окончательно можно сказать, что в данном приближении, полная энергия кристалла с большой точностью совпадает с собственным значением ядерной части гамильтониана. Из сказанного видно, что адиабатическое приближение для кристалла с обычным гамильтонианом приводит к достаточно точному значению энергии, если предположить, что волновая функция кристалла может быть записана в виде
(ri,Rk)=Ф(ri,Rk) (Rk),
причем Ф(ri,Rk) и (Rk) находятся из уравнений:
He(ri,Rk)=Еe(ri,Rk),
H Ф(ri,Rk) = Е Ф(ri,Rk) .
В адиабатическом приближении волновая функция электронов определяется мгновенным положением ядер, в то время как волновая функция ядер определяется усредненным полем электронов.
