6. Волны де-Бройля

Дисперсионное соотношение справедливо также для квантовых частиц, описываемых волнами де-Бройля. Частице с импульсом p соответствует волновой вектор k, определяемый из соотношения p=hk. Кроме того, частица с энергией Е имеет волновую частоту , поскольку E=h. Объединяя эти два соотношения, можно получить классическое соотношение между энергией Е и волновым вектором k для частицы с массой m:

.

Для частицы, помещенный в одномерный "ящик" длины L, возможными состояниями являются нормальные волны де-Бройля, т.е. стоячие волны, у которых частота и длина волны связаны указанным уравнением (рис. 17).

Такие стоячие волны де-Бройля имеют такую же последовательность конфигураций, что и моды идеальной струны, поскольку на границе (и вне) интервала L вероятность нахождения частицы равна нулю. В то же время частоты не являются гармониками частоты самой низкой моды, как это имеет место для идеальной струны:

.

Таким образом, частота волн де-Бройля пропорциональна не номеру гармоники, как это имеет место для идеальной струны, а квадрату номера гармоники (квадрату квантового числа). Зависимость частоты волны де-Бройля или энергии электрона, движущегося в свободном пространстве, от волнового вектора k показана на рис.18. Она представляет собой параболу, поскольку волновой вектор может принимать всевозможные значения.

В среде с периодическим потенциалом V(x) = V(x+x_n) движение электрона с массой m в одномерном случае описывается следующим уравнением Шредингера

.

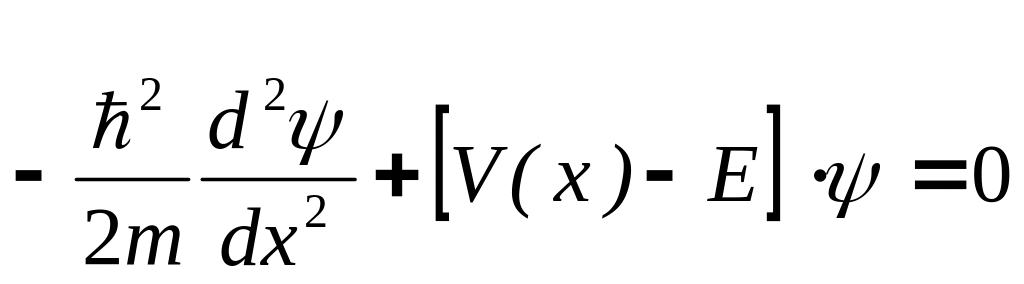Здесь ћ– постоянная Планка, а E – собственные значения энергии.

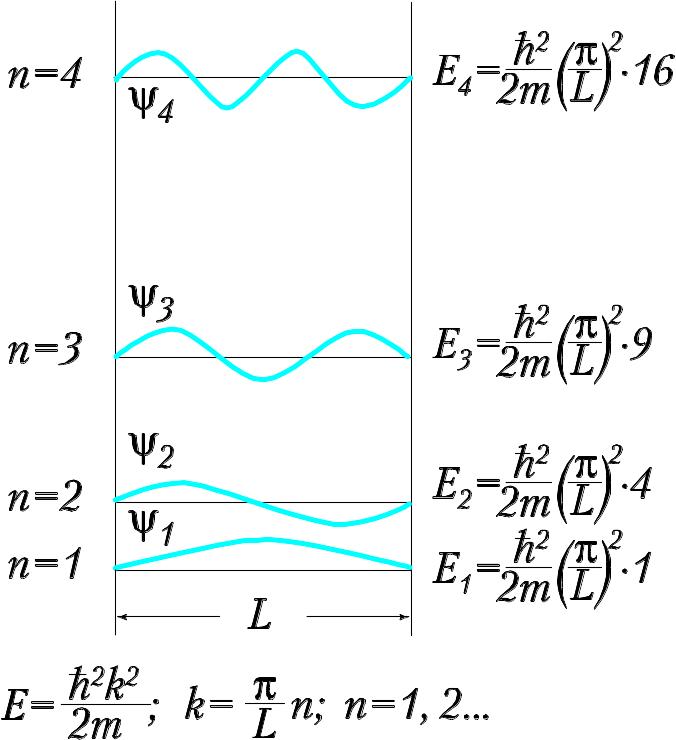
Рис. 17. Волны де-Бройля в одномерном ящике длины L. Энергии таких состояний растут как квадраты натуральных чисел n, в то время как частоты, а значит и энергии механических колебаний струны, растут пропорционально номеру гармоники n: =(С₁₁/)^1/2k=(С₁₁/)^1/2(2/) =(С₁₁/)^1/2(2/2L)n.

В кристаллической решетке по­тенциал V(x) создается положительными зарядами ионов, рас­положенных в узлах решетки, и отрицательным облаком электронов, расположенных между ионами. Такой потенциал в объемном кристалле является периодической функцией трех переменных x, y, z с перио­дами d₁, d₂, d₃, определяемыми структурой кристалла. Экспоненциальный показатель k в волновой функции ψ~ exp(–ikx) как и в случае механических волн, также может принимать как действительные, так и комплексные значения. Это приводит к появлению разрывов в параболической дисперсионной зависимости, характерной для свободного электрона. Даже появление бесконечно малого периодического возмущения приведет к существованию разрывов на дисперсионной кривой при значениях волнового вектора k, кратных π/d. В этом случае нет необходимости рассматривать всевозможные значения волнового вектора, и функциональную зависимость E=ћ²k²/2m удобно рассматривать только в первой зоне Бриллюэна, как это показано на рис. 18. При увеличении значения периодического потенциала, в котором движется электрон, зоны с комплексными значениями волнового вектора k, где происходит затухание, останутся при тех же самых значениях k, однако величина разрывов будет возрастать. Поэтому всегда будут чередоваться разрешенные по энергиям зоны и запрещенные.

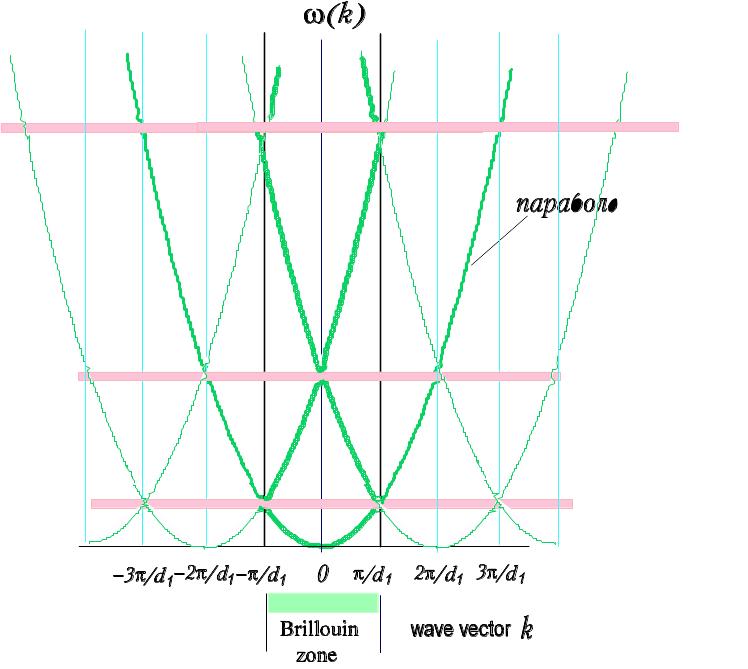
Рис. 18. Дисперсионная зависимость для волн де-Бройля в случае свободного пространства (парабола) и в случае периодического потенциала. В последнем случае на графике появляются разрывы при значениях волнового вектора k, кратного величине π/d. В энергетическом интервале в области разрыва решениям соответствуют комплексные значения волнового вектора k, так что для определенных значений энергии де-Бройлевская волна электрона будет затухающей. Эти значения энергии представляют собой запрещенные зоны, которые чередуются с разрешенными. Дисперсионные зависимости удобно представлять многозначной функцией в области периодичности волнового вектора – в зоне Бриллюэна.

Структура зон не зависит от частных физических предположений о природе рассматриваемых волн — она одинакова как для электронных волн де-Бройля, так и для механических или упругих волн, или для электромагнитных (рентгеновских) волн. Это общий результат, и он не зависит от физической природы волн.