Добавил:

sutkowska92 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бухарский инженерно-технологический институт

Предмет:

Высшая математика

Файл:

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf

Скачиваний:

331

Добавлен:

27.05.2019

Размер:

4 Мб

Скачать

☆

<<< < Предыдущая 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3729 30 31 32 33 34 35 36 37 > Следующая >>>

19.5 Производная функции, заданной параметрическими уравнениями

Зададим две функции одной и той же переменной t ; обозначим их через x и y :

x = x(t) , y = y(t) .

(*)

Задание этих функций означает задание функциональной зависимости между переменными x и y . В самом деле, для каждого значения t (в неко-

торой области) из системы (*) находятся значения x и y , которые и являются соответствующими друг другу.

Определение. Задание функциональной зависимости между двумя переменными, состоящее в том, что обе переменные определяются каждая в отдельности как функция одной и той же вспомогательной переменной, называется параметрическим, а вспомогательная переменная – параметром.

Отыскание по системе (*) непосредственной связи между переменными x и y без участия переменной t называется исключением параметра.

Пример 2.

x = t,

Пусть функция задана параметрическим уравнениями:

y = cos t.

Исключая параметр t , получим y = cos x .

Замечание. Не всегда можно провести операцию исключения параметра. Например, если хотя бы одна из функций системы (*) постоянна.

Теорема.

Пусть функция

y = f (x) , определенная в

O(x0 ) , задается

параметрическими уравнениями

x = x(t),

где

x(t)

и y(t)

–

дифференци-

y = y(t),

руемые функции в точке t0

( x0 = x(t0 ) ), причем функция x(t)

монотонна в

O(t0 ) . Тогда функция y = f (x)

дифференцируема в точке x0 и имеет место

следующая формула:

yt′

y′x =

Доказательство.

xt′

lim

yt′(t)

y′x = lim

= lim

t→0

x′(t)

x→0

lim

t→0

(функция x = x(t)

– дифференцируема, следовательно, непрерывна, следова-

тельно, функция

t = t(x) – непрерывна, следовательно, lim

t = 0 ).

x→0

19.6 Геометрический смысл производной

Определение. Касательной M 0T к линии L в ее точке M 0 (рис. 3.20) называется предельное положение прямой, проходящей через точ-

ку M 0 и другую точку

M линии, когда эта точка M стремится слиться с

данной точкой M0 .

Теорема.

Если значение производной от функции y = f (x)

при x = x0

равно f ′(x0 ) , то прямая,

проведенная через точку M0 (x0 ; y0 ) с угловым ко-

эффициентом,

равным

f ′(x0 ) , является касательной к графику функции в

точке M0 .

Доказательство. Проведем через точку M0

(рис. 3.20) прямую M0T с уг-

ловым коэффициентом

f ′(x0 ) , это значит, что

f ′(x0 ) = tgα , где α – угол на-

клона прямой

M0T к оси абс-

цисс. Придадим затем x0 при-

y0 + y

ращение

x ,

возьмем

точку

M , лежащую на графике

M 0

функции

и соответствующую

значению

аргумента

x0 + x ,

проведем секущую M0 M . Уг-

ловой коэффициент этой секу-

x0 + x

щей равен

y , где

M0 R

Рис. 3.20

y = f (x0 + x) − f (x0 ) .

Пусть теперь

x → 0 , то-

гда точка M будет стремиться по линии L к точке M 0 . Секущая M0 M при

этом поворачивается вокруг точки M0

и ее угловой коэффициент стремится

по условию теоремы к определенному пределу

lim

y =

f ′(x0 ) ,

(*)

x→0

равному угловому коэффициенту прямой M0T . По формуле для тангенса уг-

ла между двумя прямыми ( M0T и M0 M )

f ′(x0 ) −

tg TM 0 M =

1+ f ′(x0 )

В силу равенства (*) при

x → 0 числитель дроби стремится к нулю, а зна-

менатель – к числу 1+[f ′(x0 )]2 ≠ 0 . Поэтому tg TM0 M стремится к нулю, а значит, и сам TM 0M тоже стремится к нулю. Таким образом, прямая M 0T является касательной.

Геометрический смысл производной. Значение производной f ′(x0 ) равно угловому коэффициенту касательной к графику функции y = f (x) в точке с абсциссой x0 .

19.7 Уравнения касательной и нормали к линии

Составим уравнение касательной к линии l , являющейся графиком функции y = f (x) в ее точке M0 (x0 ; y0 ) , где y0 = f (x0 ) (рис. 3.21). Т.к. каса-

тельная проходит через точку M0 (x0 ; y0 )

и имеет угловой коэффициент, равный

f ′(x0 ) , то ее уравнение имеет вид

y − y0 = f ′(x0 )(x − x0 ) .

(1)

Определение.

Нормалью к линии

в ее точке M0 называется прямая, про-

ходящая

через точку M 0 перпендику-

лярно касательной данной линии, по-

Рис. 3.21

строенной в точке M0 .

Т.к. нормаль к линии l в точке M 0

проходит через точку

M0 (x0 ; y0 ) и имеет угловой коэффициент,

равный

−

, то ее уравнение имеет вид

′

(x0 )

y − y

= −

(x − x ) .

(2)

f ′(x0 )

19.8

Дифференцирование элементарных функций

y = C – const :

y′ = 0 .

Доказательство.

lim

y =

lim

y(x +

x) − y(x)

= lim

= 0 .

x→0

y = ax :

y′ = ax ln a .

Доказательство.

= lim ax+ x − ax = ax

lim a x

−1

x −1 = t,

lim

x = loga (t +1),

x→0

x → 0, t

→ 0

= a x lim

= (*) =

ax =

a x = a x ln a .

loga e

ln e

t→0 loga (t +1)

ln a

100

(*):

loga (t +1)

1 t

→ loga e .

loga (t +1) = loga (t +1)

t →0

Таким образом,

′

ln a .

) = a

y = ex :

y′ = ex

(частный случай п.2).

y = loga x :

y′ =

ln a

Доказательство.

x +

log

loga (x +

x) −loga x

y′ = lim

= lim

x→0

log

= lim

log

x→0

→0

x→0

x x x

loga e ==

ln e

lim loga 1

ln a

x ln a

x→0

Таким образом,

(loga

x)′ =

x ln a

y = ln x :

y′ = 1x

(частный случай п.4).

y = sin x :

y′ = cos x .

Доказательство.

y′ = lim sin(x +

x) −sin x =

sinα −sin β = 2sin α − β

cos α + β

→0

2sin

cos

2x +

sin

lim cos x +

=1 cos x = cos x .

= lim

x→0

(sin x)′ = cos x .

Таким образом,

y = cos x :

y′ = −sin x .

Доказательство.

y′ = lim cos(x +

x) −cos x

cosα −cos β = −2sin α − β sin

α + β

x→0

− 2sin

sin x +

sin 2

= lim

= − lim

lim sin x +

x→0

= −1 sin x = −sin x .

Таким образом,

(cos x)′ = −sin x .

8. y = tg x :

y′ =

cos2 x

Доказательство.

′

sin x

′

sin x

(sin x)

cos x −(cos x)

′

= (tg x)

= cos x

cos2 x

cos x cos x +sin x sin x

cos2

x +sin2

cos2 x

101

2x =

′

Таким образом, (tg x)

cos2 x

y = ctg x :

′

= − sin2 x .

Доказательство.

′ cos x

′

cos x

(cos x) sin x −(sin x)

′

(ctg x) = sin x

sin2 x

−sin x sin x −cos x

cos x

−sin2 x −cos2 x

= −

sin2 x

sin2

′

Таким образом, (ctg x)

= −

sin2 x

10.

y = arcsin x :

′

1− x2 .

Доказательство. Пусть

y = arcsin x ,

тогда

x = sin y

– обратная функция.

Отсюда

(x( y))′ = cos y . Следовательно,

по теореме о производной обратной

функции:

′

(y(x)) =

(x( y))′

cos y

1−sin2 y

1− x2

Таким образом, (arcsin x)′ =

− x2

102

Замечание. Корень берется со знаком “+”, потому что значения функции y = arcsin x лежат в интервале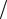 (−π2; π2), а cos y в этом интервале положи-

телен. При y = ±π 2 , т.е. для x = ±1

производной не существует, хотя сама

функция y = arcsin x в этих точках определена.

11.

y = arccos x :

′

= −

1− x2 .

Доказательство.

Пусть

y = arccos x , тогда

x = cos y

– обратная функция.

Следовательно:

′

(y(x))

= −

(x( y))′

−sin y

1−cos2 y

1− x2

Таким образом, (arccos x)′ = −

1− x2

12.

y = arctg x :

y′

1+ x2

Доказательство.

Пусть

y = arctg x ,

тогда

x = tg y

–

обратная функция.

Следовательно:

′

(y(x))

= cos

(x( y))′

cos2 y

′

Таким образом, (arctg x)

1+ x2

13. y = arcctg x :

′

= −1

+ x2 .

Доказательство. Пусть y = arcctg x , тогда Следовательно:

y =	1	=	1	.
y =	+ tg2 y	=	+ x2	.
1	+ tg2 y	1	+ x2

x = ctg y – обратная функция.

′

(y(x))

= −sin

y = −

= −

(x( y))′

−

1+ ctg2 y

1+ x2

sin2 y

′

Таким образом,

(arcctg x) = −

1+ x2

14. y = xn :

y′ = n xn−1 .

Доказательство.

Пусть y = xn ,

тогда xn = eln x n

= en ln x . Следовательно:

(xn )′ = (en ln x )′ = en ln x (n ln x)′ = n en ln x (ln x)′ = n en ln x 1

= n xn x−1 = n xn−1 .

(xn )′ = n xn−1 .

Таким образом,

<<< < Предыдущая 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3729 30 31 32 33 34 35 36 37 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
27.05.20194 Мб331КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf
#
27.05.20192 Мб265КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf
#
27.05.201920 Мб11180Письменный Д.Т. Конспект лекций по высшей математике - Полный курс.pdf