Добавил:

sutkowska92 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бухарский инженерно-технологический институт

Предмет:

Высшая математика

Файл:

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf

Скачиваний:

250

Добавлен:

27.05.2019

Размер:

3.56 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 3724 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

6)	Рассмотрим две функции y = f (u) и u =ϕ(x) .

Функция y = F(x) , заданная по правилу: каждому x ставится в соот-

ветствие y = f (ϕ(x)) , называется сложной функцией относительно перемен-

ной x , u при этом называется промежуточным аргументом сложной функции.

§ 3. Абсолютные величины и соотношения, связанные с ними

Определение. Абсолютной величиной (или модулем) действительного числа a называется: само число a , если a – положительное число; нуль, если число a – нуль; число, противоположное числу a , если a – отрицательное число, т.е.:

a =

a, если a > 0, 0, если a = 0,

− a, если a < 0.

Свойства модуля действительного числа

a + b

≤

a b

(b ≠ 0 ).

a − b

≥

−

§ 4. Последовательность. Характер изменения переменных величин

Пусть дано некоторое множество чисел, расположенных в определенном порядке:

2 , 4 , 8 , …, 2n , …

(1)

Определение. Числовой последовательностью называется занумеро-

ванное множество чисел, расположенных в порядке возрастания их номеров: u1 , u2 , …, un , …,

u1 , u2 , … – элементы последовательности;

un – общий член последовательности: выражение для un – формула для вычисления любого члена последовательности.

Впоследовательности (1) un = 2n .

Вматематике различают постоянные и переменные величины. Пере-

менные величины, в свою очередь, бывают дискретными и непрерывными.

Пример 1.

tg x – непрерывная величина; выражение (3.1) – дискретная величина.

Определение.

Переменная величина

y называется ограниченной,

ес-

ли существует число C > 0 , что для всех своих значений

≤ C . В против-

ном случае величина y называется неограниченной.

Пример 2.

Рассмотрим

функцию

y = tg x

(рис. 3.13).

Если

;

, то

функция

−

x −

ограниченная, т.к.

≤ C =1.

−

O π

Если

;

, то

функция

x −

неограниченная.

Рис. 3.13

Определение.

Бесконечно малой (б/м) называется переменная вели-

чина α , которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любой, наперед заданной сколь угодно малой положительной величины ε : α → 0.

Пример 3.

α : 12 , 13 , …, 1n , …

0 – единственное б/м постоянное число.

Определение. Бесконечно большой (б/б) называется переменная величина β , которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается больше любого, наперед заданного сколь угодно большого положительного числа N : β → ∞.

§ 5. Понятие о пределе переменной

Рассмотрим переменную величину x , которая изменяется следующим образом:

x : 3,1; 3,01; 3,001; … 2,9 ; 2,99 ; 2,999 ; …

При последовательном изменении значение x приближается к значению 3 :

x −3 : 0,1; 0,01; 0,001; …

В этом случае говорят, что величина x → 3 : x → 3 lim x = 3.

Определение.

Постоянная величина a называется пределом перемен-

ной x , если разность x − a есть б/м величина, т.е.

lim x = a

x − a =α – б/м величина.

§ 6. Окрестность точки

Определение 1.

Окрестностью точки x0 радиуса ε (ε > 0 ) называет-

ся множество всех действительных чисел x таких, что

x − x0

< ε

(рис. 3.14).

Определение 2.

Проколотой

окрестностью точки

радиуса

(ε > 0 ) называется множество всех

действительных

чисел

таких,

что

0 <

x − x0

< ε (рис. 3.15).

Обозначения:

Oε (x0 ) – ε -окрестность точки x0 ;

(x ) – проколотая ε -окрестность точки x .

x −ε

x0 +ε

x0 −ε

x +ε

)

(

)

окрестность точки x0

проколотая окрестность точки x0

Рис. 3.14

Рис. 3.15

§ 7.

Предел функции в точке

Пусть дана функция

f (x) ,

определенная в проколотой окрестности

точки x0 .

Определение 1.

Число b называется пределом функции f (x) в точке

x0 (при x → x0 ), если для любого сколь угодно малого числа ε > 0 существу-

ет δε > 0		такое,	что для всех x ,	удовлетворяющих соотношению
0 <	x − x0	<δε , выполняется неравенство		f (x) −b	< ε .
0 <	x − x0	<δε , выполняется неравенство		f (x) −b	< ε .
	Обозначение:		lim f (x) = b .
			x→x0

Геометрический смысл предела

f (x)

b +ε

b b −ε

O	x0	−δε x0 x0		+δε x

Рис. 3.16

Пример 1.

Доказать:

lim(3x +1) = 7 .

x→2

Доказательство.

Для любого ε > 0 имеем:

f (x) −7

< ε

3x +1−7

3x −6

= 3

x − 2

< ε

x − 2

< ε =δε .

Таким образом, для любого

ε > 0

существует δε

такое, что как

x − 2

f (x) −7

только

<δε

< ε . Следовательно, lim(3x +1) = 7 .

x→2

Определение 2.

Число

называется

пределом

функции

f (x) при

x → +∞, если для любого сколь угодно малого числа ε > 0

существует такое

Nε , что для всех x > Nε выполняется неравенство

f (x) −b

< ε .

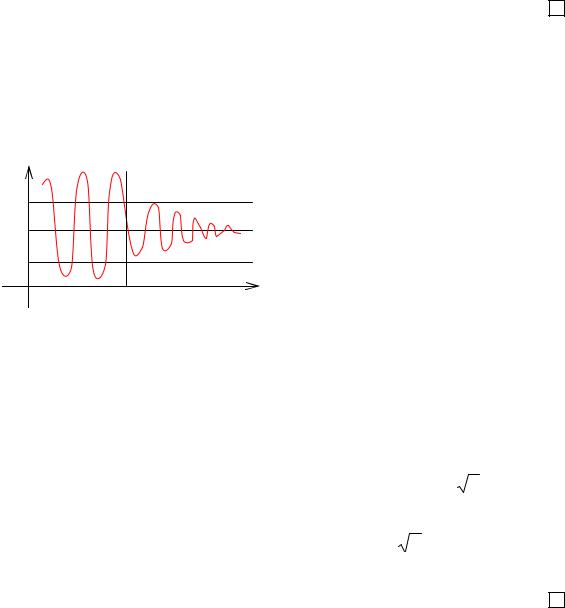
Геометрический смысл предела

f (x)

b −ε

b +ε

Nε

Рис. 3.17

Пример 2.

Доказать:

lim

x2 +sin x

=1.

x→+∞

Доказательство. Для любого ε > 0 имеем:

f (x) −1

+sin x

−1

sin x

< ε

= Nε

Nε =

Тогда для любого ε > 0 существует такое

что как только

x > Nε

f (x) −1

< ε . Следовательно, lim

+sin x

=1.

x→+∞

§ 8.

Односторонние пределы функции в точке

Определение 1.

Число

называется

пределом

функции

f (x) при

x → x0

слева, если для любого сколь угодно малого числа ε > 0

существует

такое

δε

> 0 ,

что

для

всех

x ,

удовлетворяющих

соотношению

x0 −δε

< x < x0 , выполняется неравенство

f (x) −b1

< ε .

Обозначение:

lim

f (x) = b1 .

x→x0 −0

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 3724 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
27.05.20193.56 Mб250КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf
#
27.05.20191.54 Mб178КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf
#
27.05.201920.05 Mб9037Письменный Д.Т. Конспект лекций по высшей математике - Полный курс.pdf