33
Формула (5) дает разложение вектора a по прямоугольному Декартову базису. Числа ax , ay , az называют при этом прямоугольными или Декартовыми
координатами вектора ar.
Из теорем о проекциях следует, что линейные операции над векторами можно заменить арифметическими действиями над их Декартовыми коорди-
натами. |
ar = ax ir + ay j + az k , |
b = bx i + by j + bz kr. |
||||||||||||
Пусть |
||||||||||||||
Тогда |
|
λ ar = λax i + λay j + λaz k , |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
ar ± br = (a |
x |
± b ) i |
+ (a |
y |
± b |
y |
) j |
+ (a |
z |
± b |
) kr. |
|
|
|
|
|
x |
|
|
|
|
|
z |
||||
Пример. |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
r |
|
|
|
|
|
|
|
|
|
|
|
||
a |
= 5i |
−10 j + 3k , b = −4i + 2 j −8k . |
|
|
|
|
||||||||
Тогда 3ar + 2b = (3 5 + 2 (− 4)) i + (3 (−10)+ 2 2) j + (3 3 + 2 (−8)) k = = 7ir − 26 rj − 7k .
Зная координаты вектора a , можно легко найти выражение для модуля вектора ar.
На основании известной теоремы о длине диагонали прямоугольного параллелепипеда можно написать:
→ |
|
2 |
|
→ |
|
2 |
|
→ |
|
2 |
|
→ |
|
2 |
ar |
|
2 = ax2 + a2y + az2 |
|
|
|
|
|
|
|
|||||||||||
OM |
|
= |
|
OM1 |
|
+ |
|
OM 2 |
|
+ |
|
OM 3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ar = 
ax2 + a2y + az2 .
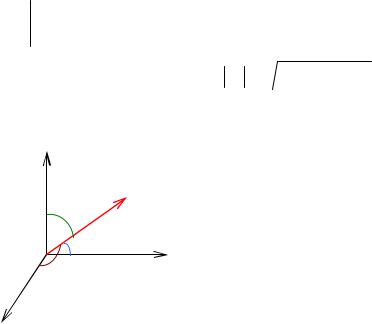
7.3Направляющие косинусы вектора
|
z |
|
Пусть вектор a образует с координатны- |
|||||||||||||
|
|
|
ми осями Ox , Oy и Oz углы α , β , γ соответ- |
|||||||||||||
|
γ a |
|
ственно (рис. 1.15). Эти три угла однозначно |
|||||||||||||
|
β |
|
определяют направление вектора ar |
в простран- |
||||||||||||
O |
y |
стве, поэтому косинусы этих углов cosα , cos β , |
||||||||||||||
α |
cosγ называют направляющими |
косинусами |
||||||||||||||
|
|
|
вектора a . |
|
ar = ax i + ay rj + az kr. Тогда из |
|||||||||||
x |
Рис. 1.15 |
|
Пусть |
|
||||||||||||
|
теоремы 1 о проекциях |
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
ax = прOxa = |
|
|
|
a |
|
|
cosα , |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
ay = прOy a = |
|
|
|
|
a |
|
|
|
cos β , |
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
az = прOza = |
|
|
a |
|
cosγ . |
|
|||||||
|
|
|
|
|
|
|||||||||||
34
Отсюда:
cosα = |
|
ax |
|
= |
|
ax |
|
|
, |
cos β = |
|
|
ay |
|
= |
ay |
, |
||||
|
ar |
|
|
|
|
|
|
|
ar |
|
|
||||||||||
|
|
ax2 + a2y |
+ az2 |
|
|
|
ax2 + a2y + az2 |
||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cosγ = |
|
|
az |
|
= |
|
az |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
ar |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ax2 + a2y |
+ az2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
cos2 α + cos2 β + cos2 γ =1. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||||||
Соотношение (6) является необходимым и достаточным условием для того, чтобы cosα , cos β , cosγ являлись направляющими для некоторого вектора пространства.
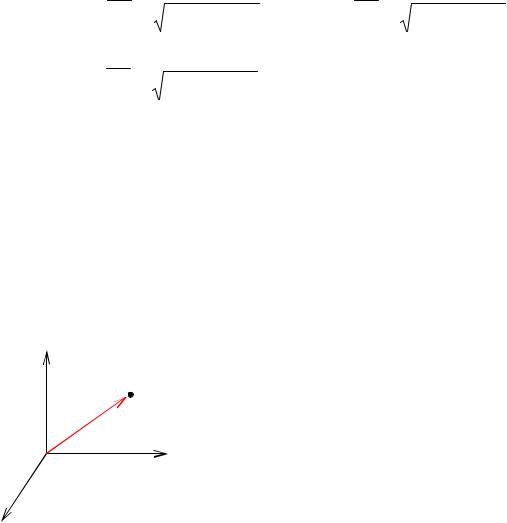
7.4 Радиус-вектор
Пусть в пространстве задана прямоугольная Декартова система координат Oxyz . Тогда любая точка пространства
|
z |
M однозначно определяется тремя числами |
||||||||||
|
M |
x , |
y , |
|
z , |
которые равны соответствующим |
||||||
|
|
|
|
|
|
|
|
|
|
→ |
||
|
|
координатам вектора OM (рис 1.16). |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
→ |
|
O |
|
|
|
|
|
Вектор OM называют радиус-вектором |
||||||
y |
точки M , а числа x , y , z – прямоугольными |
|||||||||||
|
||||||||||||
|
|
Декартовыми координатами точки M и пи- |
||||||||||
x |
|
шут M (x ; y ; z) . |
||||||||||
Рис. 1.16 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
7.5 Условие коллинеарности двух векторов |
|||||||||||
Пусть векторы ar и b |
коллинеарны. Тогда ar = λ br, т.е. ax = λ bx , |
|||||||||||
ay = λ by , az = λ bz , или |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a |
x |
= |
ay |
|
= |
a |
z . |
||
|
|
|
b |
x |
b |
y |
|
b |
||||
|
|
|
|
|
|
|
|
z |
||||
7.6 Простейшие задачи
Задача 1. Даны две точки M1(x1; y1; z1 ) и M 2 (x2 ; y2 ; z2 ) . Найти расстояние ρ (M1; M 2 ) между данными точками.
|
|
→ |
→ |
→ |
→ |
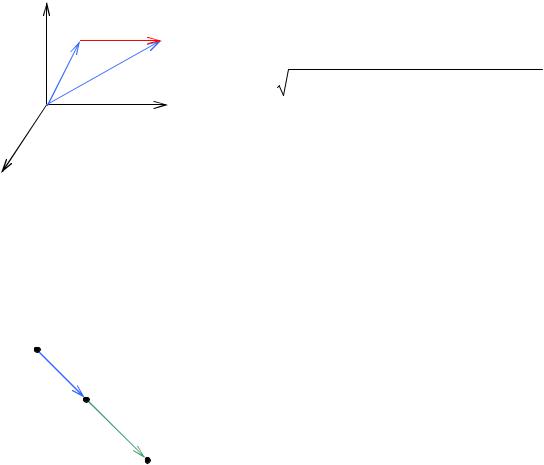
Решение. Построим |
вектор M1M 2 . Очевидно, |
M1M 2 |
= OM 2 |
−OM1 |
|
|
→ |
= {x2 − x1 ; y2 − y1 ; z2 − z1 |
}. |
|
|
(рис. 1.17). Тогда |
M1M 2 |
|
|
||
35
|
|
z |
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
M1 |
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
M 2 |
|
|
|
M1M 2 |
|
= ρ (M1; M 2 ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= (x |
2 |
− x )2 + ( y |
2 |
|
− y )2 |
+ (z |
2 |
− z )2 . |
|
|
|
||||||||||||
|
O |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Определение. |
Пусть |
дан |
|
отрезок |
|
|
AB , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
точка |
|
M , лежащая на данном отрезке и число |
|||||||||||||||||||||||
x |
|
Рис. 1.17 |
λ ≠ 0 . Если имеет место соотношение |
|
|
|
AM |
|
|
= λ , |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
MB |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то говорят, что точка M делит отрезок AB в отношении λ . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Задача 2. |
Даны две точки |
|
A(xA; yA; zA ) , |
B(xB ; yB ; zB ) |
|
и число λ ≠ 0 . |
||||||||||||||||||||||||||
Найти координаты точки M , делящей отрезок AB в отношении λ . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
A |
|
|
Решение. |
Обозначим искомые координаты точки |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M через x , y , |
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
→ |
|||||||||
|
|
|
|
|
|
M |
|
|
z . Построим векторы AM и MB |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(рис. 1.18). Тогда |
координаты |
этих |
|
|
векторов |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(задача 1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
= {x − xA; y − yA; z − zA}, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
B |
|
|
|
|
AM |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
− z }. |
|
|
|
|
|
|
|
|||
|
|
Рис. 1.18 |
|
|
|
|
MB = {xB − x ; yB − y ; zB |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
AM |
|
|
|
|
|
→ |
|
→ |
|
|
|
|
|
|
|
|
|
→ |
|
→ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Т.к. |
|
|
|
= λ и векторы AM и MB сонаправлены, то AM = |
λ MB . Отсюда |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
MB |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получаем соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x − xA = λ (xB − x) , |
|
y − yA = λ ( yB − y) , |
|
z − zA = λ (zB − z) . |
|
|
|
|||||||||||||||||||||||||
Тогда искомые координаты точки M равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x = |
xA + λxB |
, y = |
yA + λyB |
, |
z = |
zA + λzB |
. |
|
|
|
|
|
|
|
(7) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 + λ |
|
|
|
|
1 + λ |
|
|
|
|
|
1 + λ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полученные формулы (7) называются формулами деления отрезка в данном отношении.
Замечание 1. Если точка M – середина отрезка AB , то λ =1 и формулы (7) принимают вид
x = |
xA + xB |
, |
y = |
yA + yB |
, |
z = |
zA + zB |
. |
|
2 |
|
||||||
2 |
|
|
|
2 |
|
|||
Замечание 2. Прямоугольный Декартов базис и соответствующая ей прямоугольная система координат на плоскости вводятся аналогичным образом.
––––––––––––––––––––––––––––––––––
© Тимофеев В.А., Тимофеев А.А., 2008