Добавил:

sutkowska92 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Бухарский инженерно-технологический институт

Предмет:

Высшая математика

Файл:

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf

Скачиваний:

276

Добавлен:

27.05.2019

Размер:

3.56 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3721 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Пусть tgα =1,				α = 45o . Тогда:
5x′2 +5 y′2 + ( y′2 − x′2 ) 3 −32 = 0 , 2x′2 +8 y′2 = 32 ,
	x′2	+	y′2	=1 – уравнение эллипса.
16			4

Утверждение. Любое преобразование координат на плоскости можно свести к последовательному выполнению какого-либо параллельного переноса осей координат и поворота осей координат на некоторый угол α .

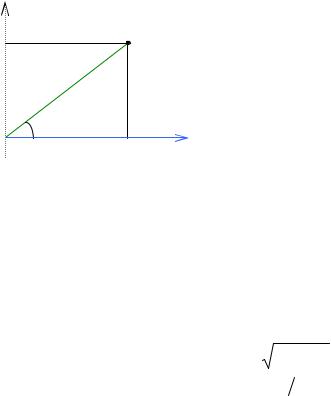
§ 7. Полярная система координат на плоскости

Наряду с Декартовой на плоскости используется полярная система координат, которая состоит из точки O (начала отсчета), называемой полюсом и одной оси, которая представляет собой луч Ox , этот луч называется поляр-

ной осью (рис. 2.22).

y				Тогда любую точку плоскости можно опи-
		M (ρ; ϕ)		сать с помощью двух чисел (ρ ; ϕ) , кото-
B		M (ρ; ϕ)		рые называются полярными координата-
B				рые называются полярными координата-
				ми:
				ρ – расстояние от точки O до точки M ,
	ϕ			ϕ – XOM .
	ϕ			ϕ > 0 , если Ox нужно поворачивать про-
			x
O		A
O		A		тив часовой стрелки,
	Рис. 2.22			тив часовой стрелки,
	Рис. 2.22			ϕ < 0 , если по часовой стрелке.

Если полюс полярной СК совпадает с началом ДСК, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат к декартовым координатам той же точки осуществляется по формулам:

x = ρ cosα,					(1)
y = ρ sin α.					(1)
y = ρ sin α.
В этом же случае формулы
		2		2
	x		+ y ,		(2)
ρ =	x		+ y ,		(2)
			x.
tgϕ = y			x.

являются формулами перехода от декартовых координат к полярным.

Пример.

x2 + y2 = r2 – уравнение окружности радиуса r с центром в начале ко-

ординат в ДСК.

Получим уравнение этой окружности в полярной СК:

ρ2 (cos2 ϕ +sin2 ϕ) = r2 , ρ2 = r2 ,

ρ = r – уравнение окружности в полярной СК.

––––––––––––––––––––––––––––––––––

§ 8. Поверхности второго порядка. Метод параллельных сечений

Определение. Поверхностями второго порядка называются поверх-

ности, которые описываются алгебраическими уравнениями второй степени относительно текущих координат x , y , z .

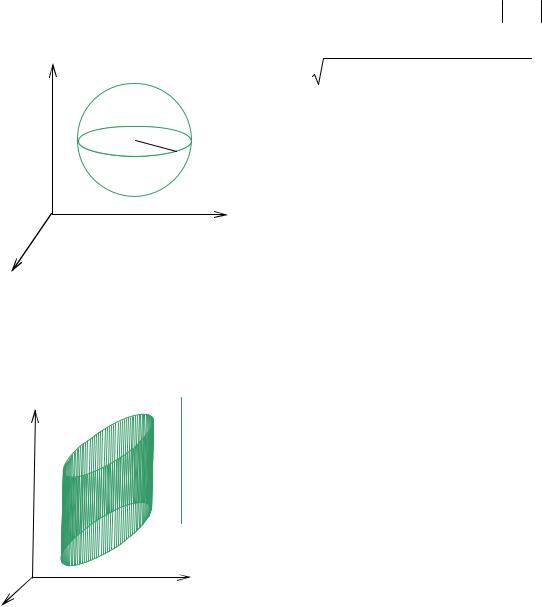
8.1 Сфера

Определение. Сферой называется множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы.

Пусть точка C(a; b; c) является центром сферы радиуса R (рис. 2.23). Возьмем произвольную точку M (x; y ; z) , лежащую на сфере, CM = R , тогда

C R

(x − a)2 + ( y −b)2 + (z −c)2 = R ,

(x − a)2 + ( y −b)2 + (z −c)2 = R2 . (1)

Уравнение (1) называется каноническим уравнением сферы с центром в точке C(a; b; c) радиуса R .

O	y	Если центр сферы совпадает с на-
		чалом координат, то уравнение (1) при-
x		мет вид
		x2 + y2 + z2 = R2 .	(2)
Рис. 2.23

8.2	Цилиндрические поверхности

Определение.

Рис. 2.24

Пример 1.

Пусть дана некоторая кривая L и прямая линия l

(рис. 2.24). Тогда цилиндрической поверхно-

lстью называется поверхность, состоящая из всевозможных прямых, параллельных прямой l и пересекающих кривую L . Кривая L называется направляющей линией цилиндрической поверхности, а прямые, из которых состоит поверхность, образующими.

Будем рассматривать только те цилиндрические поверхности, образующие кото-

yрых перпендикулярны одной из координатных плоскостей, а направляющие должны лежать в этой координатной плоскости.

Провести исследование поверхности x2 + y2 = r2 .

zРешение. Отсутствие одной из координат говорит о том, что это цилиндрическая поверх-

ность. Применим метод параллельных сече-

ний.

Рассмотрим сечение плоскостью z = 0 :

получим уравнение x2 + y2 = r2

– урав-

нение окружности.

Рассмотрим сечение плоскостью z = a :

получим уравнение x2 + y2 = r2

– урав-

нение окружности.

Таким образом, данная поверхность пред-

Рис. 2.25

ставляет собой круговой цилиндр (рис. 2.25).

Пример 2.

Провести исследование поверхности x2 = z .

Решение. 1) Рассмотрим сечение плоскостью

y = 0 : в плоскости

XOZ получим уравнение

x2 = z – уравнение параболы.

2) Рассмотрим сечение плоскостью y = a : по-

a y

лучим уравнение x2 = z – уравнение парабо-

лы.

Таким образом, данная поверхность пред-

ставляет собой

параболический

цилиндр

Рис. 2.26

(рис. 2.26).

8.3

Конические поверхности

Определение.

Поверхность,

составленная

из всех прямых,

пересе-

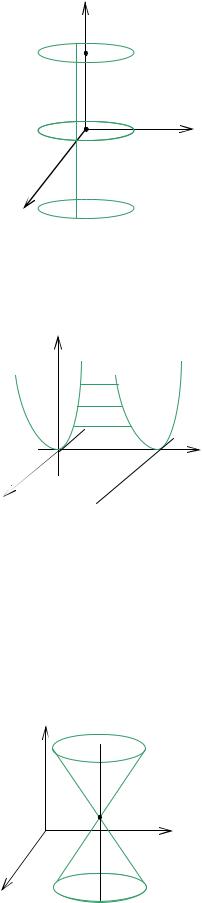
кающих данную линию L и проходящих через данную точку P , называется

конической поверхностью (рис. 2.27). Кривая L называется направляющей

конической поверхности, точка P – ее вершиной,

а каждая из прямых, со-

ставляющих коническую поверхность – образующей.

Уравнение конуса второго порядка с вер-

шиной в начале координат, осью которого слу-

жит ось Oz , записывается в виде

−

= 0 .

(3)

Аналогично:

−

= 0 – уравнение конуса

второго

порядка, ось – Oy ;

= 0 – уравнение конуса второго

Рис. 2.27

−

порядка, ось – Ox ;

Пример 3.

Провести исследование поверхности 2x2 + y2 −3z2 = 0 .

Решение. 1) Рассмотрим сечение плоскостью z = 0

(плоскость XOY ): полу-

чим уравнение

2x2 + y2 = 0 .

Этому

уравнению

удовлетворяет

точка

O(0; 0) .

2) Рассмотрим сечение плоскостью

z = a : по-

лучим уравнение

+ y

= 3a

, или

=1 –

3a2 2

3a2

уравнение эллипса.

y = 0

Рассмотрим

сечение плоскостью

Рис. 2.28

(плоскость XOZ ): получим уравнение

2x2 = 3z2 .

Это уравнение пары прямых

z =

2 x и z = −

2 x .

4) Рассмотрим сечение плоскостью x = 0

(плоскость YOZ ): получим уравне-

ние

y2 = 3z2 .

Это уравнение пары прямых

y =

y = −

3z .

Таким образом, данная поверхность представляет

конус второго порядка

(рис. 2.28).

8.4

Поверхность вращения

Пусть линия L , лежащая в плоскости YOZ , задана уравнениями

F(Y; Z ) = 0,

(4)

X = 0.

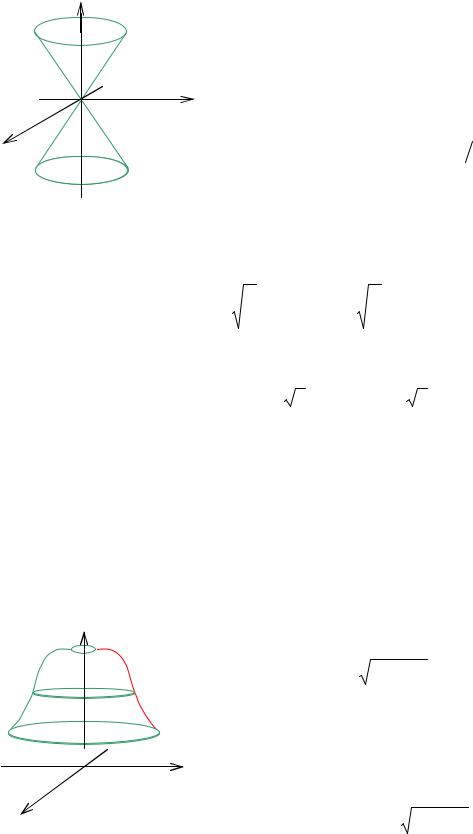
Рассмотрим поверхность, образованную вращением этой линии отно-

сительно оси Oz (рис.2.29). Уравнение этой по-

верхности:

F(±

x2 + y2 ; z) = 0 .

(5)

Уравнение (5) называется уравнением поверхно-

сти вращения относительно оси Oz линии L .

Это уравнение получается из первого уравнения

(4) заменой в нем координат Y

и Z

координа-

тами x ,

y , z

по формулам:

Y = ±

x2 + y2 ,

Рис. 2.29

Z = z .

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3721 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
27.05.20193.56 Mб276КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч1.pdf
#
27.05.20191.54 Mб211КРАТКИЙ КУРС ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ. Ч2.pdf
#
27.05.201920.05 Mб9395Письменный Д.Т. Конспект лекций по высшей математике - Полный курс.pdf

§ 7. Полярная система координат на плоскости

8.1 Сфера

Цилиндрические поверхности

Конические поверхности

Поверхность вращения