3 Скорость и ускорение точек, вращающегося тела

Выберем произвольную точку М твер­дого тела ( ), вращающегося вокруг неподвижной оси OZ (рис. 10.5). Движение точки М можно описать радиусом-век­тором , который имеет постоянный мо­дуль для выбранной точки:

. (10.5)

Дифференцируя (10.5) по времени, нахо­дим скорость:

, (10.6)

Рис. 10.5

где , так как вектор постоянен по величине и направлению как производная вектора постоянного модуля по скалярному аргументу.

Тогда

, (10.7)

где

. (10.8)

(h — расстояние от точки до оси вращения).

Вектор скорости будет направлен по касательной к траекто­рии точки М в соответствии с направлением угловой скорости.

Пример 4. Точка А, лежащая на ободе диска, имеет скорость = 40 см/с. Точка В, принадлежащая диску, имеет скорость = 10 см/с (рис. 10.6). Определить угловую скорость диска и его радиус, если расстояние АВ = 15 см.

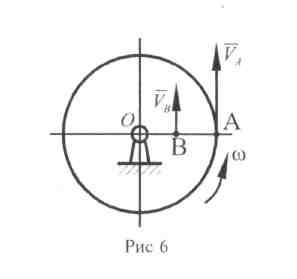
Рис. 10.6

Решение. Применим формулу (8)

,

.

Тогда

,

пли

,

откуда

,

,

см,

рад/с.

Ответ. R=20 см, ω=2 рад/с.

Получим векторную формулу Эйлера для скорости любой точ­ки твердого тела, вращающегося вокруг неподвижной оси. Из рис. 10.5 видно, что . Тогда . Это выра­жение является модулем векторного произведения , т.е. . Направление вектора скорости определяется век­торным произведением. Следовательно:

. (10.9)

Это выражение называют векторной формулой Эйлера.

Скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости на радиус-вектор этой точки, проведенный из произвольной точки на оси вращения.

Определим ускорение точки М:

,

так как

,

то

. (10.10)

Рассмотрим слагаемые, входящие в это выражение. Вектор в соответствии с правилом векторного произведения направлен по касательной к траектории точки М, т. е. как касательное уско­рение точки М, которое во вращатель­ном движении называют вращательным ускорением (рис. 10.7):

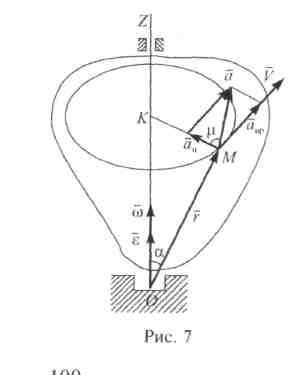
Рис. 10.7

. (10.11)

Величина вращательного ускорения

,

. (10.12)

Вектор находится в плоскости окружности радиуса КМ = h, направлен от точки М к оси вращения и является нормальным ускорением точки М. При вращательном движении это ускорение называют центростремительным ускорением:

. (10.13)

Величина центростремительного ускорения:

,

где ,

. (10.14)

Модуль полного ускорения точки, вращающегося твердого тела

. (10.15)

Угол между полным ускорением и центростремительным равен:

. (10.16)

Выражения (10.8) и (10.15) показывают, что скорости и ускорения точек вращающегося твердого тела пропорциональны расстояни­ям от этих точек до оси вращения, а из формулы (10.16) следует, что угол отклонения полного ускорения от центростремительно­го в каждый момент времени один и тот же для всех точек тела.

Уравнение равномерного вращения тела. Вращение тела с постоянной угловой скоростью называется равномерным. Составим уравнение равномерного вращения тела с угловой скоростью ω, принимая направление этого вращения за положительное направление отсчета угла поворота φ.

Положим, что в начальный момент t_o=0 угол поворота имеет значение φ₀. Тогда

.

Проинтегрируем уравнение в пределах, соответствующих начальному моменту t₀ = 0 и произвольному моменту времени t:

,

откуда

(10.17)

Выражение (10.17) является уравнением равномерного вращения тела. Если в начальный момент времени подвижная полуплоскость Q совпадает с неподвижной полуплоскостью Р, т. е. φ₀ = 0, то уравнение равномерного вращения тела (10.17) принимает вид

Из уравнения равномерного вращения тела при

,

т. е. угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к этому промежутку времени.

Число оборотов, совершаемых вращающимся телом за единицу вре­мени (обычно за минуту), называется частотой вращения и обозна­чается n. Так как один оборот равен 2π радиан, то зависимость между угловой скоростью ω (рад/с) и частотой вращения n (об/мин) имеет вид

, .

Уравнение равнопеременного вращения тела. Вращение тела, при кото­ром угловое ускорение постоянно, называют равнопеременным враще­нием. При этом, если абсолютная величина угловой скорости увеличи­вается, вращение называют равноускоренным, и если уменьшается - равнозамедленным.

Составим уравнение равнопеременного вращения, полагая, что в начальный момент t₀ = 0 начальная угловая скорость , а начальное значение угла поворота φ₀. Тогда

.

Проинтегрируем уравнение в пределах, соответствующих началь­ному моменту t₀=0 н произвольному моменту времени t:

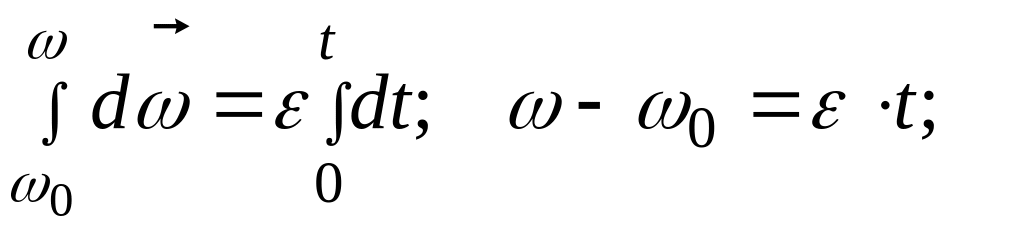
, (10.18)

.

Проинтегрируем это уравнение в соответствующих пределах:

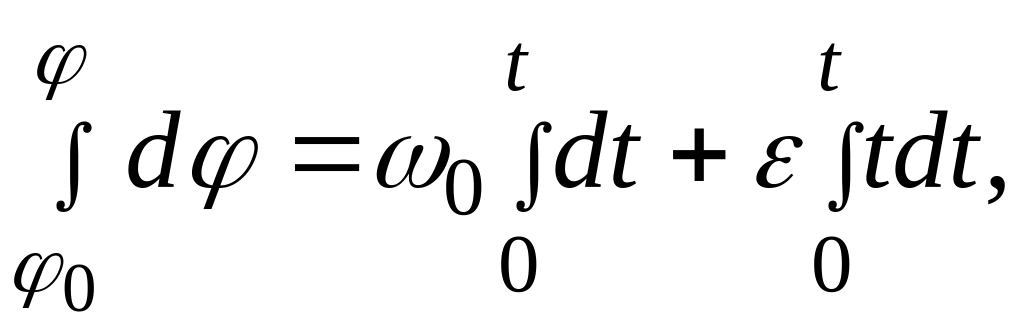
. (10.19)

Уравнение (10.19) является уравнением равнопеременного вращения тела.

Так как равнопеременное вращение происходит обычно в одном направлении, то где знак плюс соответствует уско­ренному вращению, а знак минус - замедленному. Учитывая это, формулам (18) и (19 можно придать более удобный для решения задач вид:

.

Из формулы угловой скорости находим , т. е. при равно­переменном вращении абсолютное значение углового ускорения тела равно отношению изменения угловой скорости тела за некоторый промежуток времени к числовой величине этого промежутка.

Пример 5. Вал начинает вращаться равноускоренно из состояния покоя; в первые 20 с он совершает 100 оборотов. Каковы его угловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покое, то ω₀=0. В этом случае при φ₀=0

, (1)

(2)

Из уравнения (1) находим

, (3)

где .

Подставляя в (3) числовые значения, находим