Аналитическая форма

Равнодействующая сходящихся сил (рис. 2.11) равна геометрической сумме этих сил:

.

Рис. 2.11

Проекция равнодействующей на каждую из координатных осей равна алгебраической сумме проекций всех составляющих:

(2.8)

здесь проекции сил вычисляются по формулам:

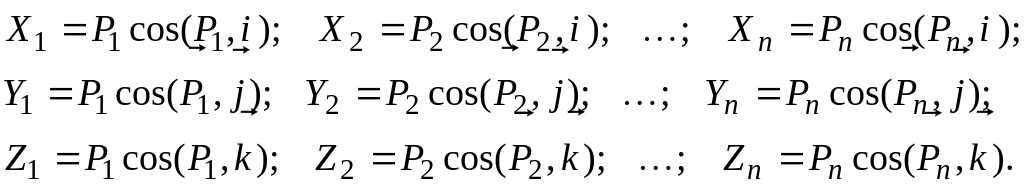
Формулам (3) можно придать вид

(2.9)

причем i=1,2,…,n.

Вычислив проекции равнодействующей X, У и Z, найдем модуль и направление равнодействующей по формулам (2.8) и (2.9):

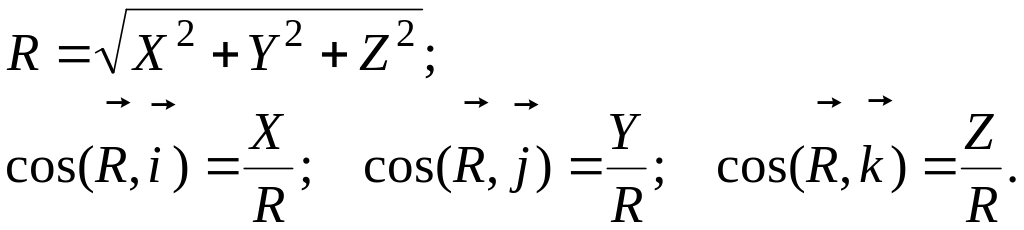
В случае если силы взаимно уравновешиваются, их равнодействующая равна нулю. Так как

.

Таким образом, для сходящихся сил в пространстве имеем следующие три уравнения равновесия:

(2.10)

При помощи уравнений (2.10) можно решать задачи на равновесие сходящихся сил, если число неизвестных в задаче не превышает трех. Такой метод решения этих задач называется аналитическим.

Для сходящихся сил, расположенных в одной плоскости, получаем два уравнения равновесия:

. (2.11)

При помощи этих уравнений можно решить задачу на равновесие сходящихся сил на плоскости, если число неизвестных в ней равно двум.

Если в задаче на равновесие сходящихся сил число неизвестных превышает число уравнений равновесия, то ее нельзя решить методами статики твердого тела.

4. Теорема о трех непараллельных силах

Линии действия трех непараллельных взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке.

Пусть к твердому телу в точках приложены три непараллельные взаимно уравновешивающиеся силы , лежащие в одной плоскости (рас. 2.12). Перенесем силы и в точку О пересечения линий их действия и найдем равнодействующую , которая будет приложена в этой же точке.

Рис. 2.12

Сила , будучи уравновешивающей системы сил и , равна по модулю их равнодействующей и направлена по линии ее действия в противоположную сторону.

Следовательно, линия действия силы , проходит через точку О, что и требовалось доказать.

Три силы, не лежащие в одной плоскости, уравновешиваться не могут.

Задача 1. Груз весом удерживается в равновесии на гладкой наклонной плоскости посредством параллельного ей троса. Определить давление груза на плоскость и силу реакции троса, если наклонная плоскость образует угол α с горизонтом. Груз считать материальной точкой (рис. 2.13).

Решение. Графический способ. Рассмотрим равновесие груза. Задаваемой силой является вес груза направленный по вертикали вниз. Силы реакций связей: - реакция троса направлена вдоль троса вверх; - реакция наклонной плоскости направлена по нормали вверх.

Строим силовой треугольник начиная с силы , известной как по величине, так и по направлению. Выбрав произвольную точку О вне основного рисунка, изображаем силу . Затем к концу силы прикладываем силу , для чего проведем прямую AD, параллельную линии действия силы . На этой прямой откладываем силу . К концу силы прикладываем начало силы . Так как треугольник должен быть замкнутым, то конец силы должен совпадать с началом О силы .

Рис. 2.13

Угол ОАВ равен углу α, так как их стороны взаимно перпендикулярны, а угол АВО является прямым, так как линии действия сил и взаимно перпендикулярны. Из треугольника ОАВ находим:

.

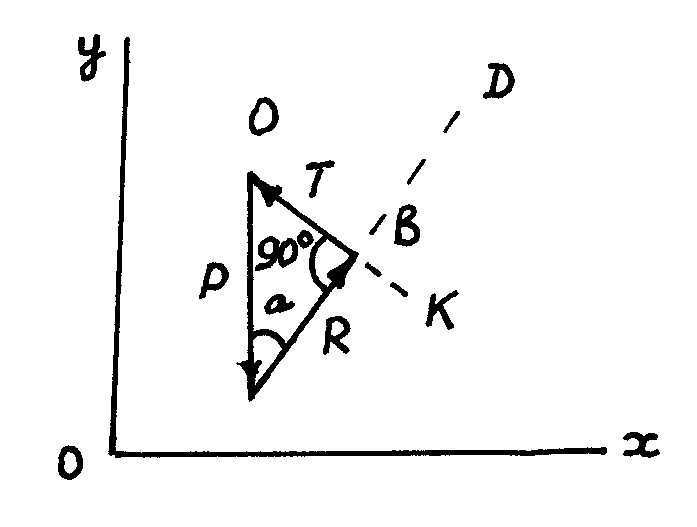
Рис. 2.14

Аналитический способ. Направим ось х по горизонтали направо и ось у по вертикали вверх (рис. 2.14). Составим уравнения равновесия груза в проекциях на оси х и у:

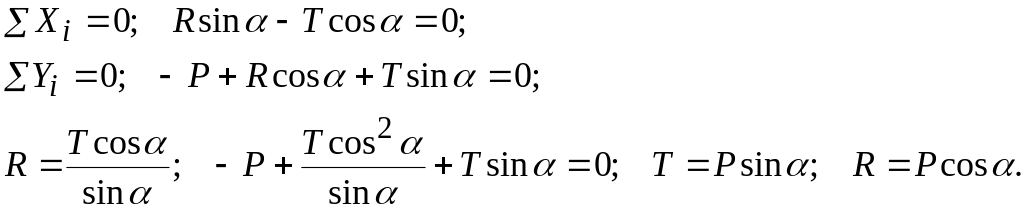
Задача 2. Груз M₁ весом Р (рис. 1.2.1, а) подвешен на гибком не­растяжимом тросе ОМ₁ отклоненном от вертикали на угол α, и удерживается в равновесии при помощи другого гибкого нерастя­жимого троса М₁АМ₂, охватывающего идеальный блок А и несущего на свободном конце груз М₂. Считая, что при равновесии участок троса М₁А горизонтален, определить величину Q веса груза М₂ и на­тяжение троса ОМ₁. Размерами груза М₁ и весом тросов пренебречь.

Решение. Рассмотрим равновесие груза М₁. Задаваемыми сила­ми являются вертикально направленная сила Р и горизонтально на­правленная сила Т₂, равная по величине весу груза Q, так как иде­альный блок А изменяет только направление силы.

На груз М₁ наложена связь, осуществляемая тросом OM₁. Осво­бодим груз от связи. Реакция связи Т₁ направлена по тросу вверх. Таким образом, груз M₁ находится в равновесии под действием пло­ской сходящейся системы трех сил: Р, Т₁ и Т₂, причем T₂ = Q (рис. 1.2.1, б). Решим эту задачу двумя способами: геометрическим и аналитическим.

Рис. 1.2.1

Геометрический способ. Поскольку точка М₁ находится в рав­новесии под действием трех сил, то силовой треугольник, построен­ный на этих силах, должен быть замкнутым (рис. 1.2.1, в). Построение силового треугольника следует начинать с заданной силы Р. Изо­бразив вектор Р, проводим через его начало и конец прямые, парал­лельные направлениям сил Т₁ и Т₂. Точка пересечения этих прямых определит третью вершину силового треугольника. Ориентация всех векторов должна быть такова, чтобы силовой треугольник был замкнутым. Это дает возможность проверить правильность направ­ления неизвестных реакций.

Из силового треугольника находим

Таким образом, вес Q груза М₂, равный Т₂, будет Q = Ptgα, а натя­жение троса ОМ₁ численно равно

.

Аналитический способ. Выберем оси координат. Их следует вы­бирать так, чтобы уравнения равновесия имели простейший вид. Этого можно добиться, проводя оси перпендикулярно неизвестным силам. Проведем ось М₁у перпендикулярно неизвестной силе Т₂, а ось М₁x - горизонтально.

Система приложенных сил Р, T₁ и Т₂ - плоская сходящаяся сис­тема, для которой имеют место два уравнения равновесия. В задаче две неизвестные величины: Т₁ и Т₂, т.е. задача статически определима.

Составим уравнения равновесия:

Отсюда находим

.

Если воспользоваться осями М₁у и М₁у’, то получим

В каждое из этих уравнений входит только по одному неизвест­ному, что упрощает их нахождение.

Задача 3. Однородный цилиндр А весом Р и радиусом r (рис. 1.2.2, а) опирается на гладкую поверхность цилиндра В радиусом R и удерживается в равновесии при помощи нити CD длиной l, расположенной в поперечной плоскости симметрии. Определить натяжение нити и реакцию цилиндрической поверхности.

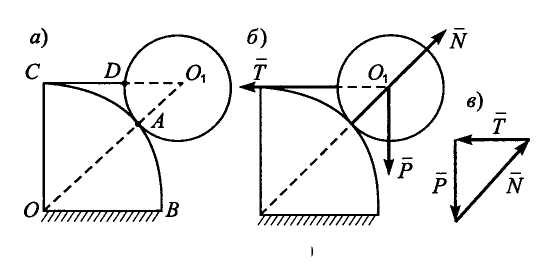
Рис. 1.2.2

Решение. Рассмотрим равновесие цилиндра А. На него действует сила Р, направленная вертикально вниз. Связями являются гладкая цилиндрическая поверхность В и нить CD. Освободимся от связей. Реакция N (рис. 1.2.2, б) цилиндрической поверхности направлена по общей нормали к цилиндрам и, следовательно, про­ходит через точку Ох. Реакция Т направлена по нити CD. Поскольку на цилиндр А действуют три силы, то на основании теоремы о трех силах их линии действия должны пересекаться в точке Ох. Следовательно, цилиндр А при равновесии займет такое положение, при котором нить CD будет являться продолжением его радиуса.

Построим силовой треугольник (рис. 1.2.2, в). Этот треугольник подобен ΔOO₁C. Из подобия треугольников имеем

или .

Отсюда находим

Задача 4. Прямоугольная пластина со сторонами АВ = а и ВС = b (рис. 1.2.3) шарнирно закреплена в вершине В, а вершиной А опирается на гладкую вертикальную стену ЕЕ. Пренебрегая весом пластины, определить реакции стены и шарнира, если к вершине С пластины подвешен груз М весом Р.

Рис. 1.2.3 Рис. 1.2.4

Решение. Рассмотрим равновесие пластины. Задаваемой силой является вес груза Р. Связями являются стена ЕЕ и шарнир В. Реакция N_A (рис. 1.2.4) гладкой стены направлена по нормали к стене, реакция R_B шарнира В заранее по направлению не определена. Поскольку пластина находится в равновесии под действием трех непараллельных сил Р, N_A, R_B, то на основании теоремы о трех силах заключаем, что линии действия этих сил должны пересекаться в одной точке К - точке пересечения линий действия сил Р и N_A. Тем самым вполне определяется линия действия реакции R_B. Для нахождения величин реакций следует использовать уравнения равновесия.

Решим задачу геометрическим способом. Составим силовой треугольник (рис. 1.2.5). Он должен быть замкнутым. Для построения сило­вого треугольника отложим от произвольной точки О вектор Р, из его начала О и конца L проведем прямые, параллельные линиям действия сил R_B и N_A.

Рис. 1.2.5

Пусть S - точка пересечения этих прямых. Тогда

.

Опустим из точки В перпендикуляр ВТ на прямую АК, получим

~ ,

следовательно,

или .

Из треугольника АВТ находим

,

где α - угол, составленный стороной АВ с горизонтом. Отрезок ТК является проекцией отрезка ВС, следовательно,

.

Далее,

.

Подставляя эти величины, имеем

отсюда

Задача 5. Груз весом Р = 60 кН подвешен при помощи каната, перекинутого через небольшой блок А и идущего к лебедке D. Определить усилия в стержнях АС и ВА крана. Углы, определяющие направления стержней и каната, заданы на рис. 1.2.6.

Решение. Рассмотрим равновесие узла А крана, к которому приложены сила Р, реакции стержней АС и АВ и сила натяжения каната AD. Обозна­чим реакцию стержня АВ через S₁ реакцию стержня АС через S₂ и силу натяжения каната AD через Т.

Реакции стержней S₁ и S₂ направим вдоль этих стержней от узла А; сила Т направлена, очевидно, вдоль каната от А к D, так как канат растянут. Кроме того, Т=Р, так как при отсутствии трения в блоке натяжение каната, перекинутого через этот блок, во всех точках одинаково.

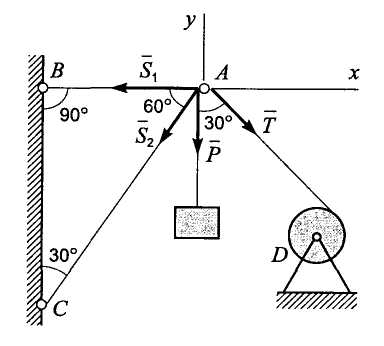
Рис. 1.2.6

Так как узел А находится в равновесии под действием сил S₁, S₂, P, Т, то можно составить два уравнения равновесия этой системы сходящихся сил.

Выберем оси координат, как указано на рис. 1.2.6, найдем проекцию каждой силы на эти оси и составим два уравнения равновесия, приравнивая нулю сумму проекций всех сил на каждую из координатных осей:

Из второго уравнения находим:

кН,

S₂ =-129,1 кН.

Теперь из первого уравнения получаем:

кН.

Так как полученное значение силы S₂ отрицательно, то сила S₂ имеет направление, противоположное направлению, выбранному на рисунке, т.е. она направлена от С к А, и, следовательно, стержень АС сжат.

Задачу можно решить и геометрически, построив замкнутый многоугольник сил Т, Р, S₁, S₂ (рис. 1.2.7).

Рис. 1.2.7

Направления сил S₁ и S₂ найдем после того, как обойдем периметр построенного силового многоугольника, причем направ­ление этого обхода определяется направлением известных сил Р и Т.

Измерив стороны cd и da силового многоугольника выбранной единицей масштаба, найдем величину искомых сил S₁ и S₂. Так как углы между силами Т, Р, S₁, S₂ заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон. В самом деле, из построения силового многоугольника следует, что

,

а потому

.

Если соединим точки а и с, то треугольник аbс будет равно­бедренным, так как Р = Т, а потому

.

Отсюда следует, что

.

Применяя теперь к треугольнику adc теорему синусов, получим:

,

откуда

,

.

Чтобы определить, будут ли стержни АВ и АС сжаты или растянуты (рис. 1.2.7), перенесем векторы S₁ и S₂ с силового многоугольника на стержни АВ и АС, тогда сила S₂ будет направлена к узлу А, а сила S₁, от узла А, а потому стержень АС сжат, а стержень АВ растянут.

Задача 6.. Жесткая рама (рис. 1.2.8) закреплена в точке А при помощи неподвижного цилиндрического шарнира, а в точке В опирается катками на гладкую наклонную плоскость, составляющую с горизонтом угол α = 30°. На горизонтальном участке CD рама находится под действием равномерно распределенной вертикаль­ной нагрузки интенсивности q = 5 кН/м. Определить реакции опор в точках А и В. если CD = 2a = 2,1 м и ОК = b = .

Рис. 1.2.8

Решение. Найдем сначала равнодействующую Q системы параллельных сил, приложенных к раме на участке CD, которая равна сумме слагаемых сил, т.е.

кН

и приложена в середине отрезка CD. Реакцию опоры В обозначим через R_B. Она направлена перпендикулярно к опорной плоскости катков. Реакция R_A неподвижного шарнира приложена к раме в точке А, но направление ее неизвестно. Для определения линии действия силы R_A воспользуемся теоремой о трех непараллельных силах. Так как рама находится в равновесии под действием трех сил Q, R_B и R_A, то линии действия этих сил пересекаются в одной точке.

Продолжив линии действия сил Q и R_B, найдем точку Е, через которую должна проходить сила R_A, приложенная в точке А. Следовательно, прямая АЕ является линией действия силы R_A. Теперь задача может быть решена двумя способами: геометрическим (построением замкнутого силового треугольника) и аналитическим (методом проекций). Построим замкнутый треугольник abc сил , и , в котором , а стороны bc и са соответственно параллельны прямым BE и АЕ. Тогда и (рис. 1.2.8, б). Далее определим углы в построенном силовом треугольнике: . Из прямоугольного треугольника КЕВ находим:

,

следовательно, ОЕ = КЕ – КO = , или ОЕ = = а. Отсюда АО = ОЕ и . В треугольнике abc проведем прямую се, перпендикулярную к ab, тогда ае = се =bс/2, be = bccos30°,

,

а потому

кН,

кН.

Рассмотрим теперь аналитический способ решения. Начало ко­ординат выберем в точке О, ось у направим по прямой ОЕ, а ось х — по прямой АО. Проектируя силы Q, R_A и R_B на оси х и у, получим следующие два уравнения равновесия:

Из первого уравнения находим

.

Тогда из второго уравнения имеем

Отсюда

Задача 7. По направлению стропильной ноги, наклоненной к горизонту под углом α = 45^о, действует сила Q=2,5 кН (рис. 1.2.9, а). Какое усилие S возникает при этом по направлению горизонтальной затяжки и какая сила N действует на стену по отвесному направлению?

Решение.

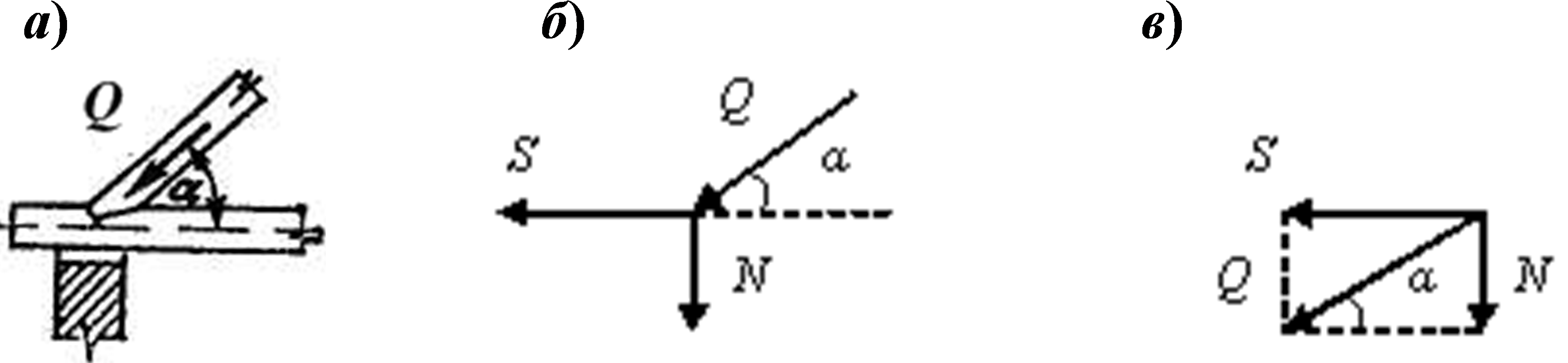
Рис. 1.2.9

1) выделим твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин: точка, где сходятся задаваемая сила Q и силы реакций связи (рис. 1.2.9, б);

2) изображаем задаваемую силу Q (рис. 1.2.9, б);

3) применив принцип освобождаемости от связей, приложим к твердому телу соответствующие силы реакций связей S и N (рис. 1.2.9, б);

4) рассмотрим равновесие данного несвободного твердого тела, находящегося под действием задаваемой силы Q и сил реакций связей S и N; построим замкнутый силовой многоугольник (построение следует начинать с силы, известной как по величине, так и по направлению) (рис. 1.2.9, в);

5) решив силовой многоугольник, определим искомые величины.

;

;

.

Задача 8. Стержни АС и ВС соединены между собой и с верти­кальной стеной посредством шарниров. На шарнирный болт С действует вертикальная сила Р = 1000 Н. Определить реакции этих стержней на шарнирный болт С, если углы, составляемые стержнями со стеной, равны: а = 30° и β=60° (рис. 1.2.10).

Решение.

Рис. 1.2.10

.

Задача 9. На железной дороге, проведенной в горах, участок пути в ущелье подвешен так как показано на чертеже. Предполагая подвеску АВ нагруженной силой Р = 500 кН, найти усилия в стержнях АС и AD (рис. 1.2.11).

Решение.

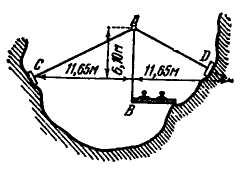
Рис. 1.2.11

Задача 10. Груз весом удерживается в равновесии на гладкой наклонной плоскости посредством параллельного ей троса. Определить давление груза на плоскость и силу реакции троса, если наклонная плоскость образует угол α с горизонтом. Груз считать материальной точкой (рис. 1.2.12).

Решение. Геометрический способ. Рассмотрим равновесие груза. Задаваемой силой является вес груза направленный по вертикали вниз. Силы реакций связей: - реакция троса направлена вдоль троса вверх; - реакция наклонной плоскости направлена по нормали вверх.

Строим силовой треугольник, начиная с силы , известной как по величине, так и по направлению. Выбрав произвольную точку О вне основного рисунка, изображаем силу . Затем к концу силы прикладываем силу , для чего проведем прямую AD, параллельную линии действия силы . На этой прямой откладываем силу . К концу силы прикладываем начало силы . Так как треугольник должен быть замкнутым, то конец силы должен совпадать с началом О силы .

Рис. 1.2.12

Нетрудно видеть, что угол ОАВ равен углу α, так как их стороны взаимно перпендикулярны, а угол АВО является прямым, так как линии действия сил и взаимно перпендикулярны. Из треугольника ОАВ находим:

.

Аналитический способ. Направим ось х по горизонтали направо и ось у по вертикали вверх. Составим уравнения равновесия груза в проекциях на оси х и у:

Задача 11.  Однородная балка длиной 2а, вес которой равен Р, прикреплена к полу шарниром А и опирается другим концом в точке В на выступ вертикальной стены. Определить силы реакций выступа В и шарнира, если балка образует угол 30⁰ с горизонтом (рис. 1.2.13, а).

Решение. Вес балки - задаваемая сила приложен в середине балки в точке С и направлен по вертикали вниз. На балку наложены две связи: выступ В и шарнир А. Сила опорной реакции выступа В направлена перпендикулярно к балке. Направление силы реакции шарнира А заранее неизвестно. Однако в данной задаче можно воспользоваться теоремой о трех непараллельных силах и указать направление действия силы реакции шарнира А. Действительно, проведя линии действия сил и (рис. 1.2.13, б), определим их точку пересечения О. Так как балка находится в равновесии под действием трех сил , и , то линия действия этих сил должна пересекаться в одной точке, т.е. линия действия силы реакции шарнира должна пройти через эту точку . Поэтому проводим линию действия силы реакции шарнира через ее точку приложения - шарнир А и точку О.

Рис. 1.2.13

Строим замкнутый силовой треугольник. Из точки D проводим силу . Через начало и конец силы проводим прямые DN и EK, соответственно параллельные линиям действия сил и (рис. 1.2.13, в).

В точке пересечения прямых DN и ЕК находим третью вершину М силового треугольника DEM. Направляем векторы сил так, чтобы в каждой из вершин силового треугольника был расположен конец одной из сил.

Нетрудно видеть, что силовой треугольник подобен ∆OCL, так как стороны их соответственно параллельны. Для определения модулей сил и вычислим длины сторон Δ OCL.

,

так как центр тяжести однородной балки расположен в ее середине.

Учитывая, что , как углы с взаимно перпендикулярными сторонами, из прямоугольного Δ ВОС находим, что

; .

Отрезок CL является средней линией Δ АОВ, и потому его длина равна половине основания треугольника, т.е.

.

Из прямоугольного Δ ОАВ получим

.

Наконец 

.

Итак, стороны Δ COL равны:

.

На основании подобия Δ DEM и Δ COL имеем:

,

откуда

.

  Задача 12.  К стержню АВ приложены непараллельные силы, лежащие в одной плоскости: сила тяжести и реакции опор и (рис. 1.2.14, a).

По теореме о трех непараллельных силах линии действия сил , , пересекаются в одной точке и, следовательно, образуют систему сходящихся сил. Реакция в опоре A направлена горизонтально и ее линия действия пересекается с линией действия силы в точке С . Через эту точку должна проходить и линия действия силы . Угол  β находим из условия:

При аналитическом решении проводим оси координат, указываем предполагаемые направления реакций опор и составляем уравнения равновесия в проекциях на оси координат:

.

;

.

Отсюда находим:  

;

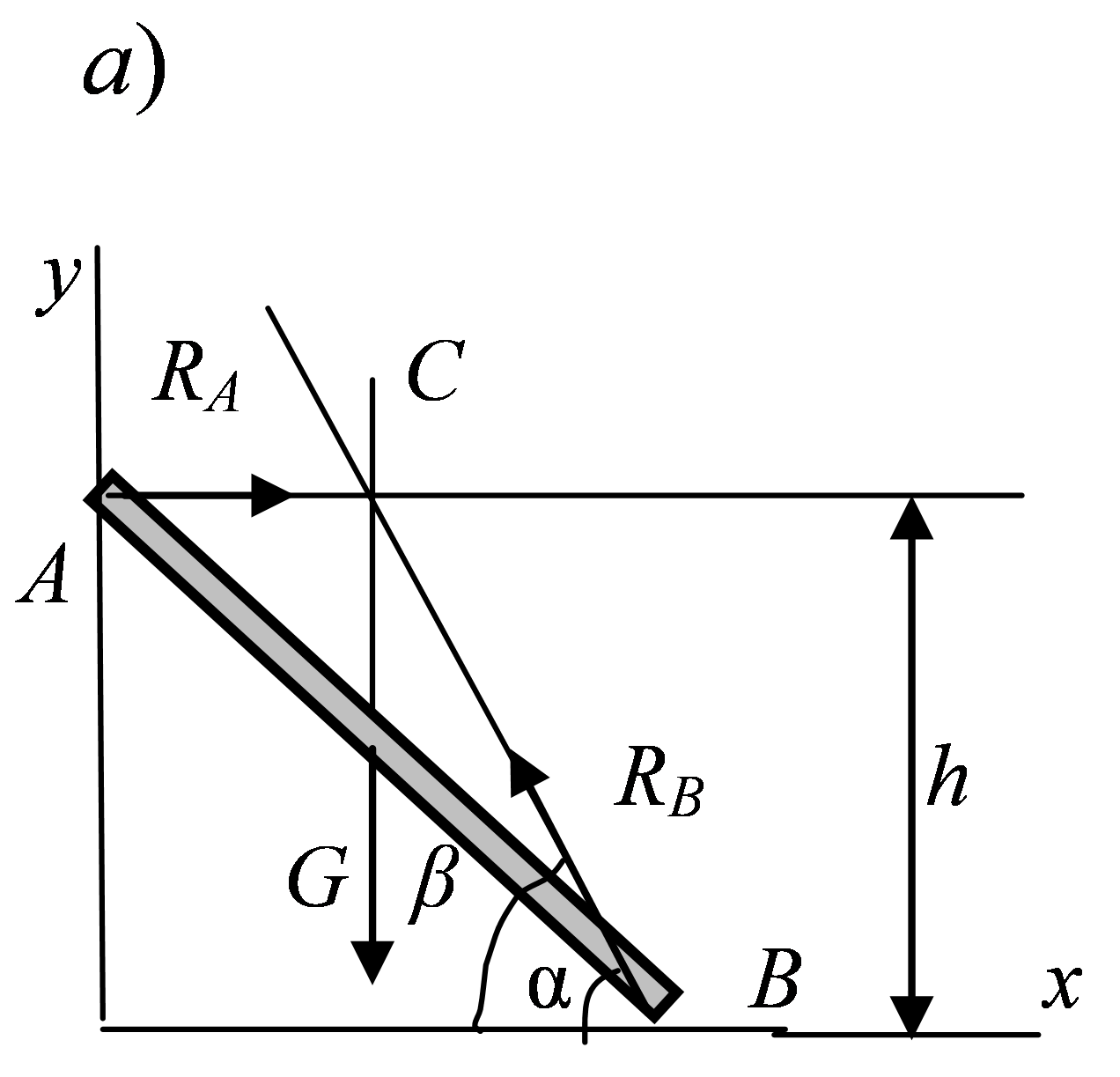
Рис. 1.2.14

При графическом решении (рис. 2.14, б) строим замкнутый треугольник векторов сил , , . Из него следует:

.

Задача 13. Груз весом G = 2 кН (рис. 1.2.15) удерживается краном, состоящим из двух невесомых стержней в шарнирах АВ и АС, прикрепленных к вертикальной стене и составляю­щих с ней углы α₁ = 60° и α₂ = 40°. В точке А подвешен блок, через который перекинут грузовой трос, идущий к блоку в точке D и составляющий со стеной угол α₃ = 60°.

Весом троса и блока, а также размерами блока можно пренебречь. Определить усилия в стержнях.

Решение. Рассмотрим находящийся в равновесии груз (рис. 1.2.16). На него действуют две силы: сила тяжести G и сила натяжения троса N₁. Поскольку система сил уравнове­шена, можно сделать очевидный вывод: сила натяжения троса направлена внутрь троса и по модулю равна весу груза N₁ = G.

Если для любого блока (рис. 1.2.17) пренебречь трением на его оси, то силы натяжения ветвей его троса одинаковы N₁ = N₂ (что легко видеть из уравнения моментов относи­тельно центра блока).

Рис. 1.2.15 Рис. 1.2.16 Рис. 1.2.17

Теперь в качестве объекта равновесия можно рассмот­реть мысленно вырезанный узел в точке А (или, что то же самое, блок с прилежащей к нему частью троса). На этот узел будут действовать силы натяжения ветвей троса N₁ и N₂ и реакции R₁ и R₂ стержней АВ и АС (рис. 1.2.18).

Рис. 1.2.18

Реакции опорных стержней направлены, как извест­но, вдоль этих стержней. Направим их внутрь стержней, считая изначально стержни растянутыми.

Составим теперь уравнения равновесия как уравне­ния проекций сил на оси (для системы сходящихся сил), учитывая, что силы R₁, R₂ и N₂ составляют углы α₁, α₂ и α₃ с осью у.

Отсюда, учитывая, что , получаем

Решая эту систему уравнений, находим R₁ = 0,611 кН, R₂ = –3,52 кН. Знак «минус» у величины реакции R₂ озна­чает, что она имеет направление, противоположное при­нятому, то есть стержень АС не растянут, а сжат.