- •Курс лекций по статике и кинематике
- •Раздел 1 Статика
- •Основные понятия и аксиомы статики
- •Аксиомы статики
- •5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.
- •2 Связи и их Реакции
- •3 СистемЫ сил
- •Лекция 2 система сходящихся сил
- •1 Проекции силы на ось и на плоскость
- •Равнодействующая сходящейся системы сил
- •3 Условия равновесия сходящейся системы сил Векторная форма
- •Аналитическая форма
- •Теорема о трех непараллельных силах
- •Лекция 3 теория пар сил
- •1 Момент силы относительно точки и оси
- •Момент силы относительно точки
- •Момент силы относительно оси
- •Аналитическое выражение моментов силы относительно координатных осей
- •2 Пара сил и ее свойства
- •3 Сложение пар сил и Условия равновесия пар сил
- •Условие равновесия
- •Условия равновесия пар
- •2 Приведение произвольной системы сил к заданному центру
- •3 Условия и уравнения равновесия произвольной системы сил Частные случаи приведения системы сил
- •Приведение системы сил к динаме (динамическому винту)
- •Теорема Вариньона о моменте равнодействующей
- •Уравнения равновесия произвольной пространственной системы сил
- •Равновесие пространственной системы параллельных сил
- •Равновесие произвольной плоской системы сил
- •Равновесие плоской системы параллельных сил
- •Лекция 5 фермы и составные конструкции
- •Классификация ферм
- •Способ вырезания узлов
- •3 Способ сечений (Риттера)
- •Определение реакций опор составных конструкций
- •Лекция 6 Трение
- •1 Трение покоя (сцепления)
- •Экспериментально установлено, что
- •2 Трение качения
- •3 Устойчивость при опрокидывании
- •Лекция 7 центр тяжести
- •1. Центр параллельных сил
- •2 Центр тяжести твердого тела
- •3 Методы определения центров тяжести
- •4 Центры тяжести простейших тел
- •5 Статические моменты и центр тяжести
- •6 Вспомогательные теоремы для определения положения центра тяжести
- •Раздел 2 Кинематика Лекция 8 кинематика точки
- •1 Предмет и задачи кинематики
- •2 Способы задания движения точки Векторный способ задания движения точки
- •Естественный способ задания движения точки
- •3 Скорость и ускорение точки при векторном спосоБе задания движения точки Определение скорости точки
- •Определение ускорения точки
- •4 Скорость и ускорение точки при координатном способе задания движения Определение скорости точки
- •Определение ускорения точки
- •2 Скорость и ускорение точки Скорость точки
- •Ускорение точки
- •4 Классификация движений точки
- •Равномерное и равнопеременное движение точки Равномерное движение точки
- •Равнопеременное движение точки
- •Лекция 10 простейшие движения твердого тела
- •1 Поступательное движение твердого тела
- •2 Вращательное движение твердого тела
- •3 Скорость и ускорение точек, вращающегося тела
- •4 Передаточные механизмы
- •Лекция 11 плоское движение твердого тела
- •Уравнения плоского движения твердого тела
- •2 Скорости точек тела при его плоском движении
- •3 Ускорение точек тела при его плоском движении
- •На этом основании
- •Лекция 12 мгновенный центр скоростей и ускорений
- •1 Мгновенный центр скоростей
- •2 Частные случаи определения мгновенного центра скоростей
- •3 Мгновенный центр ускорений
- •Угловая скорость вращения колеса
- •Действительно, имеем
- •2 Скорость точки при сложном движении
- •Таким образом
- •3 Ускорение точки при сложном движении
- •4 Ускорение кориолисово
- •Для тел, движущихся по поверхности Земли, ее вращение вокруг оси является переносным движением.
6 Вспомогательные теоремы для определения положения центра тяжести
При вычислении координат центров тяжести пользуются различными приемами, позволяющими упростить вычисления. Рассмотрим четыре вспомогательные теоремы, упрощающие в некоторых случаях нахождение центров тяжести.
Теорема 1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Теорема 2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.
На основе рассмотренных теорем можно определить положения центров тяжести некоторых симметричных линий, фигур и тел:
1) центр тяжести отрезка прямой лежит в его середине;
2) центры тяжести окружности, площади круга, поверхности и объема шара находятся в их геометрических центрах;
3) центры тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей;
4) центр тяжести периметра и площади правильного многоугольника находится в центре вписанного (или описанного) круга.
Теорема 3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести.
Пусть плоская фигура площадью F вращается вокруг оси у, лежащей в плоскости фигуры и не пересекающей ее. При вращении вокруг оси у контур этой фигуры описывает некоторую замкнутую поверхность, называемую поверхностью вращения. Тело, ограниченное этой поверхностью, называется телом вращения (рис. 7.9). Объем этого тела вращения определим как сумму бесконечно большого числа объемов элементарных круговых колец, образованных вращением вокруг оси у бесконечно малых площадок ΔFi. Радиус каждого кольца равен расстоянию этой площади от оси у, т. е. координате xi.
Объем элементарного кольца
![]() .
.
Объем тела вращения
![]() .
.
Здесь суммирование распространено на все площадки, входящие в состав данной площади F.
Сумму
![]() можно
определить из формулы:
можно
определить из формулы:
![]() .
.
Подставив это значение в выражение, определяющее объем тела вращения, получим
![]() .
(7.11)
.
(7.11)
где 2πхс - длина окружности, описанной центром тяжести фигуры.
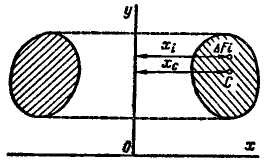
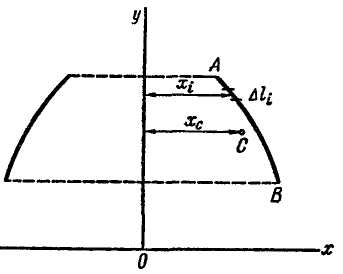
Рис. 7.9 Рис. 7.10
Теорема 4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центрам тяжести.
Пусть кривая АВ длиной L вращается вокруг оси у, лежащей в плоскости этой кривой, но не пересекающей ее. При вращения вокруг оси у эта кривая опишет некоторую поверхность вращения (рис. 7.10).
Разобьем кривую на бесчисленное множество бесконечно малых элементов длиной Δli. Поверхность, описанную каждым элементом, можно принять за поверхность усеченного конуса.
Как известно из геометрии, площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на длину образующей. Поэтому площадь поверхности, образованной вращением элемента кривой Δli , можно определить по формуле
![]() ,
,
где хi - радиус окружности, равный расстоянию середины элемента от оси у.
Площадь поверхности вращения
![]() ,
,
здесь
суммирование распространено на все
элементы Δli
кривой АВ.
Сумму
![]() определим из формулы:
определим из формулы:
![]() .
.
Подставив это значение в выражение, определяющее площадь поверхности вращения, получим
![]() .
.
Таблица 7.1
Центры тяжести некоторых фигур
Центр тяжести |
Рисунок |
Формула |
Центр тяжести площади треугольника |
|
|
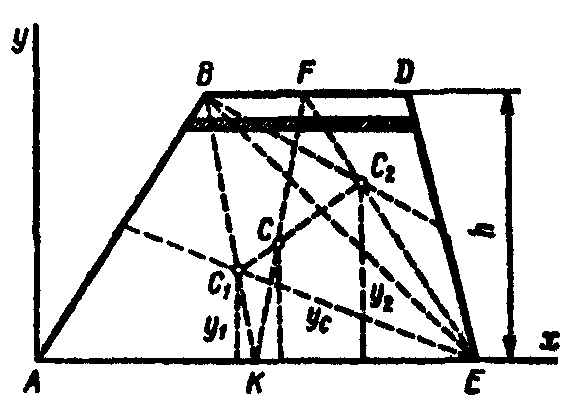
Центр тяжести площади трапеции |
|
|
Центр тяжести дуги окружности |
|
|
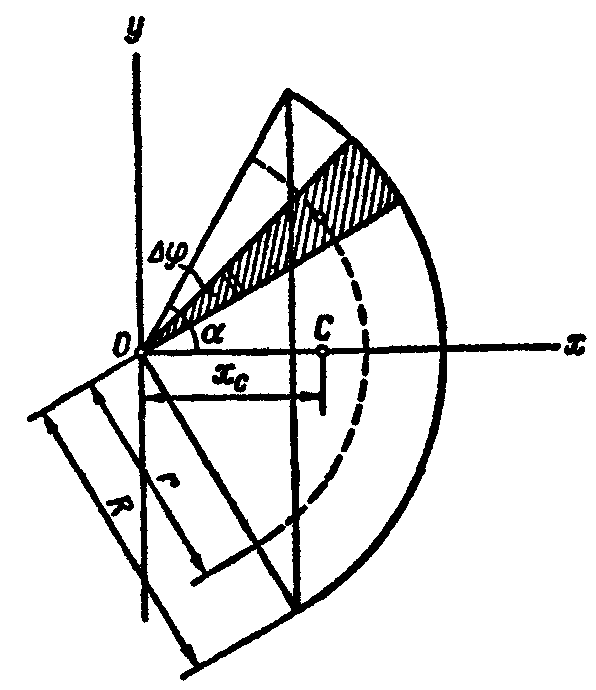
Центр тяжести площади сектора круга |
|
|
Центр тяжести объема пирамиды |
|
|
Центр тяжести объема конуса |
|
|