Равновесие плоской системы параллельных сил

Для плоской системы параллельных сил можно составить два уравнения равновесия. Если силы параллельны оси у, то можно составить две формы уравне­ний равновесия.

Первая форма уравнений равновесия

1. .

2. .

Второе уравнение можно составить относительно любой точки.

Вторая форма уравнений равновесия

1. .

2. .

Задача 11. Определить реакции опор, если Р= 6 кН, q = 1 кН/м, М= 4 кНм (рис. 4.8).

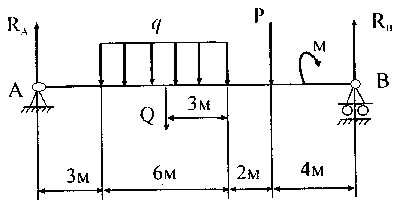
Рис. 4.8

Решение. Рассмотрим равновесие балки АВ под действием силы , момента , равномерно распределенной нагрузки интенсивности q и реакций связей . Составим два уравне­ния равновесия по первой форме. Равномерно распределенную нагрузку заменим равнодействующей кН, которая приложена к середине нагруженного участка:

1. .

2. .

Находим из (2)

,

из (1)

.

Ответ. .

Задача 12. На двухконсольную балку (рис. 2.2.1, а) с шарнирно-неподвижной опорой в точке А и шарнирно-подвижной в точке В действуют сосредоточенная сила F = 10 кH, пара сил с М = 40 кH/м и равномерно распределенная нагрузка интенсивностью q = 0,8 кН/м. Определить реакции опор.

Решение. Составление расчетной схемы (рис. 2.2.1, б). Объект равновесия - балка СD. Активные силы F и , которая приложена в точке О посередине участка АD, образуют плоскую параллельную систему сил.

После освобождения балки от связей и замены их реакциями R_A, R_B получаем уравновешенную систему, состоящую из четырех параллельных сил и одной пары сил (момента). Ось х направляем вдоль оси балки, ось у - вертикально вверх из точки С.

2. Условия равновесия:

.

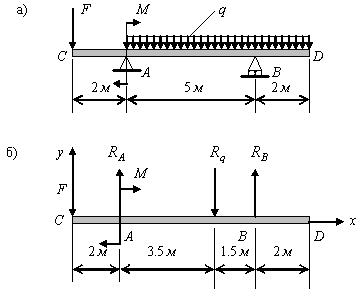
Рис. 2.2.1

3 . Составление уравнений равновесия

;

.

4. Определение искомых величин, проверка правильности решения и анализ полученных результатов. Уравнения равновесия содержат две неизвестных величины, задача статически определима, но каждое из уравнений содержит обе реакции. Поэтому из первого уравнения, как более простого, выразим R_A через неизвестную R_B и подставим ее значение во второе уравнение:

;

;

; ;

.

Для проверки правильности решения составим любое уравнение равновесия, не использованное ранее для определения неизвестных, например, запишем уравнение моментов относительно точки А:

т.е. уравнение удовлетворяется тождественно, что подтверждает правильность решения – реакции определены верно и их направления соответствуют показанным на расчетной схеме.

Лекция 5 фермы и составные конструкции

1. Классификация ферм

Фермой называется конструкция, составленная из стержней, концы которых соединены между собой шарнирами так, что стержни не могут иметь относительных перемещений, т.е. вся конструкция представляет собой неизменяемую систему. Другими словами, фермой называется геометрически неизменяемая шарнирно-стержневая конструкция (рис. 5.1). Места соединения стержней называются узлами ферм, а те узлы, которыми ферма опирается на основание, называются опорными узлами (рис. 5.2, 5.3, 5.4).

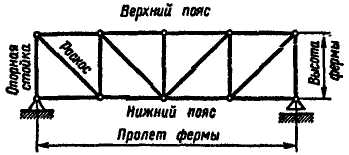
Рис. 5.1 Рис. 5.2

Рис. 5.3 Рис. 5.4

Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру - нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные - раскосами.

Фермы часто употребляются в различных сооружениях, например, при стройке мостов, стропил, грузоподъемных машин. При этих условиях допускают простой, элементарный расчет, не говоря уже о значительной экономии материалов. Расчет фермы становится более простым, если под действием внешних сил стержни фермы подвергаются только продольным усилиям, т.е. растяжению или сжатию. Для этого должны иметь место следующие условия:

стержни ферм должны быть прямолинейны и соединены своими концами шарнирами без трения;

силы должны быть приложены в узлах ферм.

На практике эти условия, как идеальные, осуществляются не вполне, а с возможным приближением.

Если оси стержней фермы лежат в одной плоскости, то ферма называется плоской, в противном случае - пространственной.

Рассмотрим плоские фермы.

Найдем наименьшее число стержней, необходимых для построения фермы, образованной из треугольников и имеющий n узлов (рис. 5.1, а).

Чтобы связать первые три узла, необходимо три стержня; для жесткого присоединения каждого из остальных (n-3) узлов нужно по два стержня. Следовательно, для того чтобы ферма обладала жесткостью (т.е. чтобы стержни не могли иметь относительных перемещений), необходимо, чтобы число стержней было:

.  (5.1)

Если число стержней

,

то конструкция не будет обладать жесткостью, т.е. она не будет фермой. Если же

,

то ферма будет иметь «лишние» стержни.

Равенство (5.1) называется условием жесткости. Если ферма обладает жесткостью, то ее можно рассматривать как абсолютно твердое тело, находящееся под действием активных сил и реакций связей. Будем предполагать, что эти силы приложены в узлах ферм и, если ферма плоская, действуют в плоскости ферм.

При равновесии такая система сил должна удовлетворять трем уравнениям равновесия. На каждый узел фермы будет действовать плоская система сходящихся сил, состоящая из внешних сил, действующих на ферму, и внутренних - усилий в самих стержнях, которые будут, согласно сделанным допущениям, иметь направления стержней. Поэтому система сил, действующих на каждый узел, должна удовлетворять двум уравнениям равновесия.

Таким образом, все действующие на ферму внешние силы (активные и реакции) и усилия в стержнях фермах должны удовлетворять 2n уравнениям, где n - число узлов. В число этих 2n уравнений будут входить три уравнения, выражающие условия равновесия внешних сил, поэтому для определения усилий в стержнях фермы остаются (2n-3) уравнений.

Если число стержней фермы N=2n-3, то эти усилия могут быть определены из уравнений статики и, следовательно, ферма будет статически определимой.

Если же N>(2n-3), то усилия в стержнях посредством одних только уравнений статики абсолютно твердого тела определить нельзя и ферма будет статически неопределимой.

Следовательно, условие жесткости (5.1) является и условием статической определенности.