Естественный способ задания движения точки

Рассмотрим естественный способ задания движения точки, применяемый в случае, когда траектория точ­ки заранее известна. Траекторией может быть как прямая, так и кривая линия (рис. 8.5).

Рис. 8.5

Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Положение движущейся точки М на траектории будем определять дуговой координатой, т. е. расстоянием ОМ = s, отложенным по траектории от начала отсчета О.

Расстояния, отложенные в одну сторону от точки О, будем считать положительными, а в противоположную - отрицательными, т. е. уста­новим направление отсчета дуговой координаты.

При движении точки М расстояние s от этой точки до неподвиж­ной точки О изменяется с течением времени, т. е. дуговая координата s является функцией времени:

. (8.5)

Эта зависимость называется уравнением движения точки.

Если вид функции f(t) известен, то для каждого значения t можно найти значение s, отложить соответствующее расстояние по траектории и указать, где находится движущаяся точка М в этот момент времени.

Таким образом, движение точки определено, если известны следую­щие элементы: траектория точки, начало и направление отсчета дуговой координаты и уравнение движения s =f(t).

Дуговую координату точки не следует смешивать с длиной пути σ, пройденного движущейся точкой. Дуговая координата s точки М в некоторый момент времени t может быть равна пути σ, пройденному точкой за промежуток времени [0, t], только в том случае, если движе­ние точки начинается из точки О и совершается в положительном на­правлении.

.

3 Скорость и ускорение точки при векторном спосоБе задания движения точки Определение скорости точки

Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.

При векторном способе задания движения положение движущейся точки в каждый момент времени определяется радиусом-вектором , который является функцией времени . Пусть в момент времени t точка занимает положение М, определяемое радиусом-вектором , а в момент - положение M₁, определяемое радиусом-век­тором (рис. 8.6). Из треугольника ОММ₁,

.

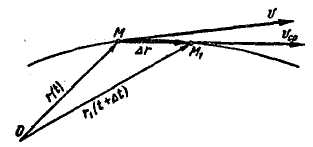
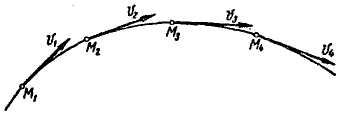
Рис. 8.6 Рис. 8.7

При перемещении точки ее радиуc-вектор получает приращение:

.

Из двух последних равенств следует, что вектор перемещения точки является приращением радиуса-вектора точки за промежу­ток времени t.

Отношение вектора перемещения к промежутку времени t, в течение которого произошло это перемещение, представляет собой вектор средней скорости воображаемого движения точки по хорде ММ₁:

.

Направление вектора совпадает с направлением Δ . При умень­шении промежутка времени Δt и приближении его к нулю вектор Δ также стремится к нулю, а вектор - к некоторому пределу. Этот предел является вектором скорости точки в момент t:

.

Так как Δt - приращение скалярного аргумента t, а Δ - прираще­ние вектора-функции , то предел отношения при явля­ется векторной производной от по t:

Отсюда

Таким образом, вектор скорости точки в данный момент равен производной от радиуса-вектора точки по времени.

Вектор направлен по хорде MM₁ в сторону движения точки. Когда Δt стремится к нулю, точка M₁ стремится к точке М, т. е. предельным положением секущей MM₁ является касательная.

Из этого следует, что вектор скорости точки направлен по касательной к траектории в сторону движения точки.

При движении точки по криволинейной траектории направление вектора скорости непрерывно изменяется (рис. 8.8).

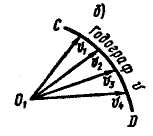
Рис. 8.8

Скорость точки при неравномерном криволинейном движении изменяется как по модулю, так и по направлению.

Отметим ряд положений движущейся точки на траектории M₁, M₂, M₃, М₄ и покажем в этих положениях скорости точки (рис. 8.8,а).

Выбрав в пространстве некоторую неподвижную точку О₁, отло­жим от этой точки векторы, геометрически равные скоростям (рис. 8.8,б). Если от точки О₁ отложить скорости, соответствующие всем поло­жениям точки М на кривой АВ, и соединить концы этих векторов, то получится линия CD, являющаяся годографом скорости.

Таким образом, годограф скорости представляет собой геометри­ческое место концов векторов скорости движущейся точки, отложен­ных от одной и той же произвольной точки пространства.

Изобразим на рис. 8.9, а траекторию точки АВ и ее скорость в произвольный момент времени t, а на рис. 8.9, б - годограф ско­рости CD этой точки.

Проведем через точку О₁ оси координат X, Y, Z, параллельные основным осям х,y,z. Тогда радиусом-вектором любой точки N годографа скорости CD будет скорость , а координаты точек годографа X, У, Z будут равны проекциям скорости на оси координат:

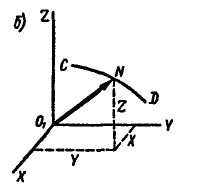
Рис. 8.9

.

Эти уравнения являются параметрическими уравнениями годографа скорости.