Действительно, имеем

а потому найдем

При АВ≠0

Пример 1. Колесо радиуса r = 1 м катится без скольжения уско­ренно по прямолинейному рельсу, имея в данный момент времени скорость центра v_o = 1 м/с и ускорение центра a_о — 1 м/с² (рис. 4.1.1). Определить угловую скорость и уг­ловое ускорение колеса, скорости и ускорения точек его обода М₁, М₂, М₃ и М₄, а также установить положение МЦС и МЦУ колеса.

Рис. 4.1.1 Рис. 4.1.2

Решение.

I. Определение скоростей. У колеса, катящегося без скольжения по неподвижной поверхности, МЦС (точка Р) находится в точке касания с этой поверхностью (рис. 4.1.2). В данном случае это точка M₁ (М₁ = Р): .

Скорости точек плоской фигуры пропорциональны рас­стояниям от этих точек до МЦС: , где ω — уг­ловая скорость тела. Применяем эту формулу к точке О: v_o =ω|ОР| = ωr, откуда ω = v_o/r = 1 с^–1.

Для точек М₂ и М₃ расстояния до точки Р одинаковы, поэтому одинаковы и модули скоростей этих точек:

м/с.

Скорость точки М₃ м/с. Направления скоростей перпендикулярны отрезкам, со­единяющим точки с МЦС.

Для вычисления скоростей можно было использовать также и теорему о сложении скоростей, выбрав в качестве полюса центр колеса: , где v_MO = ω|МО|. Ско­рость перпендикулярна отрезку МО и направлена по ходу вращения.

Можно было также пользоваться и следствием из этой теоремы о равенстве проекций скоростей точек на ось, проходящую через эти точки.

2. Определение ускорений. Вычислим сначала угловое ускорение колеса, формально дифференцируя выражение угловой скорости

.

В данном случае использован тот факт, что движение центра колеса прямолинейное и, следовательно, касатель­ное ускорение точки совпадает с полным ускоре­нием.

Для вычисления ускорений точек колеса применим теорему о сложении ускорений: , выбрав в качестве полюса центр колеса. Вращательное ускорение точки относительно полюса и направлено перпендикулярно отрезку МО по ходу угло­вого ускорения а центростремительное все­гда направлено от точки к полюсу.

Тогда для точек М₁, М₂, М₃ и М₄ получим , . Направления их показаны на рис. 4.1.3.

Рис. 4.1.3 Рис. 4.1.4

Складывая в каждой точке три вектора, модули кото­рых равны по 1 м/с², получаем м/с², м/с².

3. Определение положения МЦУ. Найти положение МЦУ (точки Q, ускорение которой равно нулю) можно на основании известных положений:

а) все ускорения составляют один и тот же угол β с направлениями из этих точек на МЦУ:

.

В данном случае tg β = 1 и β = 45°. Повернув каждое ускорение на угол β по ходу углового ускорения, мы на пересечении лучей и получим точку Q (рис. 4.1.4). Итак, МЦУ колеса при принятых исходных данных оказывает­ся на середине отрезка М₁M₄;

б) ускорения точек пропорциональны расстояниям от этих точек до МЦУ:

.

В силу одинаковости расстояний до МЦУ в данном слу­чае оказываются равны между собой модули ускорений , а также . Из всех точек колеса самое большое ускорение будет иметь точка D (рис. 4.1.4):

.

Ответ:

ω = 1 с^–1; ε = 1 с^–2; = 0; м/с; = 2 м/с; ; .

Пример 2. Кривошип OA длиной 0,2 м вращается рав­номерно с угловой скоростью ω_OA = 10 с^–1 и при­водит в движение шатун АВ длиной 1 м. Пол­зун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с вертикалью угол 45° (рис. 4.1.5).

Решение.

1. Определение скоростей. Вычис­лим скорость точки А как точки вра­щающегося кривошипа:

.

Она направлена перпендикулярно ОА (рис. 4.1.6).

Рис. 4.1.5

Скорость v_B ползуна направлена по направляющей вертикально.

Для шатуна АВ, совершающего плоское движение, теперь известны направления скоростей двух его то­чек: А и В. Восставляя перпендику­ляры к векторам этих скоростей, на­ходим точку Р их пересечения — МЦС шатуна.

Используя известную формулу для скоростей точек при плоском движении, получаем ; .

Рис. 4.1.6 Рис. 4.1.7

Из треугольника АВР имеем |АР| = 1 м; |ВР| = м, и тогда

.

2. Определение ускорений. Вычислим сначала ускоре­ние точки А как точки кривошипа: .

Здесь вращательное ускорение , так как , поскольку .

Тогда полное ускорение точки А равно центростремительному

и направлено к оси вращения — точке О (рис. 4.1.5).

Для вычисления ускорения точки В воспользуемся тео­ремой о сложении ускорений, взяв точку А в качестве полюса:

. (*)

Центростремительное ускорение точки В в относи­тельном вращении вокруг точки А по модулю равно , и направлено от точки В к полю­су — точке А.

Модуль вращательного ускорения определяется по формуле и пока не может быть вычислен, поскольку неизвестна величина углового ускорения . Направление вектора также не может быть определе­но однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедлен­ным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление совпадет с направле­нием , а вектор направим перпендикулярно от­резку ВА по ходу углового ускорения.

Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать дви­жение ползуна ускоренным и направим ускорение в ту же сторону, что и скорость (рис. 4.1.6, 4.1.7).

Теперь в равенстве (*) все ускорения имеют определен­ное направление, и мы можем записать это уравнение в проекциях на выбранные оси:

.

Из последнего уравнения получаем , тогда из первого уравнения

.

Отсюда следует, что

.

Отрицательные знаки у величин и показывают, что их истинные направления противоположны принятым.

Ответ: = 2 с^–1; = –16 с^–2; v_B = 2 м/с; а_В = = 4 м/с².

Пример 3. Круглый цилиндр А обмотан тонким тросом, конец которого В закреплен неподвижно. Цилиндр падает без начальной скорости, разматывая трос. Значение скорости оси цилиндра определяется формулой , где g – ускорение силы тяжести; у – расстояние, пройденное центром цилиндра, отсчитываемое от начального положения, т.е. координата точки А. Точка А движется прямолинейно по вертикали. Радиус цилиндра равен r. Определить скорости четырех точек на ободе цилиндра, расположенных на концах взаимно перпендикулярных диаметров, изображенных на рис. 4.1.8.

Решение. Мгновенный центр скоростей цилиндра находится в точке D, где неподвижная часть троса BD соприкасается с цилиндром. В этом месте скорости точек троса и цилиндра, находящихся в соприкосновении, равны между собой и, следовательно, равны нулю. Скорости остальных точек пропорциональны расстояниям до мгновенного центра скоростей и перпендикулярны к мгновенным радиусам. Величина скорости точки Е определяется из пропорции

,

откуда, учитывая формулу (1), находим, что

. (2)

Рис. 4.1.8

Направление скорости точки Е перпендикулярно к мгновенному радиусу DE, т. е. параллельно скорости точки А. Скорости точек С и Н равны по величине, так как они отстоят от мгновенного центра скоростей, точки D, на одинаковых расстояниях DC=DH=r . Величины этих скоростей определяются из пропорции

,

откуда

, (3)

направлены эти скорости перпендикулярно к мгновенным радиусам CD и HD (рис. 4.1.8, б).

Формулы (2) и (3) определяют величину скоростей точек С,Е,Н как функцию пройденного центром цилиндра расстояния у. Найдем величину этих скоростей как функцию времени.

Так как точка А движется прямолинейно по вертикали, то

.

Отделяя переменные, имеем

Интегрируя это дифференциальное уравнение и полагая у=0 при t=0, находим уравнение движения центра цилиндра

.

Подставляя это значение расстояния у в формулы (2) и (3), получаем

Величину скорости точек С и Н можно также найти на основании теоремы о равенстве проекций скоростей двух точек плоской фигуры на прямую, соединяющую эти точки. Скорости точек С и Н составляют углы 45^о с линией САН, а скорости точки А направлена по этой прямой. Следовательно,

откуда

Пример 4. Прямоугольник ABCD совершает плоское движение. Ускорение точки А в данный момент равно =2 см/с² и составляет угол 30^о с прямой АВ. Ускорение точки В равно =6 см/с² и образует угол 60^о с прямой ВА. Длина сторон: АВ=10 см, ВС=5 см. Определить мгновенную угловую скорость и мгновенное угловое ускорение прямоугольника, а также ускорение точки С.

Решение. Выбираем точку А за полюс. Тогда ускорение точки В

. (1)

Проектируем векторное равенство (1) на оси х и у. В проекции на ось х имеем

откуда

Рис. 4.1.9

Теперь найдем величину мгновенной угловой скорости фигуры

Проецируя векторное равенство (1) на ось у, получаем

.

Отсюда определяется вращательное ускорение точки В:

Далее находим величину мгновенного углового ускорения фигуры

.

Угловое ускорение фигуры направлено по оси z в отрицательную сторону.

Переходим к определению ускорения точки С. Согласно формуле распределения ускорений, выбирая точку В за полюс, имеем (рис. 4.1.9, б):

.

Проецируя это равенство на оси х и у, находим

Теперь легко найдется величина ускорения точки С:

.

Направление а_С определится формулами

Пример 1. Кривошип ОА нецентрального кривошипно-шатунного механизма (рис. 8.2) вращается с угловой скоростью ω₁. Опре­делить скорости точек В и М, а также угловую скорость шатуна АВ для заданного положения звеньев механизма, если известно: φ =30°; ω₁ = 2 рад/с; ОА = 0,4 м; АВ = 0,8 м; АМ=0,4 м; h = 0,2 м.

Рис. 8.2

Решение. Далее будут рассмотрены три способа решения задачи.

Первый способ - разложение движения звена на переносное по­ступательное и относительное вращательное.

Разложим движение второго звена на переносное поступатель­ное и относительное вращательное. За полюс принимаем точку А и запишем теорему сложения скоростей для точки В.

.

.

Строим кинематическую схему механизма в выбранном масшта­бе (1:20), указываем на схеме направление скоростей точек A и В.

Скорость точки В направлена горизонтально, так как точка В принадлежит и шатуну и ползуну, а движение ползуна поступатель­ное прямолинейное по горизонтали. Таким образом, траектория точ­ки В - горизонтальная прямая, вдоль которой и направлена скорость точки В. Точка А шатуна совпадает с точкой А кривошипа ОА и движется по окружности радиуса ОА, так как движение кривошипа вращательное вокруг центра О.

Зная угловую скорость кривошипа, найдем величину скоро­сти точки А

м/с.

Скорость направлена перпендикулярно прямой АВ, а пря­мая АВ образует с направлением скорости точки В угол 30° (так подобраны размеры звеньев), следовательно, скорость образует с горизонталью угол 60°, а скорость точки А перпендикулярна ОА (касательная перпендикулярна к радиусу) и образует с горизонта­лью также угол 60°.

Для определения скорости и скорости точки В построим в масштабе (1:40) треугольник скоростей (рис. 8.2 вверху справа).

На основании вышеизложенного этот треугольник равносторон­ний, следовательно,

.

Угловую скорость шатуна относительно полюса А находим по формуле

рад/с.

Заметим, что угловая скорость шатуна вокруг полюса равна аб­солютной угловой скорости.

Далее, зная угловую скорость шатуна, найдем скорость точки М в соответствии с теоремой сложения скоростей для этой точки

. (8.2)

Относительную скорость можно найти по формуле

,

или графически, основываясь на том, что относительные скорости точек пропорциональны их расстояниям до полюса. Метод построе­ния ясен из рис. 8.2.

Из треугольника скоростей (см. рис. 8.2 внизу справа) с помо­щью измерений по масштабу находим

м/с.

Рис. 8.3

Задачу можно решить и без по­строения треугольника скоростей, на­пример, методом проекций. Найдем скорость точки В шатуна следующим образом: в точке В построим систему координат Вху (рис. 8.3), которая имеет­ся и на рис. 8.2. Изобразим векторы скоростей и и отметим величины углов (рис. 8.3). Далее, спроектируем векторное уравнение

на ось Вх.

.

Отсюда следует, что скорость точки В по величине равна скорости точки А. Если спроектировать указанное уравнение на вертикальную ось, то сразу определяется относительная скорость и, следова­тельно, угловая скорость шатуна. Эта операция предоставляется студенту для самостоятельного решения.

Тот же результат получится, если использовать теорему о про­екциях скоростей. Так как векторы скоростей точек А и В образуют один и тот же угол с прямой А В, то эти скорости равны по величине.

Ответ: ω₂ = 1 рад/с; v_B = 0,8 м/с; v_M = 1,06 м/с.

Второй способ - опреде­ление скоростей точек и уг­ловой скорости звена с по­мощью мгновенного центра скоростей.

На рис. 8.4 изобразим в масштабе длин кинематиче­скую схему механизма и укажем мгновенный центр скоростей шатуна.

По построению треуголь­ник АР₂В равносторонний, следовательно, скорость точ­ки В равна скорости точки А. Угловая скорость шатуна

рад/с.

Скорость точки М равна

.

Рис. 8.4

Расстояние Р₂М можно определить измерением или найти по из­вестной теореме косинусов

.

И тот, и другой метод дают одинаковый результат: Р₂М= 0,4 м. В соответствии с этим v_M = 0,4 м/с.

Ответ: ω₂ = 1 рад/с; v_B = 0,8 м/с; v_M = 1,06 м/с.

Третий способ - разложение движения звена на два вращения.

Движение шатуна разлагаем на два вращательных движения -переносное вращение вместе с кривошипом вокруг центра О и отно­сительное вращение вокруг центра А. Итак, точка О - центр пере­носного вращения, точка А - центр относительного вращения и точ­ка Р - центр абсолютного вращения.

Рис. 8.5

Заметим, что центры переносного, относительного и абсолют­ного вращений лежат на одной прямой и это есть общее правило. При этом угловые скорости переносного, относительного и пере­носного вращений связаны соотношением

.

При решении данной задачи перепишем эту формулу в таких обозначениях:

.

Заметим, что из всех угловых скоростей известна только угловая скорость кривошипа Ш\, которая для шатуна является переносной угловой скоростью.

Запишем теорему сложения скоростей для точки В

.

Переносная скорость точки В перпендикулярна прямой ОВ и ее величина определяется по формуле

.

Расстояние ОВ измеряем, или находим геометрически, исполь­зуя метрические соотношения в треугольнике ОАВ. В результате получаем ОВ = 1,06 м. Тогда переносная скорость равна 2,12 м/с. Относительная скорость направлена перпендикулярно АВ, а абсо­лютная скорость точки В направлена горизонтально. Этих данных достаточно для построения треугольника скоростей, который по­строен на рис. 8.5 вверху справа. Измеряя построенные векторы в выбранном масштабе, получаем

м/с; м/с.

Зная относительную скорость точки В, определяем угловую ско­рость шатуна в относительном вращении относительно кривошипа

рад/с.

По этой формуле определяется только абсолютная величина от­носительной угловой скорости. Изобразив вектор относительной скорости на кинематической схеме механизма (рис. 8.5), видим, что шатун вращается вокруг центра А по часовой стрелке. Это озна­чает, что относительная угловая скорость отрицательна.

Переходим к определению скорости точки М. Теорема сложения скоростей

.

Переносная скорость точки М направлена перпендикулярно прямой ОМ, относительная скорость направлена перпендикулярно прямой MB, а величины этих скоростей определяются по формулам

.

После вычислений находим м/с; м/с.

Строим треугольник скоростей (рис. 8.5 внизу справа), из кото­рого находим v_M = 1,06 м/с.

Ответ: ω₂ = 1 рад/с; v_B = 0,8 м/с; v_M = 1,06 м/с.

Пример 2. Механизм, изображенный на рис. 8.6, называется шарнирным четырехзвенником с присоединенной диадой. Звенья ме­ханизма имеют следующие размеры: О₁А = 0,3 м; АВ = 0,25 м; O₂D = 0,3 м; DB = 0,2 м; О₂Е=0,3 м; O₁O₂=0,6 м; DM=0,9 м; звено О₁А перпендикулярно О₁О₂. Кривошип О₁А вращается с угловой скоро­стью ω₁=4 рад/с по часовой стрелке. Необходимо определить угло­вые скорости всех звеньев механизма и скорости точек B,D, Е и М.

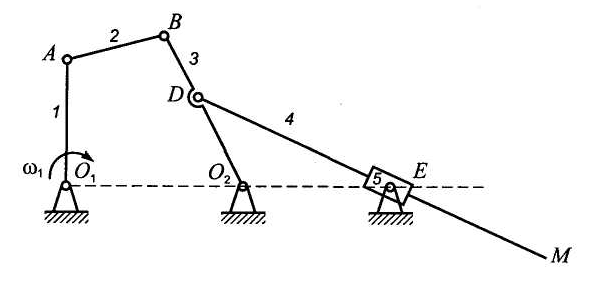
Рис. 8.6

Решение. Механизм работает следующим образом. При враще­нии кривошипа О_ХА звено АВ совершает сложное плоскопараллель­ное движение, а второй кривошип О₂В вращательное движение, но при этом он не делает полного оборота, а совершает колебания от­носительно некоторого среднего положения. Звено DM при этом скользит поступательно вдоль цилиндра Е и одновременно с этим вращается вместе с цилиндром относительно оси его вращения.

Задачу будем решать в следующем порядке. Сначала найдем уг­ловые скорости всех звеньев и скорости заданных точек с помощью мгновенных центров скоростей. Затем найдем угловые скорости второго и третьего звена с помощью разложения движения второго звена на переносное поступательное и относительное вращательное. Далее, найдем угловые скорости четвертого и пятого звена и ско­рость точки М с помощью разложения движения четвертого звена на переносное вращательное и относительное поступательное. Затем найдем скорость точки М с использованием теоремы о скоростях и теоремы о проекциях скоростей.

Для выполнения намеченного плана изобразим в масштабе (1:10) кинематическую схему механизма, на которой построим МЦС звеньев и направления скоростей точек.

Мгновенные центры скоростей находим так. Совершенно оче­видно, что точка А движется по окружности радиуса О₁А, а точка В по окружности радиуса О₂В. Скорости точек А и В направлены по касательным к соответствующим окружностям. Следовательно, МЦС второго звена лежит на пересечении прямых О₁А и О₂В, т.е. в точке Р₂. Сложнее определить МЦС четвертого звена. Здесь сразу опреде­ляется только направление скорости точки D, так как ее траектория есть окружность с центром в точке О₂. На четвертом звене нет ника­кой другой точки, кроме точки D, для которой была бы известна траектория. Поэтому поступаем следующим образом. Разлагаем движение четвертого звена на переносное вращательное вместе с ци­линдром Е и относительное поступательное относительно цилиндра.

Далее, запишем теорему сложения скоростей для точки Е чет­вертого звена.

.

Заметим, что, согласно определению, переносная скорость точки Е четвертого звена равна абсолютной скорости точки Е пятого звена. Но эта скорость равна нулю, так как является для цилиндра Е центром вра­щения. Таким образом, абсолютная скорость точки Е четвертого звена равна относительной скорости, направление которой известно, так как в относительном движении четвертое звено движет­ся вдоль цилиндра прямолинейно. Дальнейшие построения понятны из рис. 8.7.

Рис. 8.7

Далее, необходимо составить алгоритм для определения угло­вых скоростей звеньев и скоростей точек. Для этого предварительно найдем расстояния АР₂, ВР₂, P₄D, P₄E и Р₄М.

Измерения дают результаты:

АР₂ = 0,27 м; ВР₂ = 0,34 м; P₄D = 0,6 м; P₄E =0,24 м, Р₄М =0,4 м.

Дальнейшие вычисления производим по формулам

После вычислений получаем ответ.

Ответ: v_B = 1,5 м/с; ω₂ = 4,4 м/с; ω₃ = 3 рад/с; ω₄ = 1,5 рад/с;

v_E = 0,35 м/с; v_D = 0,9 м/с; v_M = 0,6 м/с; ω₅ = ω₄.

Определение угловых скоростей второго и третьего звена с по­мощью разложения движения.

Для решения задачи изобразим на рис. 8.8 фрагмент кинемати­ческой схемы заданного механизма.

Рис. 8.8

Разложим движение второго звена на переносное поступатель­ное и относительное вращательное. За полюс принимаем точку А и записываем теорему сложения скоростей для точки В.

.

Скорость точки А счи­таем известной и равной 1,2 м/с. Скорость точки В известна по направлению. Она перпендикулярна О₂В. Скорость точки В относи­тельно полюса А перпенди­кулярна АВ.

Этих данных достаточ­но для построения тре­угольника скоростей, кото­рый построен на рис. 8.8.

С помощью измерений находим

=1,1 м/с; =1,5 м/с.

Далее, вычисляем угловые скорости

рад/с; рад/с.

Определение угловой скорости четвертого звена и скорости точки М методом разложения движения.

Разложим движение четвертого звена на переносное вращатель­ное и относительное поступательное. Точка Е - центр переносного вращения. Будем считать известной скорость точки D, которая равна 0,9 м/с.

Запишем для точки D теорему сложения скоростей

.

Относительная скорость точки Е направлена параллельно пря­мой DE, переносная - перпендикулярно этой прямой.

Таким образом, зная абсолютную скорость точки и направления всех скоростей, находим переносную и относительную скорости. Для этого достаточно построить параллелограмм скоростей (рис. 8.9).

Найдем скорость точки М. По той же теореме сложения скоро­стей, что и для точки D, имеем

.

Рис. 8.9

Так как относительное движение четвертого звена относительно цилиндра поступательное, то относительные скорости всех точек равны и

м/с,

а переносная скорость точки М находится геометрически. Для этого через конец вектора переносной скорости точки D и точку Е прово­дим прямую до пересечения с перпендикуляром к ME. Таким обра­зом, переносная и относительная скорости, найденные из параллело­грамма скоростей равны соответственно 0,49 м/с и 0,35 м/с.

Угловые скорости четвертого и пятого звена находим по формуле

рад/с.

Таким образом, определяется положение конца вектора перенос­ной скорости. Сложив геометрически переносную и относительную скорости точки М, получим абсолютную скорость, равную 0,6 м/с.

Ответ: ω₄ = ω₅ = 1,5 рад/с; v_M = 0,6 м/с.

Пример 3. Решим такую задачу. Пусть скорость точки D изо­бражается вектором . Необходимо построить в том же масштабе скорость точки М без вычислений.

Решение. Изобразим фрагмент заданного механизма и скорость точки D.

Рис. 8.10

Спроектируем скорость точки D на прямую DM. Величина скорости точки Е равна этой проекции. Исходя из этого, строим ско­рость точки Е. Проекция скорости точки М на прямую DM равна отрезку MG = DF по теореме о проекциях скоростей. Следовательно, конец вектора скорости точки М лежит на перпендикуляре к прямой DM из точки G. С другой стороны, концы векторов скоростей точек D, Е и М лежат на одной прямой. Проводим прямую через концы векторов скоростей точек D и Е и в точке пересечения этой прямой с прямой GK находим точку К, в которой находится конец вектора скорости точки М.

Пример 4. Определить для заданного положения механизма (рис. 8.11) угловые скорости всех звеньев и скорости точек А, В, С, D, E, F, М. Размеры звеньев механизма: ОА =0,2; АВ = 0,3; ВК=СК= = 0,4; СЕ=0,4; ОК=0,6; ED=0,2; l = 0,4; EM=MF=0,25 м. Кривошип ОА вращается с угловой скоростью ω₁ = 2 рад/с.

Рис. 8.11

Решение. Определим положение мгновенных центров скоро­стей всех звеньев, направления движений каждого звена и направления скоростей точек. Все это показано на рис. 8.12. При выполнении этого построения обратим внимание на следующее. Так как прямая КС перпендикулярна KD, то скорости точек С и D параллельны.

Рис. 8.12

Это означает, что третье звено находится в состоянии равных скоростей (не путать с мгновенным поступательным движением!). Скорости всех точек этого звена равны по величине и одинаково на­правлены.

Зная угловую скорость первого звена, находим скорость точки А

.

Угловая скорость второго звена

.

Скорость точки В

.

Так как КС=КВ, то скорость точки С равна скорости точки В по абсолютной величине.

Так как четвертое звено находится в состоянии равных скоро­стей, то скорости точек C,E и D равны.

Угловая скорость четвертого звена равна нулю. Угловая ско­рость пятого звена

.

Скорость точки F

.

Скорость точки М

.

Вычисления по указанным формулам приводят к ответу.

Ответ: v_B = 0,2 м/с; v_E = v_D = v_C=0,2 м/с; ω₂ = 1,3 рад/с;

ω₃ =0,5 рад/с; ω₄ =0; ω₅ =0,5 рад/с; v_F = 0,15 м/с; v_V=0,12 м/с.

Пример 5. Для механизма, кинематическая схема которого представлена на рис. 8.13, определить угловые скорости всех звень­ев и скорость точки М для заданного положения механизма. Разме­ры звеньев: ОА = 3,0 см; СВ = 3,2 см; BD = 1,2 см. Угловая скорость первого звена равна 2 рад/с.

Решение. Проанализируем движения звеньев данного механизма. Кривошип ОА вращается вокруг неподвижного центра О и приводит в движение шатун BD, который совершает сложное движение. Криво­шип ВС при этом вращается вокруг центра С, а ползун D движется поступательно прямолинейно по горизонтальной направляющей.

Очевидно, скорость точки А перпендикулярна ОА, скорость точ­ки В перпендикулярна ВС, а скорость точки D направлена горизон­тально (рис. 8.13).

Для определения скорости точки М необходимо знать угловую скорость этого звена и положение мгновенного центра скоростей.

Рис. 8.13

Определяем скорость точки А, которая принадлежит одновре­менно первому и третьему звену

.

Зная направления скоростей точек В и D, определяем положение МЦС второго звена, но для определения угловой скорости второго звена этого недостаточно. Ближайшим звеном к ведущему звену яв­ляется не второе, а третье звено, угловая скорость которого равна угловой скорости второго, так как третье звено относительно второ­го движется поступательно. Поэтому найдем угловую скорость третьего звена. Разложим движение этого звена на переносное вме­сте со вторым звеном и относительное относительно второго звена. Переносное движение третьего звена есть сложное движение, но в данный момент времени это есть мгновенное вращение вокруг цен­тра Р₂. Относительное движение есть поступательное прямолиней­ное вдоль прямой МА.

Найдем абсолютную скорость точки Р₂ третьего звена. По тео­реме сложения скоростей

.

Согласно определению переносная скорость точки равна абсо­лютной скорости соответствующей точки переносного тела. Точка Р₂ второго звена является его мгновенным центром скоростей, т.е. абсолютная скорость этой точки второго звена равна нулю и, следо­вательно, переносная скорость точки Р₂ третьего звена равна нулю и абсолютная скорость этой точки равна относительной.

На основании вышеизложенного МЦС третьего звена располо­жен на пересечении прямой ОА и перпендикуляра к прямой AM, проведенного через точку Р₂.

Далее, определяем угловую скорость третьего звена

.

Так как третье звено относительно второго движется поступа­тельно, то угловая скорость второго звена равна угловой скорости третьего звена.

Зная угловую скорость второго звена, находим скорость точки М

и скорость точки В

.

Далее, определяем угловую скорость четвертого звена

.

После измерений и вычислений получены следующие результаты:

АР₃ = 6,0; v_A = 6 см/с; ВР₂ = 6,4 см;

P₂D = 3,2 см; Р₂М=3,5 см;

ω₂ = ω₃ = 1 рад/с; v_B = 6,6 см/с; v_D = 3,5 см/с;

ω₄ = 1,2 рад/с; v_M = 3,20 см/с.

Пример 6. Для механизма, изображенного на рис. 8.14, найти МЦС третьего и четвертого звена.

Рис. 8.14

Решение. Для решения задачи применим метод остановки.

Остановим первое звено и найдем МЦС четвертого звена отно­сительно первого. Второе колесо при этом катится по первому как в планетарном механизме, т.е. искомый центр лежит на прямой ВК. Точка А в этом случае неподвижна, а скорость точки С относительно А перпендикулярна АС. Таким образом, МЦС четвертого звена от­носительно первого расположена в точке пересечения прямых ВК и АС, т.е. в точке Р₄₁, как это показано на рис. 8.14.

Так как точка О есть центр абсолютного вращения первого зве­на, то для четвертого звена это будет центр переносного вращения. Как известно, центры переносного, относительного и абсолютного вращений лежат на одной прямой, следовательно, МЦС четвертого звена в абсолютном движении лежит на прямой Р₄₁О. В то же время МЦС четвертого звена лежит на прямой О\В, так как абсолютная скорость точки В перпендикулярна О₁В. Таким образом, находим точку Р₄ Далее, находим скорость точки С и МЦС третьего звена.

Лекция 13

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

1 Абсолютное, переносное и относительное

движения точки

Сложное движение точки - это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движе­ниях. Например, сложное движение совершает лодка, переплываю­щая реку, пассажир, перемещающийся в вагоне движущегося поезда или по палубе плывущего парохода, а также человек, перемещающийся по лестнице движущегося эскалатора. Сложным является и движение шаров С и D центробежного регулятора Уатта (рис. 13.1), вращающегося вокруг вертикальной оси, когда при изменении нагрузки машины шары удаляются от этой оси или приближаются к ней, вращаясь со стерж­нями АС и BD вокруг шарниров А и В.

Рис. 13.1 Рис. 13.2

Рассмотрим движущееся тело А (рис. 13.2) и точку М, не принад­лежащую этому телу, а совершающую по отношению к нему некото­рое движение. Через произвольную точку О движущегося тела про­ведем неизменно связанные с этим телом оси x, у, z. Систему осей Охуz называют подвижной системой отсчета.

Неподвижной системой отсчета называют систему осей , связанную с некоторым условно неподвижным телом, обычно с Землей.

Движение точки М относительно неподвижной системы отсчета называют абсолютным движением точки.

Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозна­чают и .

Движение точки М относительно подвижной системы отсчета назы­вают относительным движением точки.

Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением точки и обо­значают и (relatif-относительный).

Движение подвижной системы отсчета Охуz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета является для точки М переносным движением. Точки тела А, совершая различные движения, имеют в данный момент различные скорости и ускорения. Скорость и ускорение точки тела А, связанного с под­вижной системой отсчета, совпадающей в данный момент с движу­щейся точкой, называют переносной скоростью и переносным ускоре­нием точки М и обозначают и (еmporter - увлекать).

Например, если человек идет вдоль радиуса вращающейся плат­формы (рис. 13.3), то с платформой можно связать подвижную систему отсчете, а с поверхностью Земли - неподвижную. Тогда движение платформы является переносным, движение человека по отношению к ней — относительным, а движение человека по отношению к Земле — абсолютным. Переносной скоростью человека , и его переносным ускорением являются скорость и ускорение той точки платформы, где находится в данный момент человек.

Рис. 13.3

Движение точки М (рис. 13.2) по отношению к неподвижной системе отсчета, которое названо абсолютным движением, является сложным, состоящим из относительного и переносного движений точки. Основная задача изучения сложного движения состоит в установле­нии зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движений точки.

Положение точки М относительно неподвижной системы отсчета определяется радиусом-вектором , проведенным в точку М из начала этой системы O₁. Изменение радиуса-вектора характеризует абсо­лютное движение точки. Положение точки М относительно подвиж­ной системы отсчета определяется радиусом-вектором , проведенным в точку М из начала этой системы О, или тремя координатами х, у, z в этой системе.

Изменение радиуса-вектора или координат х, у, z точки М характеризует относительное движение точки. Таким образом, уравнения относительного движения точки имеют вид

Изменение радиуса-вектора , проведенного из начала неподвиж­ной системы координат О₁ в полюс О, характеризует абсолютное движение полюса.