1.4. Путь при криволинейном движении

Е

Рис.1.6

сли известен вид функции , то может быть найден путь, пройденный точкой за определенный промежуток времени при произвольном движении по криволинейной траектории.

Пусть график зависимости от t представлен на рис.1.6. Разобьем промежуток времени () на N малых промежутков . За каждый такой промежуток, пройденный путь приближенно равен площади i-й полоски

, (1.24)

где - среднее значение скорости за данный промежуток времени.

Весь путь с момента t₁ до момента t₂ будет равен сумме

. (1.25)

В пределе при стремлении всех к нулю (одновременно число их растет) приближенное равенство станет точным

. (1.26)

Следовательно, путь, пройденный за время с момента t₁ до момента t₂ численно равен площади, ограниченной графиком функции , осью времени и прямыми t = t₁ и t = t₂ (см. рис.1.6).

Выражение (1.26) представляет собой определенный интеграл от функции , взятый в пределах от t₁ до t₂

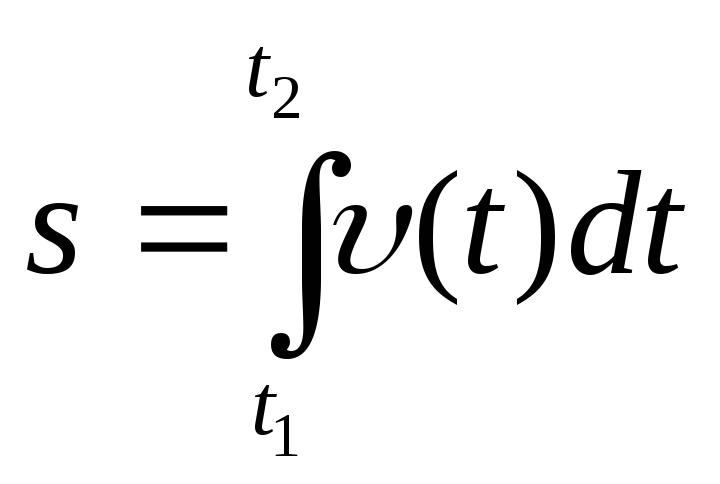. (1.27)

Таким образом, путь, пройденный телом за определенный промежуток времени, находится путем интегрирования функции в соответствующих пределах. Если же взять интеграл от вектора скорости, то получится вектор перемещения тела в интервале от t₁ до t₂

. (1.28)

С учетом (1.27), среднее значение величины скорости за время от t₁ до t₂ определяется выражением

. (1.29)

1.5. Частные случаи кинематики материальной точки

а) Равномерное прямолинейное движение

В случае движения точки вдоль положительного направления оси ОX

и .

Зависимость координаты x точки от времени найдем интегрированием

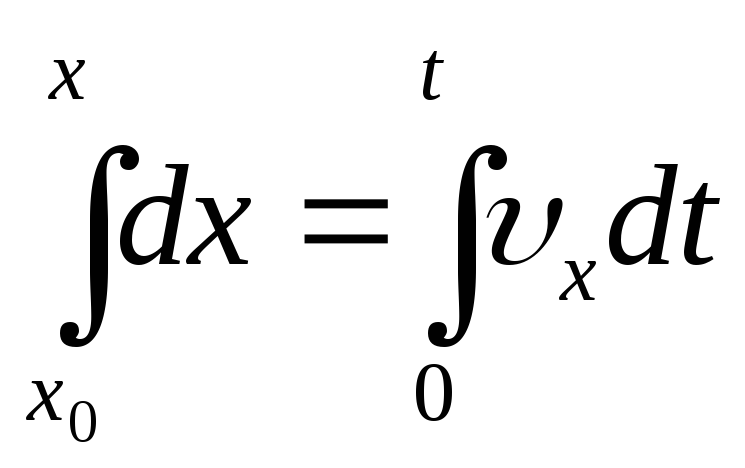, , , (1.30)

Рис. 1.7

где - координата точки в начальный момент времени.

Путь при равномерном прямолинейном движении

Графики пути и скорости равномерного прямолинейного движения представлены на рис. 1.7.

б) Равнопеременное прямолинейное движение

В этом случае . Если , то движение называют равноускоренным, а если - равнозамедленным. Ради простоты вместо пишут просто .

Зависимость величины скорости от времени имеет вид

, , (1.31)

где - скорость в начальный момент времени.

При движении вдоль положительного направления оси ОX координата изменяется по закону

, , (1.32)

а

Рис.1.8

уравнение пути

. (1.33)

Графики пути и скорости равнопеременного прямолинейного движения представлены на рис. 1.8.

в) Равномерное движение по окружности

В

Рис.1.9

еличина скорости остается неизменной (), но ее направление постоянно изменяется (), причем

.

Поместим начало системы координат в центр окружности, по которой движется точка, и пусть в начальный момент времени она находилась в наивысшей точке А (рис.1.9). Обозначим меняющийся со временем угол между и OY через . Тогда кинематические уравнения движения будут иметь вид

,

а уравнение траектории .

г) Движение тела, брошенного под углом к горизонту

Пусть тело брошено под углом α к горизонту со скоростью (рис.1.10). У поверхности Земли и без учета сопротивления воздуха его ускорение равно ускорению свободного падения g=9,81 м/с².

В выбранной декартовой системе координат вектор скорости и радиус-вектор меняются по закону

Рис.1.10

, (1.34)

. (1.35)

В соответствии с принципом независимости движений это движение можно разложить вдоль координатных осей на два прямолинейных. Движение тела вдоль оси OX будет равномерным (g_x=0), а вдоль оси OY равнопеременным (g_y=-g), при этом проекции начальной скорости равны

(1.36)

Проектируя уравнения (1.34) и (1.35) на оси координат, получим следующую систему уравнений

Решение данной системы уравнений позволяет определить время полета, максимальную высоту подъема и дальность полета.

В наивысшей точке подъема вертикальная составляющая скорости , следовательно, время подъема , а высота подъема над горизонтом в этот момент .

В момент времени тело упадет на землю, пройдя вдоль оси Oх расстояние При заданной начальной скорости максимальная дальность полета достигается при, то есть при.

Решая систему кинематических уравнений, получим уравнение траектории движения тела

. (1.37)

Нетрудно видеть, что данное уравнение представляет собой параболу (см. рис.1.10). Радиус кривизны данной траектории в любой ее точке можно определить, используя формулу нормального ускорения (1.21). Так, в наивысшей точке траектории , а , отсюда

. (1.38)