1.3. Ускорение

Рис. 1.3

При движении точки по криволинейной траектории величина и направление скорости могут изменяться. Быстроту изменения вектора скорости с течением времени характеризует ускорение.

Рассмотрим движение материальной точки по некоторой кривой (1.3). Пусть в некоторый момент времени t₁ точка имела скорость , а в момент времени t₂ - скорость . Векторхарактеризует изменение скорости за время как по величине, так и по направлению. Для его построения перенесем вектор параллельно самому себе так, чтобы его начало совместилось с началом вектора . В этом случае вектор, соединяющий конец с концом и будет представлять собой вектор . Отношение изменения скорости к тому промежутку времени , в течение которого это изменение произошло, выражает вектор среднего ускорения за этот промежуток времени

. (1.12)

Мгновенным ускорением или ускорением точки в данный момент времени t называют величину, математически определяемую как

(1.13)

Таким образом, вектор ускорения в любой момент времени равен первой производной по времени от вектора скорости, или второй производной от радиус-вектора. Численное значение ускорения можно рассчитать через вторую производную от пути по времени

. (1.14)

Вектор ускорения можно представить в виде векторной суммы его составляющих по осям координат

. (1.15)

В то же время, дифференцируя вектор скорости по времени, получаем

. (1.16)

Из сопоставления (1.15) и (1.16) следует, что проекции вектора ускорения на координатные оси равны первым производным соответствующих проекций скорости или вторым производным соответствующих координат по времени. Величина ускорения в этом случае равна

. (1.17)

В

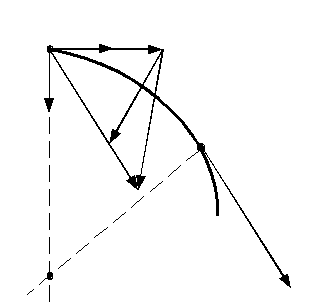Рис.1.4

ектор ускорения, характеризующий быстроту изменения скорости как по величине, так и по направлению, целесообразно разложить на две составляющие так, чтобы одна из них характеризовала только изменение величины скорости, а другая – только ее направление. С этой целью представим приращение вектора скорости в виде суммы двух векторов (рис.1.4)

. (1.18)

При построении мы отложили отрезок АС=АD, в результате чего, вектор характеризует изменение скорости по величине, вектор - ее изменение по направлению. Проведем также к векторам и линии нормали, которые пересекутся в некоторой точке О, называемой центром кривизны траектории АВ. При приближении точки В к точке А расстояния R₁ и R₂ стремятся к некоторой величине R, которая называется радиусом кривизны траектории в точке А.

Разделив обе части выражения (1.18) на и перейдя к пределу, получим

. (1.19)

Первое слагаемое в правой части представляет ускорение, которое характеризует только изменение скорости по величине, оно называется тангенциальным ускорением. Второе слагаемое характеризует только изменение направления скорости и называется нормальным ускорением.

Можно показать, что

, (1.20)

где - единичный вектор, направленный по касательной к траектории в рассматриваемой точке (тангенциальный – означает касательный: отсюда – название ускорения). А также

, (1.21)

где - единичный вектор нормали к мгновенной скорости в рассматриваемой точке траектории, отсюда название – нормальное ускорение; R – радиус кривизны траектории в данной точке.

Таким образом, тангенциальное и нормальное ускорения представляют собой две взаимно перпендикулярные составляющие полного ускорения, а следовательно,

. (1.22)

Н

Рис.1.5

а рис.1.5 показаны векторы тангенциального, нормального и полного ускорений для частного случая движения точки А по криволинейной траектории. Направление полного ускорения можно определить углом φ между векторами и :

. (1.23)