6. Неинерциальные системы отсчета. Силы инерции
Законы динамики выполняются в инерциальных системах отсчета. Поставим теперь задачу найти уравнения движения в неинерциальных системах отсчета, т.е. таких системах, которые движутся ускоренно относительно инерциальных систем. В классической физике эту задачу решают введением в неинерциальные системы отсчета сил инерции, возникновение которых обусловлено ускоренным движением этих систем. При этом силы инерции вводят таким образом, чтобы уравнения движения имели такой же вид, как и в инерциальной системе отсчета.
6.1. Силы инерции при ускоренном поступательном движении системы отсчета
Рис.6.1
Рассмотрим вначале неинерциальную
систему отсчета
,
движущуюся поступательно с ускорением
относительно инерциальной системы
отсчета К (рис.6.1). Радиус-векторы
материальной точки М в данных системах
отсчета связаны между собой соотношением
,
(6.1)
где
- вектор, соединяющий начала координат
инерциальной и неинерциальной систем
отсчета.
Продифференцировав это соотношение дважды по времени, получим
,
(6.2)
где
-
ускорение точки в инерциальной системе
К,
-
ускорение в неинерциальной системе К’.
Умножив данное равенство на массу материальной точки, приведем его к виду
.
(6.3)
Здесь
- есть результирующая всех реально
действующих сил, вызывающая ускоренное
движение в К-системе. Величина
имеет размерность силы и называется
силой инерции. Она возникает не из-за
взаимодействия тел, а из-за ускоренного
движения системы отсчета. С учетом этого
основное уравнение динамики для
материальной точки в неинерциальной
системе отсчета принимает вид
.
(6.4)
Таким образом, введение силы инерции в неинерциальной системе координат позволяет сохранить для таких систем обычную форму записи уравнений движения, но в этом случае к сумме сил, действующих на тело со стороны других тел, следует добавить силу инерции.
Силы инерции реально действуют на тела в неинерциальной системе отсчета и могут быть измерены. Однако, в отличие от «обычных» сил, для сил инерции нельзя указать, действие каких тел они выражают. Следовательно, к этим силам не применим 3-ий закон Ньютона. Кроме того, в неинерциальной системе отсчета невозможно выделить замкнутую систему тел, так как силы инерции ко всем телам системы будут внешними. Поэтому, в неинерциальной системе отсчета не выполняются законы сохранения импульса и энергии.
В заключение отметим, что как силы тяготения, так и силы инерции сообщают телам одинаковые ускорения, независимо от их массы. Поэтому, действие на тело силы инерции можно заменить действием эквивалентного поля тяготения. Этот принцип получил название принципа эквивалентности и состоит в следующем: движение тела по отношению к неинерциальной системе отсчета эквивалентно его движению относительно инерциальной системы, совершающемуся под действием всех реально взаимодействующих с ним тел, а также некоторого дополнительного поля тяготения.
6.2. Силы инерции во вращающейся системе отсчета
Рис.6.2
Рассмотрим теперь поведение тел в
неинерциальной системе отсчета,
вращающейся относительно инерциальной
системы с постоянной угловой скоростью.
Такой системой, например, может быть
диск, вращающийся вокруг перпендикулярной
к нему оси с угловой скоростью
(рис.6.2).
Допустим, что по окружности радиуса
равномерно
движется, привязанный нитью к оси диска,
шарик со скоростью
относительно
диска, т.е. неинерциальной системы
отсчета. Скорость шарика относительно
инерциальной системы будет равна
.
(6.5)
Знак в этой формуле зависит от направления движения шарика.
Ускорение шарика в неподвижной системе определяется выражением
,
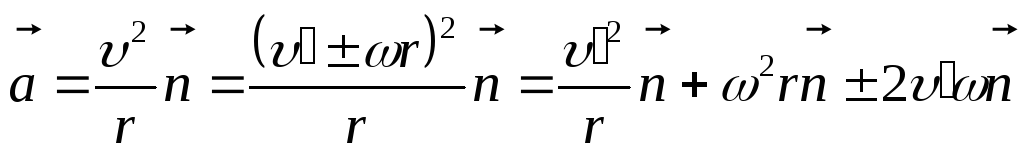где
- единичный вектор, направленный к
центру окружности.
В полученном выражении величина
представляет собой ускорение шарика
относительно диска, т.е. вращающейся
системы
,
а произведение
дает силу натяжения нити. Следовательно,
основной закон динамики во вращающейся
системе отсчета можно написать следующим
образом
.
(6.6)
Таким образом, во вращающейся неинерциальной
системе
кроме реальной силы
,
обусловленной натяжением нити, действуют
еще две дополнительные силы. Первая из
них, определяемая выражением
,
(6.7)
называется центробежной силой инерции. Эта сила направлена вдоль радиуса от оси вращения. Она действует во вращающихся системах отсчета на все тела, независимо от того, покоится тело в этих системах отсчета или движется.
Вторая сила, называемая силой Кориолиса, в векторной форме может быть представлена в виде
.
( 6.8)
Действительно, модуль векторного
произведения
равен
,
так как угол между данными векторами
равен
,
а его направление совпадает или
противоположно с
.
На основании анализа формулы (6.8) можно сделать следующие выводы:
- сила Кориолиса действует только на движущиеся тела во вращающейся системе отсчета;
- сила Кориолиса перпендикулярна вектору
,
поэтому всегда лежит в плоскости,
перпендикулярной оси вращения;
- сила Кориолиса перпендикулярна вектору
скорости
и
не совершает работы над движущимся
телом; эта сила может изменить только
направление скорости, но не ее модуль.
Любая система отсчета, связанная с Землей, является неинерциальной системой. Вращение Земли приводит к действию как центробежной, так и кориолисовой сил. Векторная сумма силы гравитационного притяжения Земли и центробежной силы инерции рассматривается как единая величина, называемая силой тяжести
.
(6.9)
Рис.6.3
и
(рис.6.3).
Таким образом, направление к центру
Земли не совпадает с направлением
отвеса, хотя ввиду медленности вращения
Земли оба направления отличаются друг
от друга незначительно.
Более существенно влияет на характер движения тел кориолисова сила. Так, при свободном падении тел происходит их отклонение к востоку от линии подвеса. Этот эффект максимален на экваторе и отсутствует на полюсе. Для широты Москвы при падении с высоты 100 м это отклонение составляет 1,2 см. Действие силы Кориолиса приводит также к отклонению движущихся вдоль меридиана тел к востоку в северном полушарии и к западу в южном. Именно этим объясняется то, что реки северного полушария, текущие в меридианальном направлении, подмывают всегда правый берег.