1.2. Скорость

Р

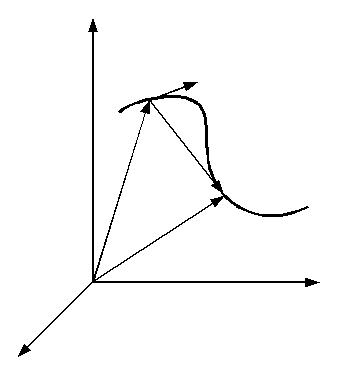Рис.1.2

ассмотрим движение точки по произвольной криволинейной траектории (рис.1.2). Пусть в момент времени t₁ она занимала положение А, определяемое радиус-вектором , а в момент времени t₂ – положение В, определяемое радиус-вектором . Вектор , проведенный из начальной точки А в конечную В, характеризует изменение пространственного положения точки за данный промежуток времени и называется вектором перемещения. Отрезок траектории , заключенный между точками А и В, называется путем, пройденным за тот же промежуток времени . В общем случае путь отличен по величине от модуля вектора перемещения , однако это различие будет тем меньше, чем меньше . Если устремить к нулю, то , т.е. для бесконечно малого перемещения справедливо равенство .

Для характеристики направления и быстроты движения материальной точки вводится понятие скорости. Введем вначале понятие вектора средней скорости. Отношение вектора перемещения за некоторый интервал времени к его величине называется вектором средней скорости за данное время

. (1.4΄)

Вектор направлен так же, как, т.е. вдоль хорды АВ. Если промежуток времени уменьшать, то при достижении им достаточно малых значений вектор практически перестанет изменяться как по величине, так и по направлению. Это означает, что при отношение (1.4΄) стремится к некоторому пределу, определяющему вектор скорости в момент времени t :

. (1.5)

Таким образом, вектор скорости материальной точки в данный момент времени есть первая производная ее радиус-вектора по времени. Вектор скорости в любой точке траектории направлен по касательной к траектории точки в сторону ее движения.

Модуль вектора скорости равен

, (1.6)

т.е. величина скорости в данный момент времени равна производной пути по времени.

Вектор скорости, как и всякий другой вектор, можно разложить на его составляющие по осям координат

. (1.7)

С другой стороны

. (1.8)

Из сравнения (1.6) и (1.7) следует, что

, (1.9)

т.е. проекции вектора скорости на координатные оси равны производным по времени соответствующих координат точки. При этом численное значение скорости можно представить также в виде

. (1.10)

В соответствии с экспериментальным принципом независимости движений, если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых за то же время в каждом из движений порознь. Такой же вывод можно сделать и для скорости движения, получивший название закона сложения скоростей

, (1.11)

где - скорость материальной точки при i-м независимом движении, n – число таких движений.

Таким образом, при трехмерном (или двухмерном) движении мы можем рассматривать перемещение и скорость точки в направлении любой оси координат независимо от того, как она движется относительно других осей.