Скалярное и векторное произведение векторов

Скалярным произведением векторов и называется скаляр, равный произведению модулей этих векторов на косинус угла между ними

.

Скалярное произведение обращается в нуль, если один из сомножителей есть нуль-вектор, или если векторы и перпендикулярны.

Скалярный квадрат вектора есть квадрат его модуля.

.

Скалярного куба (и тем более высших степеней) в векторной алгебре нет.

Скалярное произведение коммутативно, т.е. не зависит от порядка сомножителей

,

и дистрибутивно, т.е. произведение вектора на сумму нескольких векторов равно сумме произведений вектора на каждый из складываемых векторов, взятый в отдельности.

В

Рис.П1.8

декартовой системе координат выражение скалярного произведения через координаты сомножителей имеет вид

.

Векторным произведением вектора на не коллинеарный (не параллельный) ему вектор называется третий вектор , который строится следующим образом (рис.П1.8):

1. его модуль численно равен площади параллелограмма, построенного на векторах и , т.е. он равен ;

2. его направление перпендикулярно плоскости упомянутого параллелограмма;

3. при этом направление вектора выбирается так, чтобы векторы составляли правовинтовую систему, т.е. его направление связано с направлением вращения от первого сомножителя ко второму правилом винта

Обозначение векторного произведения:

или .

Векторное произведение дистрибутивно, но не обладает свойством коммутативности. Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное

.

В декартовой системе векторное произведение можно представить в виде определителя

.

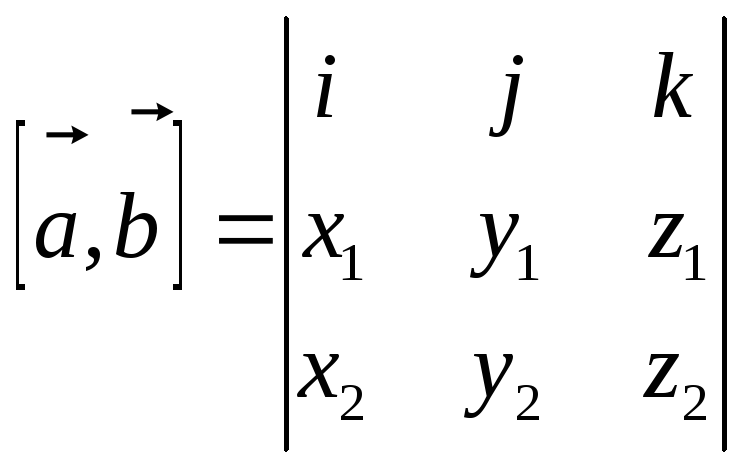Смешанным (или векторно-скалярным) произведением трех векторов(взятых в указанном порядке) называется скалярное произведение вектора на векторное произведение , т.е. число , или, что то же . Обозначение: .

Смешанное произведение векторов равно объему параллелепипеда, построенного на этих векторах.

При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный:

.

Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю

.

Выражение смешанного произведения через координаты сомножителей

.

Двойным векторным произведением называется выражение

.^

Производная и дифференциал

Предел, к которому стремится отношение бесконечно малого приращения функции к бесконечно малому приращению аргумента , называется производной и обозначается следующим образом

Рис.П1.9

.

Производная численно равна тангенсу угла наклона касательной к кривой в точке (рис.П1.9) Если , то при увеличении функция возрастает, если то при возрастании функция уменьшается.

В физике принято производные по времени обозначать символом соответствующей величины с точкой над ним, например,

, .

Дифференциалом функции называется произведение производной на приращение аргумента:

,

где - производная по .

Производную функции y по аргументу x бывает удобно обозначать через дифференциалы

.

Производная сложной функции равна производной по вспомогательной переменной, умноженной на производную этой переменной по аргументу

.

Дифференциал произведение двух функций равен сумме произведений каждой функции на дифференциал другой

.

Дифференцировал дроби:

.

Полный дифференциал функции нескольких переменных определяется по формуле

,

где - частные производные функции по соответствующим переменным. Для нахождения частной производной, например , достаточно найти обыкновенную производную переменной f, считая последнюю функцией одного аргумента x.

Таблица П1.1