4.8. Потенциальные кривые. Условия равновесия механической системы

П

Рис.4.9

отенциальной кривой называют график зависимости потенциальной энергии тела, находящегося в силовом поле, от координат. В некоторых простейших случаях, потенциальная энергия зависит только от одной координаты. Одним из таких примеров является тело, совершающее колебания в горизонтальной плоскости под действием упругих сил пружин. Другим примером может служить тело, находящееся в поле силы тяжести и скользящее без трения по изогнутой в вертикальной плоскости проволоке. Графики потенциальных кривых для данных случаев представлены на рис.4.9 и рис.4.10.

По графику потенциальной кривой легко сделать ряд заключений о характере движения тела и условии его равновесия. Поясним это, используя зависимость на рис.4.10.

Рис.4.10

Рассматриваемая система является замкнутой и консервативной, поэтому ее полная механическая энергия сохраняется, т.е. . Из этого следует, что кинетическая энергия системы может возрастать только за счет уменьшения потенциальной энергии. В состоянии, когда , а , система не может прийти в движение без воздействия извне, т.е. будет находиться в равновесии. Условие минимума потенциальной энергии имеет вид

. (4.36)

Данное условие выполняется при и соответствует состоянию устойчивого равновесия.

При

(4.37)

функция имеет в точке максимум, что соответствует состоянию неустойчивого равновесия.

Если полная энергия имеет значение Е, указанное на рис., то тело может совершать движение либо от x₁ до x₂ , либо в пределах от x₃ до бесконечности. В области x<x₁ и x₂<x<x₃ тело проникнуть не может, так как потенциальная энергия не может стать больше полной энергии. Таким образом, область x₂<x<x₃ представляет собой потенциальный барьер, через который тело проникнуть не может, имея данный запас энергии. Область x₁<x<x₂ называется потенциальной ямой.

В заключение отметим, что во многих разделах физики возникает необходимость в построении и анализе потенциальных кривых.

4.9. Примеры решения задач

1. Сила, действующая на частицу, имеет вид , где и b – константы. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (3,4,5) м.

Решение

Элементарная работа согласно определению

.

Полную работу найдем путем интегрирования

.

Как следует из условия задачи, проекции силы на соответствующие координатные оси равны , , а , .

С учетом этого, окончательно имеем

.

2. Тело массы m начинает двигаться под действием силы . Найти мощность , развиваемую силой в момент времени t.

Решение

По определению мгновенная мощность

.

Вектор скорости тела к моменту времени найдем путем интегрирования ускорения по времени

.

Вектор ускорения выразим из второго закона Ньютона

.

Подставляя найденное выражение в формулу для вектора скорости, имеем

.

С учетом полученного выражения мощность, развиваемая телом к моменту времени t равна

.

3. Потенциальная энергия частицы имеет вид , где r – модуль радиус-вектора частицы, - константа. Найти силу , действующую на частицу, и работу, совершаемую над частицей при переходе ее из точки М(1,2,3) в точку N(2,3,4).

Решение

Вектор силы градиенту потенциальной энергии с обратным знаком

, .

Учитывая, что =а, частные производные потенциальной энергии по координатам будут равны

, , .

Тогда вектор силы действующей на частицу

,

где .

Работа, совершаемая над частицей при переходе ее из точки М(1,2,3) в точку N(2,3,4) равна убыли потенциальной энергии, т.е.

=

.

4. Какова минимальная работа, которую надо затратить, чтобы втащить волоком тело массы m на горку длины L и высоты H ? Коэффициент трения равен .

Решение

Чтобы втащить волоком тело массы m на горку длины L и высоты H, необходимо совершить работу против силы тяжести и силы трения. Следовательно

.

По определению эти работы соответственно равны

, .

После подстановки, получим

,

где

.

5. Частица массы m₁ испытывает упругое центральное столкновение с неподвижной частицей массы m₂. Какую долю своей энергии первая частица передала второй?

Решение

Доля энергии, переданная первой частицей при столкновении со второй, выразится соотношением:

,

где - кинетическая энергия первой частицы до столкновения, - приобретенная кинетическая энергия второй частицы.

При упругом столкновении выполняются законы механической энергии и сохранения импульса. Применяя эти законы, получим следующую систему

,

где и - скорости первой частицы до и после столкновения соответственно, - скорость второй частицы после столкновения.

Решая совместно уравнения, найдем

.

С учетом полученного выражения доля энергии, переданная первой частицей при столкновении со второй, будет равна

.
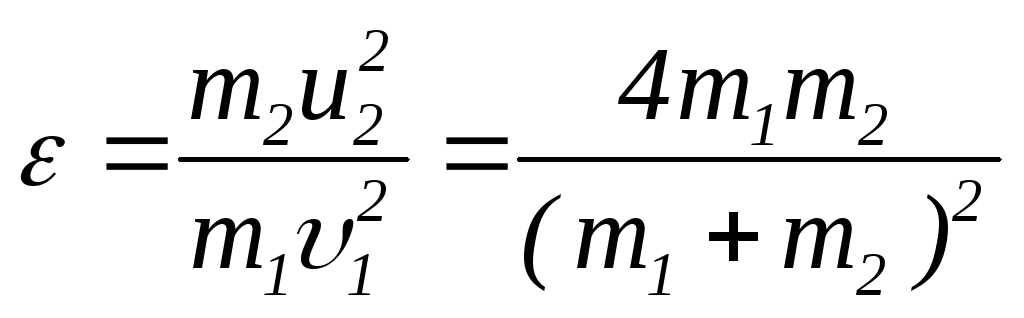